
- •Йошкар-Ола
- •Рецензенты:
- •Содержание
- •Предисловие
- •Правила техники безопасности при выполнении лабораторных работ при работе на персональном компьютере
- •Запрещается:
- •Свойства обратной матрицы
- •Варианты заданий.
- •Образец выполнения задания №1
- •Задание №2.Используя метод Гаусса, решить систему уравнений с точностью до 0,001. Теоретическая часть.
- •Варианты заданий
- •Образец выполнения задания №2
- •Варианты заданий
- •Образец выполнения задания
- •Пример решения системы нелинейных уравнений методом итераций
- •Пример решения системы нелинейных уравнений методом Ньютона
- •Контрольные вопросы
- •Лабораторная работа №3 Численное дифференцирование и интегрирование в математическом моделировании, вычисление интегралов методом прямоугольников.
- •Теоретическая часть.
- •Образец выполнения задания.
- •Пример вычисления интегралов методом левых и правых прямоугольников
- •Пример вычисления интегралов методом средних прямоугольников
- •Метод парабол (метод Симпсона)
- •Увеличение точности
- •Варианты заданий
- •Контрольные вопросы
- •Лабораторная работа № 5. Приближенные методы решения обыкновенных дифференциальных уравнений. Метод конечных разностей.
- •Теоретическая часть.
- •Варианты заданий
- •Образец выполнения задания
- •Заключение
- •Список литературы
Варианты заданий
№1. 1) 2)
2)
№2. 1) 2)
2)

№3. 1)
 2)
2)

№4. 1)
 2)
2)

№5. 1)
 2)
2)

№6. 1)
 2)
2)

№7. 1)
 2)
2)

№8. 1)
 2)
2)

№9. 1)
 2)
2)

№10.1)
 2)
2)

№11.1)
 2)
2)

№12.1)
 2)
2)
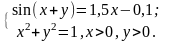
№13.1)
 2)
2)
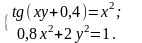
№14.1)
 2)
2)

№15.1)
 2)
2)

№16.1)
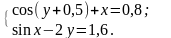 2)
2)

№17.1)
 2)
2)

№18.1)
 2)
2)

№19.1)
 2)
2)

№20.1) 2)
2)
№21. 1)
 2)
2)

№22. 1)
 2)
2)

№23. 1)
 2)
2)

№24. 1)
 2)
2)

№25. 1)
 2)
2)

№26. 1)
 2)
2)

№27. 1)
 2)
2)

№28. 1)
 2)
2)

№29. 1)
 2)
2)

№30. 1)
 2)
2)

Образец выполнения задания
№1. 1)
 2)
2)

Пример решения системы нелинейных уравнений методом итераций
Перепишем данную систему в виде:

Отделение корней производим графически (рис.1). Из графика видим, что система имеет одно решение, заключенное в области D:0<х<0,3;-2,2<y<-1,8.
Убедимся в том, что метод итераций применим для уточнения решения системы, для чего запишем ее в следующем виде:

Так
как ,то
имеем в области D
,то
имеем в области D
 +
+ =
= ;
;
+
=
Таким образом, условия сходимости выполняются.

Рис.1
Таблица №2
-
п






0
0,15
-2
-0,45
-0,4350
-0,4161
-0,1384
1
0,1616
-2,035
-0,4384
-0,4245
-0,4477
-0,1492
2
0,1508
-2.0245
-0,4492
-0,4342
-0,4382
-0,1461
3
0.1539
-2,0342.
-0,4461
-0.4313
-0,4470
-0,1490
4
0.1510
-2,0313
-0,4490
-0,4341
-0,4444
-0.1481
5
0,1519
-2,0341
-0,4481
-0,4333
-0,4469
-0,1490
6
0,1510
-2.0333
-0.449
-0,4341
-0.4462
-0,1487
7
0.1513
-2.0341
-0,4487
-0,4340
-0,4469
-0.1490
8
0.1510
-2,0340

За начальные приближения принимаем хо=0,15, у0 = -2.
(таб.№2).
Тогда ответ
запишется:

Пример решения системы нелинейных уравнений методом Ньютона
Отделение корней
производим графически (рис.2).
Для построения графиков
функций составим
таблицу значений функций
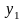 и
и
 ,
входящих в первое и второе уравнения
(табл. I).
,
входящих в первое и второе уравнения
(табл. I).

Рис.2
Значения
для x
можно брать исходя из следующих условий:
из первого уравнения
 1≤1,2х+0,4≤1,
т.е.
1,16≤х≤0,5;
из второго уравнения
1≤1,2х+0,4≤1,
т.е.
1,16≤х≤0,5;
из второго уравнения
 ,
т.е.
,
т.е.
 . Таким образом,
. Таким образом,
 .
.
Система имеет два решения. Уточним одно из них, принадлежащее области D: 0,4<x<0,5;
0,76<y<0,73.
За начальное приближение примем
 Имеем:
Имеем:



Таблица №3
x |
-1,1 |
-1 |
-0,8 |
-0,6 |
-0,2 |
-0,4 |
0 |
0,2 |
0,4 |
0,5 |
х2 |
1.21 |
1 |
0,64 |
0,36 |
0,04 |
0,16 |
0 |
0,04 |
0.16 |
0,25 |
0,8 х2 |
0,97 |
0,8 |
0,51 |
0,29 |
0,032 |
0,13 |
0 |
0,032 |
0,13 |
0,2 |
1 -0,8 х2 |
0,03 |
0,2 |
0,49 |
0,71 |
0,97 |
0,87 |
1 |
0,97 |
0.87 |
0,8 |
|
0,02 |
0,13 |
0,33 |
0,47 |
0,65 |
0,58 |
0,67 |
0,65 |
0,58 |
0.53 |
|
±0,14 |
±0,36 |
±0,57 |
±0,69 |
±0,81 |
±0,76 |
±0,82 |
±0.81 |
±0,76 |
±0.73 |
1,2x |
-1,32 |
-1,2 |
-0,9б' |
-0,72 |
-0,24 |
-0,48 |
0 |
0,24 |
0,48 |
0,6 |
0,4+1,2x |
-0,92 |
-0,8 |
-0,56 |
-0,32 |
0,16 |
-0,08 |
0,4 |
0,64 |
0.88 |
1 |
2x-y |
-1.17 |
-0,93 |
-0,59 |
-0,33 |
0,16 |
-0,08 |
0,41 |
0,69 |
2.06 1,08 |
1,57 |
|
-1,03 |
-1,07 |
-1,01 |
-0,87 |
-0,56 |
-0,72 |
-0,41 |
-0,29 |
-1,26 -1,28 |
-0.57 |
Уточнение корней проводим методом Ньютона:

где ;
;
 ;
;

 ;
; ;
;

Все вычисления производим по таблице 3
Таблица 3 |
|
|
0,10 |
0,017 |
-0,0060 |
0,0247 |
-0,0027 |
-0,0256 |
0,0001 |
0,0004 |
|
|
|
|||||||
|
|
0,2701 |
0,0440 |
-0,0193 |
0,0794 |
-0,0080 |
-0,0764 |
-0,0003 |
0,0013 |
|
|
|
||||||||
|
|
2,6197 |
3,2199 |
2,9827 |
3,1673 |
|
|
|
||||||||||||
|
|
-0,0208 |
-2,25 |
0,1615 |
-2,199 |
0,1251 |
-2,1249 |
0,1452 |
-2,2017 |
|
|
|
||||||||
|
|
-1,1584 |
0,64 |
-1,523 |
0,8 |
-1,4502 |
0,7904 |
-1,4904 |
0,7861 |
|
|
|
||||||||
|
|
0,1198 |
-0,0282 |
-0,0131 |
0,059 |
-0,0007 |
-0,0523 |
-0,0002 |
0,0010 |
|
|
|
||||||||
|
|
0,9988 |
0,0208 |
0,9869 |
-0,1615 |
0,9921 |
-0,1251 |
-0,9894 |
-0,1452 |
|
|
|
||||||||
|
0,55 |
0,733 |
1,6963 |
1,7165 |
|
|
|
|||||||||||||
|
|
0,128 |
0,8438 |
0,2 |
0,8059 |
0,1952 |
0,7525 |
0,1931 |
0,8079 |
|
|
|
||||||||
|
|
0,4 |
0,75 |
0,50 |
-0,733 |
0,4940 |
-0,7083 |
0,4913 |
-0,7339 |
0,4912 |
-0,7335 |
Ответ: x≈0,491 y≈ 0,734 |
||||||||
n |
0 |
1 |
2 |
3 |
4 |
|
||||||||||||||



















