Образец выполнения задания №1

1)∆= = =

=-(105+16+56-98+10+96)=-185;

= = =

=-(-33+234-35+91-22+135)=-370;

= = =

=-(360-91-700+36-700+910)=185;

= = =

=-(75-44+728-70+130-264)=-555

= = =

=-(455-40+88-154+416-25)=-740;

= = =2; = = =-1;

= = =3; = = =4;

Ответ:

2) = ;

∆= =24-24-15-27+16+20=-6;

= ;

;

Ответ:

3) 3A+B= ;

2A-B= ;

(3A+B)*(2A-B)= .

1. Имеем AX=B, откуда X= B. Находим

∆=

= ;

=

= .

Задание №2.Используя метод Гаусса, решить систему уравнений с точностью до 0,001. Теоретическая часть.

Метод Гаусса — классический метод решения системы линейных алгебраических уравнений. Это метод последовательного исключения переменных, когда с помощью элементарных преобразований система уравнений приводится к равносильной системе ступенчатого (или треугольного) вида, из которой последовательно, начиная с последних (по номеру) переменных, находятся все остальные переменные

Описание метода.

Пусть исходная система выглядит следующим образом

, (1)

Матрица A называется основной матрицей системы, b — столбцом свободных членов.

Тогда согласно свойству элементарных преобразований над строками основную матрицу этой системы можно привести к ступенчатому виду(эти же преобразования нужно применять к столбцу свободных членов):

При этом будем считать, что базисный минор (ненулевой минор максимального порядка) основной матрицы находится в верхнем левом углу, то есть в него входят только коэффициенты при переменных x_j1, …, x_jr.

Тогда переменные x_j1, …, x_jr называются главными переменными. Все остальные называются свободными.

Если хотя бы одно число β_i≠0, где i>r , то рассматриваемая система несовместна, т.е. у неё нет ни одного решения.

Пусть β_i=0 для любых i>r.

Перенесём свободные переменные за знаки равенств и поделим каждое из уравнений системы на свой коэффициент при самом левом где   — номер строки):

, где i=1, … , r, k=i+1, … , n.

Если свободным переменным системы (2) придавать все возможные значения и решать новую систему относительно главных неизвестных снизу вверх (то есть от нижнего уравнения к верхнему), то мы получим все решения этой СЛАУ. Так как эта система получена путём элементарных преобразований над исходной системой (1), то по теореме об эквивалентности при элементарных преобразованиях системы (1) и (2) эквивалентны, то есть множества их решений совпадают.

Варианты заданий

№1. .

№2.

№3.

№4.

№5.

№6.

№7.

№8.

№9.

№10.

№11.

№12.

№13.

№14.

№15.

№16.

№17.

№18.

№19.

№20.

№21.

№22.

№23.

№24.

№25.

№26.

№27.

№ 29.

№30.

Образец выполнения задания №2

Вычисления производим по схеме единственного деления представленного в таблице №1.

Таблица №1

Коэффициенты при неизвестных				Свободные члены		Контрольные суммы ∑		Строчные Суммы ∑’
0,68	0,05	-0,11	0,08	2,15	2,85		2,85
0,21	-0,13	0,27	-0,8	0,44	-0,01		-0,01
-0,11	-0,84	0,28	0,06	-0,83	-1,44		-1,44
-0,08	0,15	-0,5	-0,12	1,16	0,61		0,61
1	0,0735	-0,0618	0,1176	3,1618	4,1912		4,1912
	-0,1454	0,30398	-0,8242	-0,22398	-0,89015		-0,8901
	-0,8319	0,2622	0,0729	-0,4822	-0,97897		-0,97896
	0,1559	-0,5129	-0,1106	1,4129	0,9453		0,9453
	1	-2,0906	5,6719	1,5404	6,1221		6,1217
		-1,47697	4,79139	0,7992	4,1140		4,1136
		-0,18697	-0,9948	1,1723	-0,00913		-0,0095
		1	-3,2441	-0,5411	-2,7854		-2,7851
			-1,6013	1,0711	-0,5299		-0,5302
			1	-0,6689	0,3309		0,3311
2,8264	-0,3337	-2,7110	-0,6689
3,8263	0,6664	-1,7119	0,3309

Ответ:

Контрольные вопросы

1). Привести общий вид системы линейных алгебраических уравнений.

2). Дать определение обратной матрицей.

3).Перечислить свойства обратной матрицы.

4). Описать метод Крамера.

5). Дать определение ранга матрицы.

6). Объяснить соотношение между числом неизвестных решений и рангом системы.

Лабораторная работа № 2

Методы решения систем нелинейных уравнений

Задание:

1. Используя метод итераций, решить систему

нелинейных уравнений с точностью до 0,001.

2) Используя метод Ньютона, решить систему

нелинейных уравнений с точностью до 0,001.

Задание №1Используя метод итераций, решить систему нелинейных уравнений с точностью до 0,001.

Теоретическая часть.

Метод итераций это способ численного решения математических задач. Его суть – нахождение алгоритма поиска по известному приближению (приближенному значению) искомой величины следующего, более точного приближения. Применяется в случае, когда последовательность приближений по указанному алгоритму сходится.

Данный метод называют также методом последовательных приближений, методом повторных подстановок, методом простых итераций и т.п.

Метод Ньютона, алгоритм Ньютона (также известный как метод касательных) — это итерационный численный метод нахождения корня (нуля) заданной функции. Метод был впервые предложен английским физиком, математиком и астрономом Исааком Ньютоном (1643—1727). Поиск решения осуществляется путём построения последовательных приближений и основан на принципах простой итерации. Метод обладает квадратичной сходимостью. Улучшением метода является метод хорд и касательных. Также метод Ньютона может быть использован для решения задач оптимизации, в которых требуется определить нуль первой производной либо градиента в случае многомерного пространства. Обоснование

Чтобы численно решить уравнение методом простой итерации, его необходимо привести к следующей форме: , где - сжимающее отображение.

Для наилучшей сходимости метода в точке очередного приближения должно выполняться условие . Решение данного уравнения ищут в виде , тогда:

В предположении, что точка приближения «достаточно близка» к корню , и что заданная функция непрерывна , окончательная формула для такова:

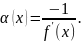
С учётом этого функция определяется выражением:

Эта функция в окрестности корня осуществляет сжимающее отображение[1], и алгоритм нахождения численного решения уравнения сводится к итерационной процедуре вычисления:

.