Практическое занятие №30

Наименование занятия: Нахождение первообразной. Вычисление площади криволинейной трапеции

Цель занятия: Научиться находить первообразные функций, вычислять площади фигур с помощью определенного интеграла.

Подготовка к занятию: Повторить теоретический материал по теме «Первообразная и интеграл»

Литература:

1. Алимов ш.А., Колягин ю.М. И др. «Алгебра и начала анализа 10-11»

2. Колмогоров а.М. И др. «Алгебра и начала математического анализа 10-11»

Задание на занятие:

1. Найти общий вид первообразной для функций:

1. 

2. 

3. 

4. 

2. Найти для функции f первообразную, график которой проходит через точку М:

1. , М(2; 15)

2. ,

3. Вычислить площади фигур, ограниченных линиями:

1. у = 2х – х², у = 0;

2. у = sin x, y = 0, x = 0, x = ;

3. y = x², y = 2x + 3.

4. Найти площадь каждой из фигур, на которые прямая у = х + 4 делит фигуру, ограниченную линиями 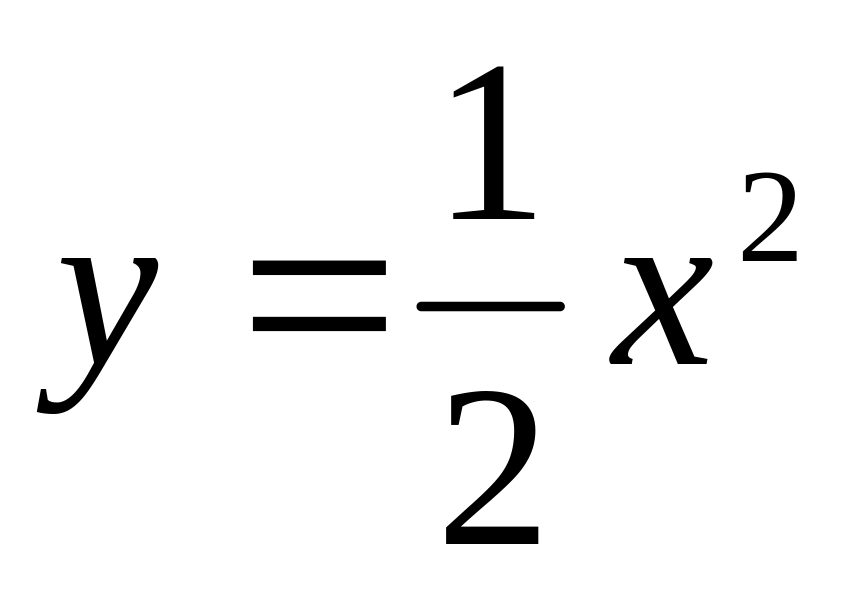и у = 8.

Порядок проведения занятия:

1. Получить допуск к работе;

2. Выполнить задания;

3. Ответить на контрольные вопросы.

Содержание отчета:

1. Наименование, цель занятия, задание;

2. Выполненное задание;

3. Ответы на контрольные вопросы.

Контрольные вопросы для зачета:

1. Запишите первообразные основных элементарных функций

2. По какой формуле вычисляется определенный интеграл?

3. Как с помощью определенного интеграла вычислить площадь фигуры?

Практическое занятие №31

Наименование занятия: Нахождение объемов тел

Цель занятия: Научиться вычислять объемы тел

Подготовка к занятию: Повторить теоретический материал по теме «Измерения в геометрии»

Литература:

1. Атанасян Л.С., Бутузов В.Ф., Кадомцев С.Б. и др. «Геометрия 10-11»

Задание на занятие:

1. Найти объем прямоугольного параллелепипеда ABCDA₁B₁C₁D₁, если АС = 15 см, DC₁ = см, DB₁ = 17 см.

2. Найти объем прямоугольного параллелепипеда, если известно, что его диагональ равна см и составляет с плоскостью основания угол в , а с плоскостью боковой грани – угол в .

3. Основанием прямой призмы служит прямоугольный треугольник с углом в . Расстояние от бокового ребра, проходящего через вершину прямого угла, до противолежащей боковой грани равно боковому ребру и равно 6 см. Найти объем призмы.

4. Основанием пирамиды РАВС служит прямоугольный треугольник АВС, , ВС = 6 см, 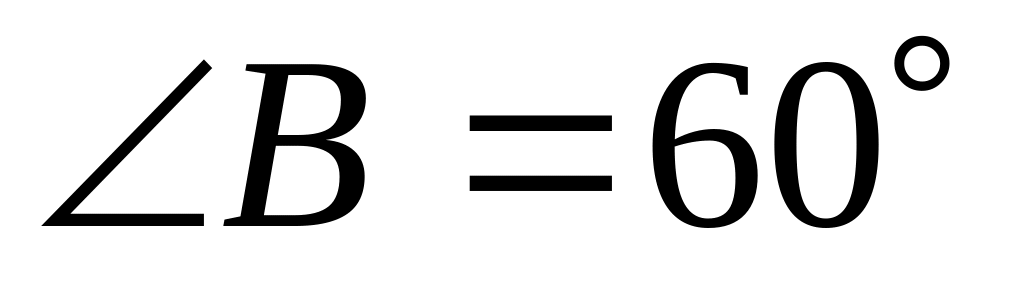. Грань АРС перпендикулярна плоскости основания, а две другие наклонены к нему под углом в . Найти объем пирамиды.

5. В цилиндр, площадь осевого сечения которого равна 24 см², вписана призма. Основанием призмы является прямоугольный треугольник с катетом, равным см, и прилежащим к нему углом в . Найти объем цилиндра.

6. Через вершину конуса проведена плоскость, пересекающая окружность основания по хорде, равной см и стягивающей дугу в . Плоскость составляет с плоскостью основания угол в . Найти объем конуса.

7. Площадь поверхности полушара равна 48π. Найти его объем.

Порядок проведения занятия:

1. Получить допуск к работе;

2. Выполнить задания;

3. Ответить на контрольные вопросы.

Содержание отчета:

1. Наименование, цель занятия, задание;

2. Выполненное задание;

3. Ответы на контрольные вопросы.

Контрольные вопросы для зачета:

1. Запишите формулы вычисления объемов параллелепипеда, призмы, пирамиды, цилиндра, конуса, шара.