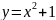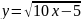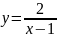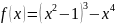Приложение к практическому занятию № 19.
Область
определения функции – множество значений
аргумента, при котором функция имеет
смысл. Область определения обозначается
символом
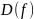 или
или
 .
.
Примеры:
Укажите для функций заданных формулами:
Квадратичная
функция.



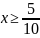
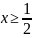
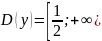
Так
как функция представляет собой дробь,
 или
или
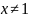
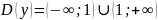
 .
Область определения функции должна
удовлетворять двум условиям:
.
Область определения функции должна
удовлетворять двум условиям:
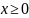
Или
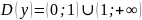
Найти наименьшее целое значение
 из области определения функции
из области определения функции

Найдём
область определения функции:
 и
и

 и
и


Наименьшее целое значение : 1.
Множество значений функции – множество чисел, состоящее из всех значений функции.
Обозначается
 .
.
Найти множество значений следующих функций:



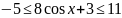
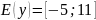
Приложение к практическому занятию № 20.
Функция
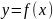 называется чётной, если для всех
называется чётной, если для всех
 выполняется равенство
выполняется равенство
 .
.
Функция
называется нечётной, если для всех
выполняется равенство
 .
.
Пример: Исследовать функцию на чётность и нечётность функции:
 ;
следовательно функция
;
следовательно функция
- чётная.
 следовательно
функция
- нечётная.
следовательно
функция
- нечётная.
Нули функции – точки, в которых функция обращается в нуль.
Пример: Найти нули функции:

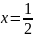 -
нуль функции
-
нуль функции

Нули фукнции:
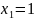
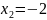
Промежутки знакопостоянства – интервалы, на которых функция положительна или отрицательна.
Пример: Найти промежутки знакопостоянства:

 при
при
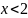
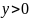 при
при
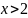
Наибольшее и наименьшее значение функции – самое большое или самое маленькое значение функции по сравнению со всеми возможными.
Найти наибольшее и наименьшее значение функции:
 .
Построим график этой функции в
прямоугольной системе координат.
Графиком является прямая. Для построения
берём два произвольных значения
аргумента и составляем таблицу значений
функции. Функция не имеет ни наибольшего
ни наименьшего значения.
.
Построим график этой функции в
прямоугольной системе координат.
Графиком является прямая. Для построения
берём два произвольных значения
аргумента и составляем таблицу значений
функции. Функция не имеет ни наибольшего
ни наименьшего значения.
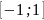 .
Строим график функции на отрезке
.
.
Строим график функции на отрезке
.
Наибольшее
и наименьшее значение функция принимает
на концах отрезка
.
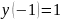 – наибольшее значение.
– наибольшее значение.
 - наименьшее значение.
- наименьшее значение.
Приложение к практическому занятию № 21.
Пусть
дана функция
.
Она имеет обратную, если из зависимости
можно переменную
однозначно выразить через переменную
 .
Для построения графика функции, обратной
для
.
Для построения графика функции, обратной
для
 , надо график исходной функции симметрично
отразить относительно прямой
, надо график исходной функции симметрично
отразить относительно прямой
 .
.
Примеры:
Найти функцию обратную для
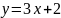 .
.
Областью определения и областью значений этой функции является все множество действительных чисел. Выразим x через y (другими словами, решим уравнение относительно x ).
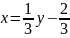
-
это и есть обратная функция, правда
здесь y –
аргумент, а x –
функция этого аргумента. Чтобы не
нарушать привычки в обозначениях (это
не имеет принципиального значения),
переставив буквы x и y ,
будем писать  .
.
Таким образом, и - взаимно обратные функции.
Приведем
графическую иллюстрацию взаимно обратных
линейных функций.

Найти функцию обратную для
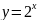 .
.
Областью
определения этой функции является все
множество действительных чисел, областью
значений является интервал  .
Выразим x через y (другими
словами, решим уравнение
относительно x).
.
Выразим x через y (другими
словами, решим уравнение
относительно x).
 -
это и есть обратная функция. Переставив
буквы x и y ,
имеем
-
это и есть обратная функция. Переставив
буквы x и y ,
имеем 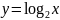 .
.
Таким образом, и - показательная и логарифмическая функции есть взаимно обратные функции на области определения.
График
взаимно обратных показательной и
логарифмической функций.