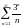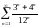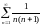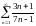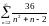- •§1 Числовые ряды. Основные понятия.
- •Задачи для самостоятельного решения
- •§2. Достаточные признаки сходимости знакоположительных рядов.
- •Задачи для самостоятельного решения
- •§3 Абсолютная и условная сходимость.
- •Задачи для самостоятельного решения
- •§4 Функциональные ряды.
- •Задачи для самостоятельного решения
- •§5 Ряды Фурье.
- •Задачи для самостоятельного решения
- •Список литературы
Оглавление
§1 Числовые ряды. Основные понятия. 2
Задачи для самостоятельного решения 3
§2. Достаточные признаки сходимости знакоположительных рядов. 3
Задачи для самостоятельного решения 4
§3 Абсолютная и условная сходимость. 6
Задачи для самостоятельного решения 7
§4 Функциональные ряды. 7
Задачи для самостоятельного решения 10
§5 Ряды Фурье. 11
Задачи для самостоятельного решения 13
Список литературы 15
§1 Числовые ряды. Основные понятия.
Пример 1.
Используя определение, исследовать ряд
на сходимость
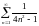 .
.
Решение:
Составим частичные суммы ряда:
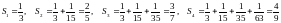 .
.
Таким образом,
получим последовательность частичных
сумм:
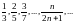 .
.
Т.е.
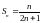 .
.
Найдем предел:
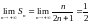 .
По определению ряд сходится и его сумма
равна 0,5.
.
По определению ряд сходится и его сумма
равна 0,5.
Пример 2.
Показать, что ряд сходится и найти его
сумму
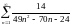 .
.
Решение:
Разложим общий член ряда в сумму простейших дробей
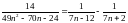 .
.
Запишем n-ую частичную сумму
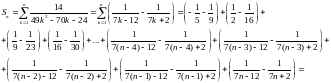
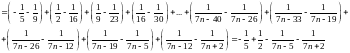
Мы заметили, что (k-2)-й и k-й члены содержат одно и то же выражение с противоположными знаками.
Найдем предел
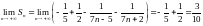 .
.
То есть данный ряд сходится и его сумма равна 0,3.
Пример 3.
Исследовать ряд на сходимость
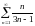 .
.
Решение:
Пользуясь необходимым признаком сходимости, докажем расходимость ряда.
Найдем
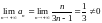 .
Ряд расходится.
.
Ряд расходится.
Задачи для самостоятельного решения
Исследовать ряды на сходимость:
Ответы:
1) s=13/2; 2) расходится; 3) s=7/2; 4) s=2; 5) расходится; 6) s=5/6; 7) s=1; 8) расходится; 9) s=22.
§2. Достаточные признаки сходимости знакоположительных рядов.
Пример 1.
Исследовать ряд на сходимость
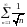 .
.
Решение:
Используем
признак сравнения. Сравним члены данного
ряда с членами гармонического ряда
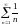 ,
который расходится:
,
который расходится:
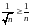 .
Так как ряд с меньшими членами расходится,
то и данный ряд с большими членами
.
Так как ряд с меньшими членами расходится,
то и данный ряд с большими членами
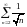 так же расходится.
так же расходится.
Пример 2. Исследовать ряд на сходимость
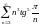 .
.
Решение:
Используем
предельный признак сравнения. Возьмем
обобщенный гармонический ряд
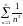 .
Он сходится, т.к. степень знаменателя
больше 1. Вычислим предел отношения
общих членов этих рядов
.
Он сходится, т.к. степень знаменателя
больше 1. Вычислим предел отношения
общих членов этих рядов
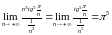 .
.
Получили конечный, не равный нулю, предел. Значит, ряды ведут себя одинаково. Исходный ряд также сходится.
Пример 3. Исследовать ряд на сходимость
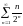 .
.
Решение:
Используем признак Даламбера.
Вычислим предел отношения последующего члена к предыдущему:
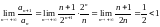 .
Ряд сходится.
.
Ряд сходится.
Пример 4.
Исследовать ряд на сходимость
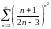 .
.
Решение:
Используем радикальный признак Коши.
Вычислим предел корня n-ой степени из общего члена:
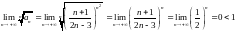 .
Ряд сходится.
.
Ряд сходится.
Пример 5. Исследовать ряд на сходимость
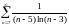 .
.
Решение:
Заметим, что
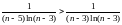 .
.
Будем
исследовать на сходимость ряд
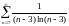
Используем интегральный признак Коши.
Так как
функция
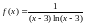 удовлетворяет условиям признака, а
именно монотонна, положительна и
удовлетворяет условиям признака, а
именно монотонна, положительна и
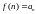 при
при
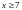 ,
то исследование сходимости ряда сводится
к исследованию сходимости интеграла
,
то исследование сходимости ряда сводится
к исследованию сходимости интеграла
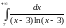 .
.
Интеграл
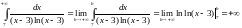 расходится. Следовательно, расходится
и ряд
.
расходится. Следовательно, расходится
и ряд
.
По признаку сравнения, раз расходится ряд с меньшими членами, то расходится и ряд с большими членами. Значит, исходный ряд расходится.
Задачи для самостоятельного решения
Исследовать ряды на сходимость:
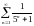
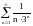
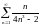
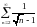
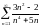
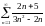
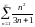
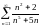
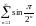
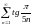
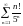
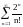
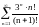
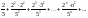
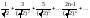
а)
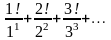 ;
б)
;
б)
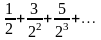 .
.
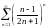
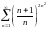
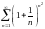
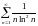
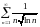
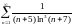
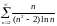

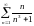
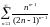
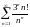
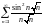
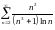

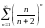
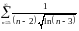
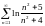
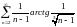
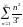
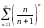
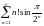
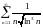
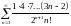

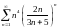
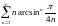
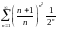
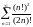
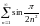

Ответы:
1) сходится; 2) сходится; 3) сходится; 4) расходится; 5) сходится; 6) расходится; 7) расходится; 8) сходится; 9) сходится; 10) расходится; 11) расходится; 12) сходится; 13) расходится; 14) сходится; 15) сходится; 16) а) сходится, б) сходится; 17) сходится; 18) сходится; 19) расходится; 20) расходится; 21) сходится; 22) расходится; 23) сходится; 24) расходится; 25) сходится; 26) расходится; 27) сходится; 28) сходится; 29) расходится; 30) сходится; 31) расходится; 32) расходится; 33) расходится; 34) расходится; 35) сходится; 36) сходится; 37) сходится; 38) расходится; 39) расходится; 40) сходится; 41) расходится; 42) сходится; 43) сходится; 44) сходится; 45) расходится; 46) сходится; 47) сходится; 48) сходится.