
- •Математический анализ
- •Купцов Михаил Иванович, Баева Ольга Владимировна математический анализ
- •Методические указания по выполнению контрольной работы
- •Учебно-методический план
- •Задания контрольной работы
- •Примерные вопросы к экзамену
- •Литература Базовый учебник
- •Дополнительная литература
- •Содержание
Задания контрольной работы
№ 1-20. Вычислить указанные пределы:
а)
 ; б)
; б)
 ; в)
; в)
 ;
г)
;
г) 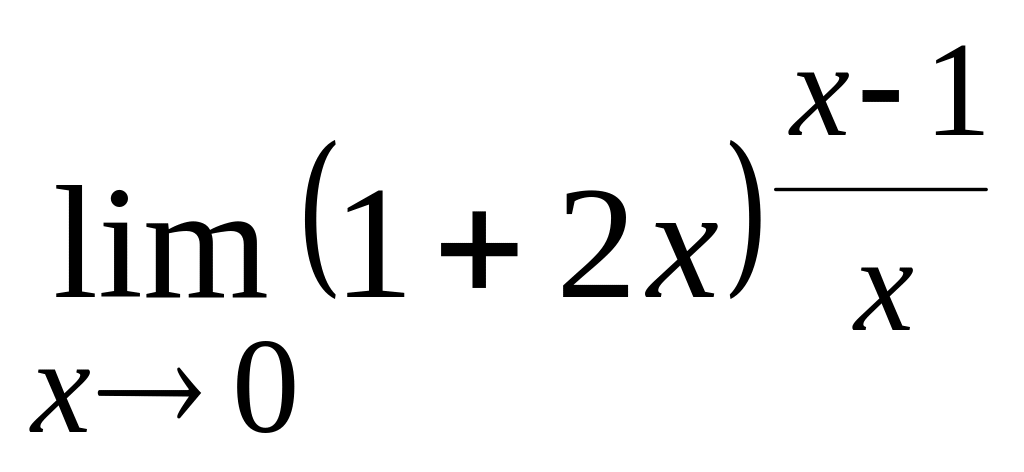 .
.
а)
 ;
б)
;
б) ;
в)
;
в) ;
г)
;
г)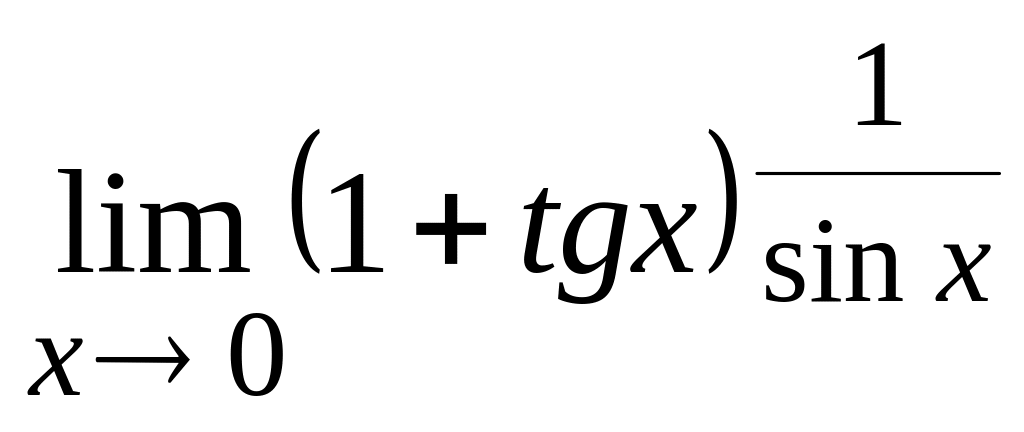 .
.
а) ; б) ; в)
 ;
г)
;
г)  .
.
а)
 ;
б)
;
б)
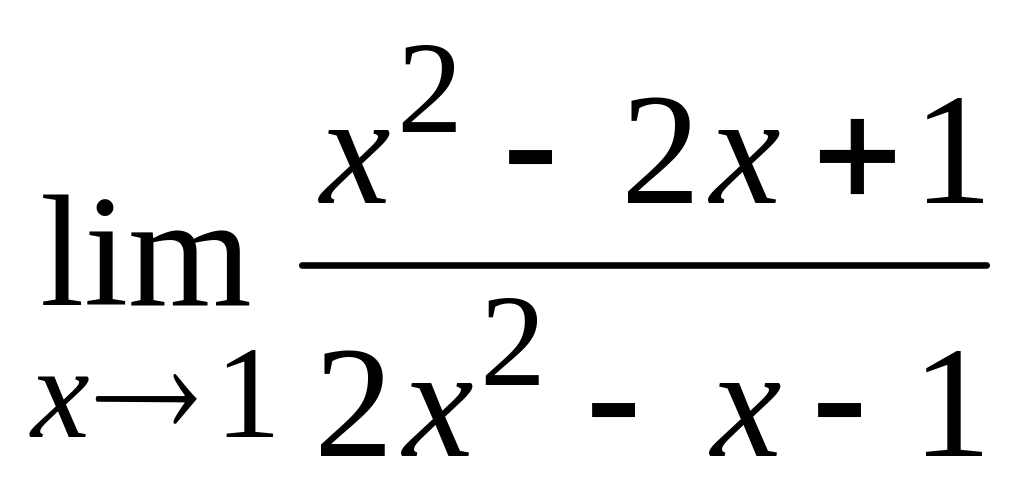 ;
в)
;
в)
 ; г)
; г) 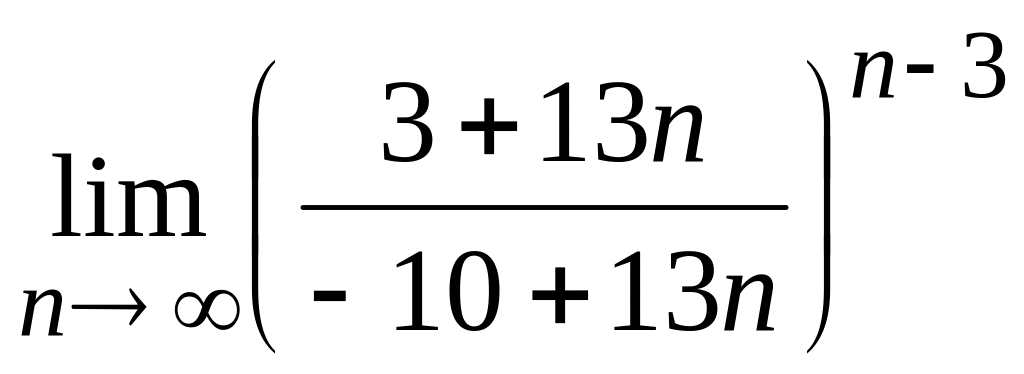 .
.
а)
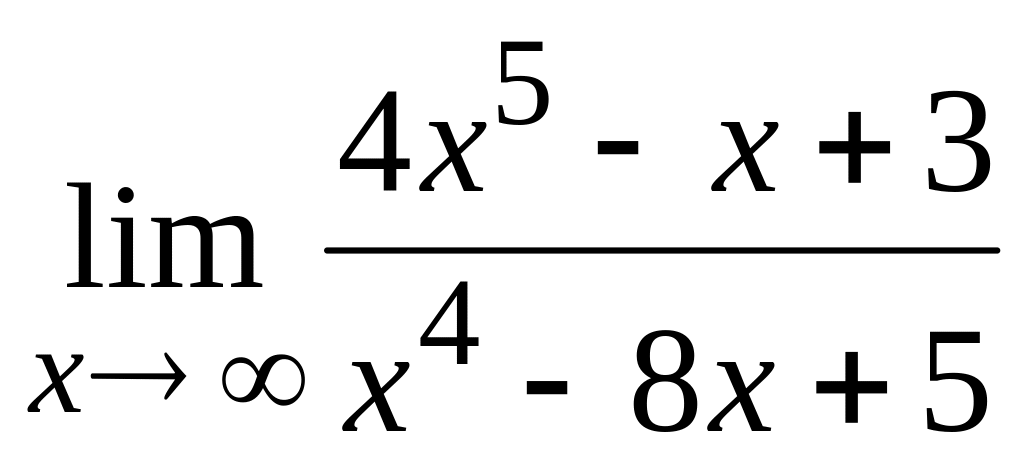 ;
б)
;
б) ;
в)
;
в)  ;
г)
;
г) .
.
а)
 ;
б)
;
б)
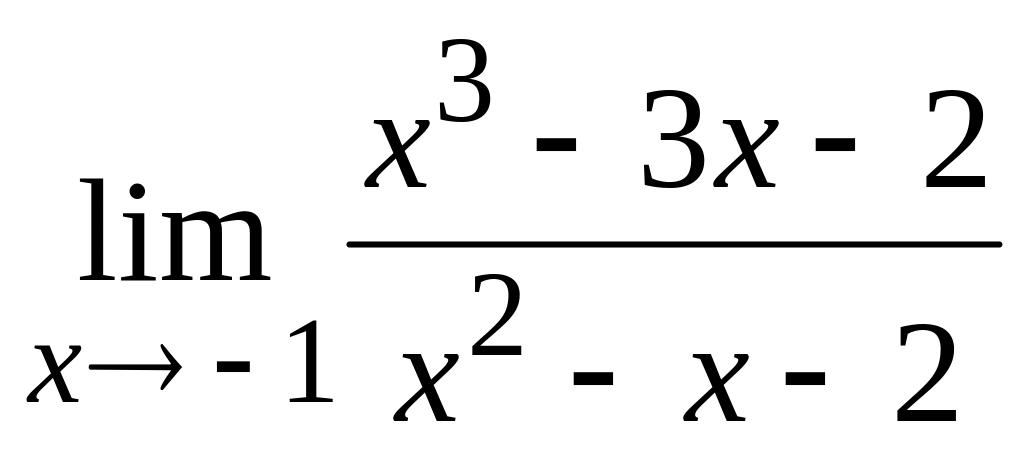 ;
в)
;
в)
 ;
г)
;
г) 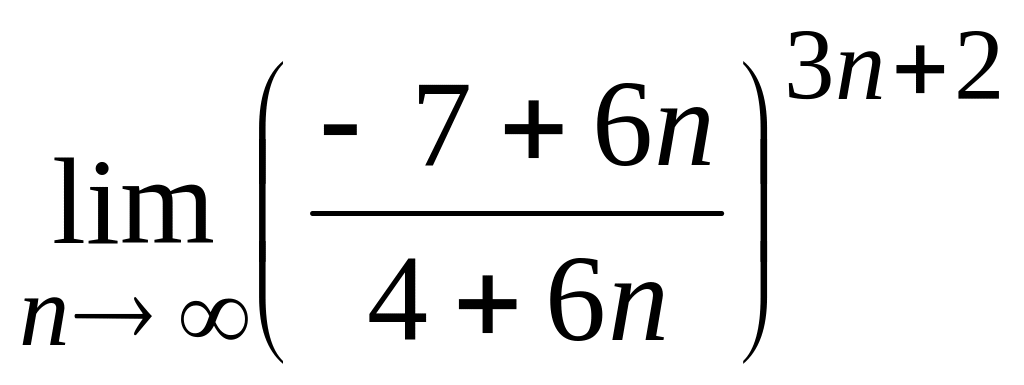 .
.
а)
 ;
б)
;
б)
 ;
в)
;
в)
 ;
г)
;
г)  .
.
а)
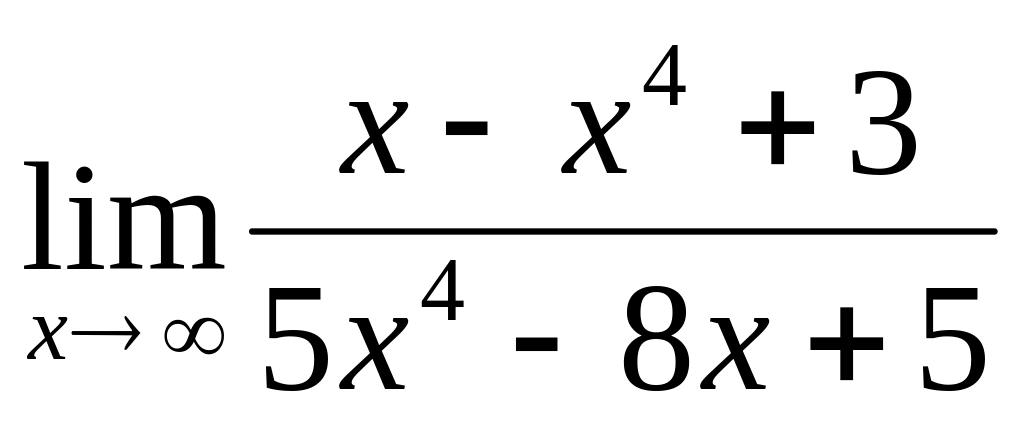 ;
б)
;
б)
 ;
в)
;
в)
 ;
г)
;
г)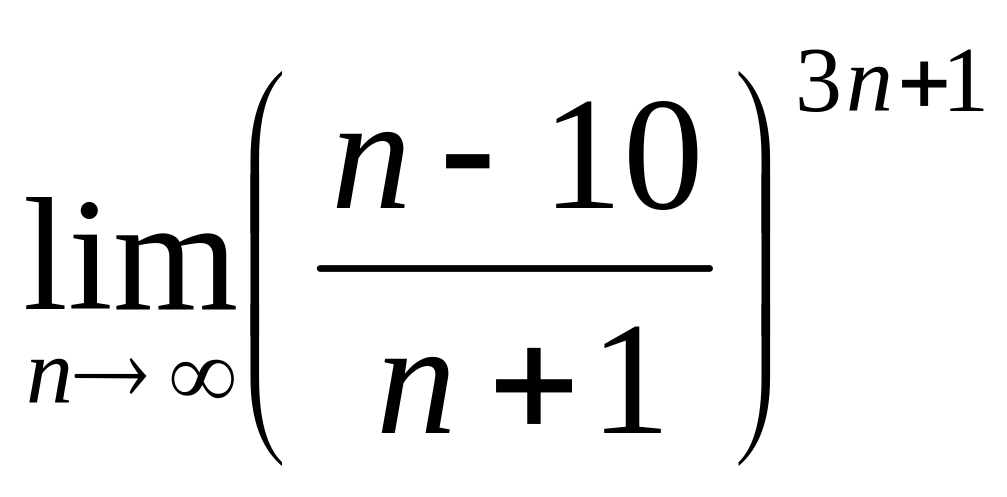 .
.
а)
 ;
б)
;
б) ;
в)
;
в) ;
г)
;
г)
 .
.а)
 ;
б)
;
б) ;
в)
;
в) ;
г)
;
г)  .
.
а)
 ;
б)
;
б) ;
в)
;
в) ;
г)
;
г)  .
.
а)
 ;
б)
;
б) ;
в)
;
в) ;
г)
;
г)  .
.
а)
 ;
б)
;
б) ;
в)
;
в) ;
г)
;
г)  .
.
а)
 ;
б)
;
б) ;
в)
;
в) ;
г)
;
г)  .
.
а)
 ;
б)
;
б) ; в)
; в) ;
г)
;
г)  .
.
а)
 ;
б)
;
б) ;
в)
;
в)  ;
г)
;
г) 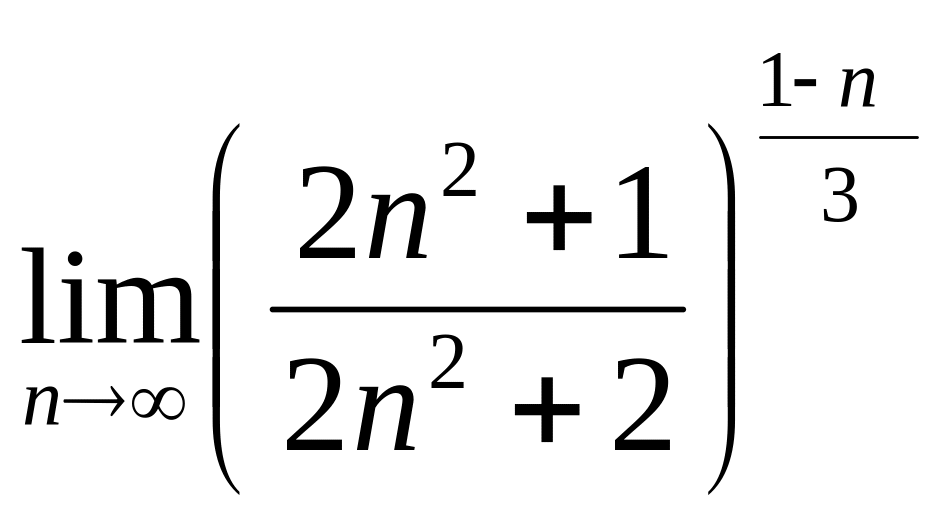 .
.
а)
 ;
б)
;
б) ;
в)
;
в) ;
г)
;
г) 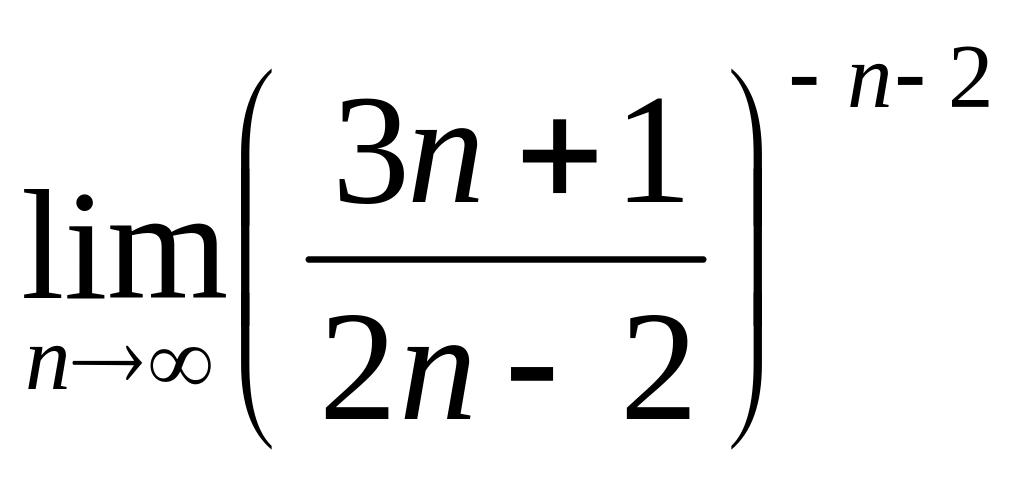 .
.
а)
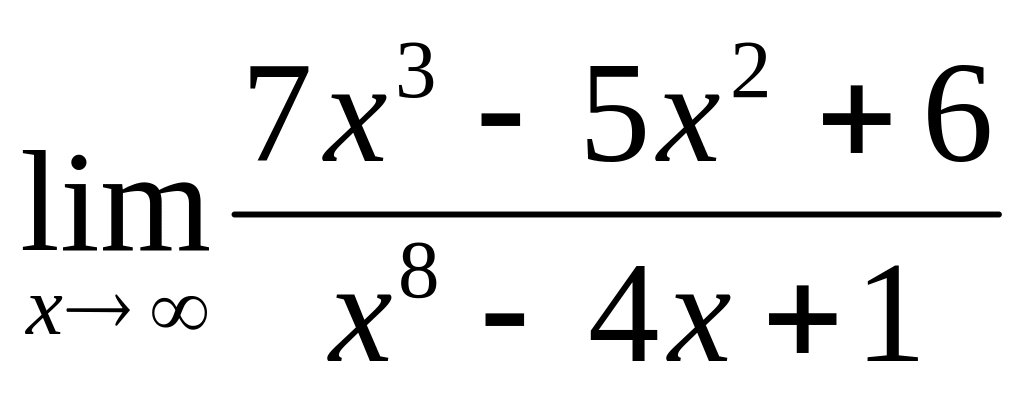 ;
б)
;
б)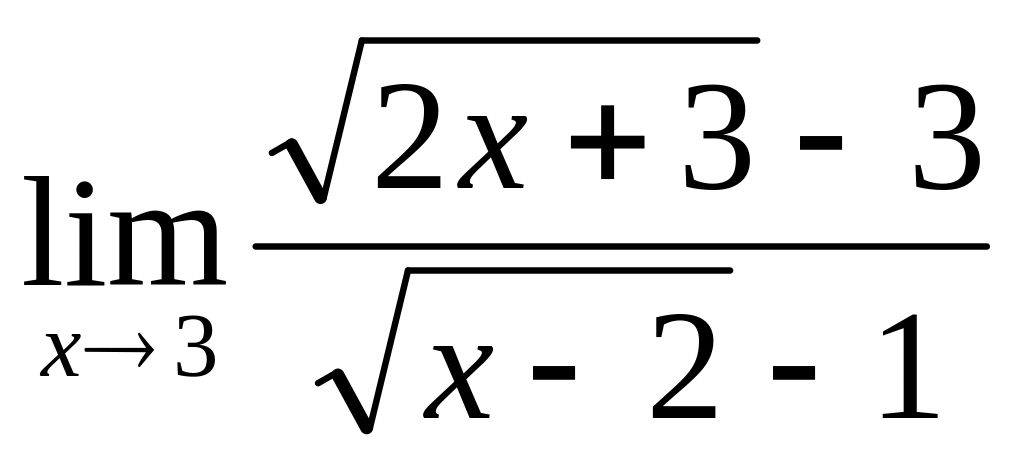 ;
в)
;
в) ;
г)
;
г)  .
.
а)
 ;
б)
;
б) ;
в)
;
в) ;
г)
;
г)  .
.
а)
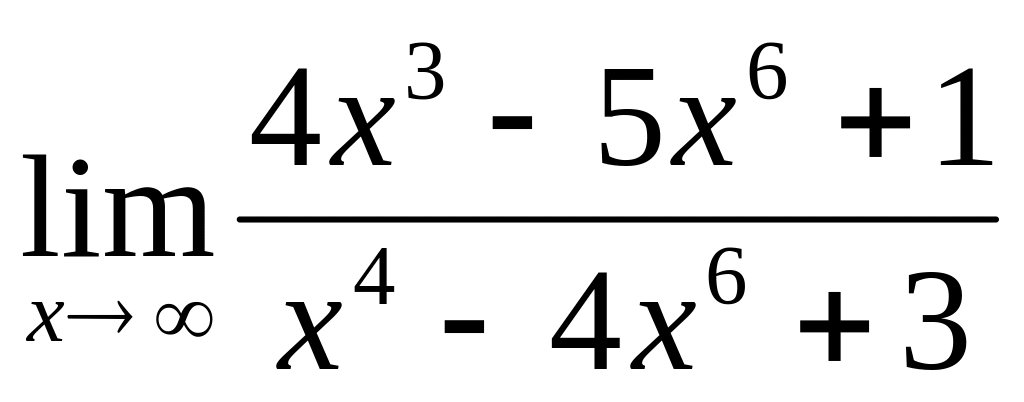 ;
б)
;
б) ;
в)
;
в) ;
г)
;
г)  .
.
№ 21-40.
Определить производные
![]() ,
пользуясь формулами дифференцирования.
,
пользуясь формулами дифференцирования.
а)
 б)
б)
 в)
в)
 г)
г) 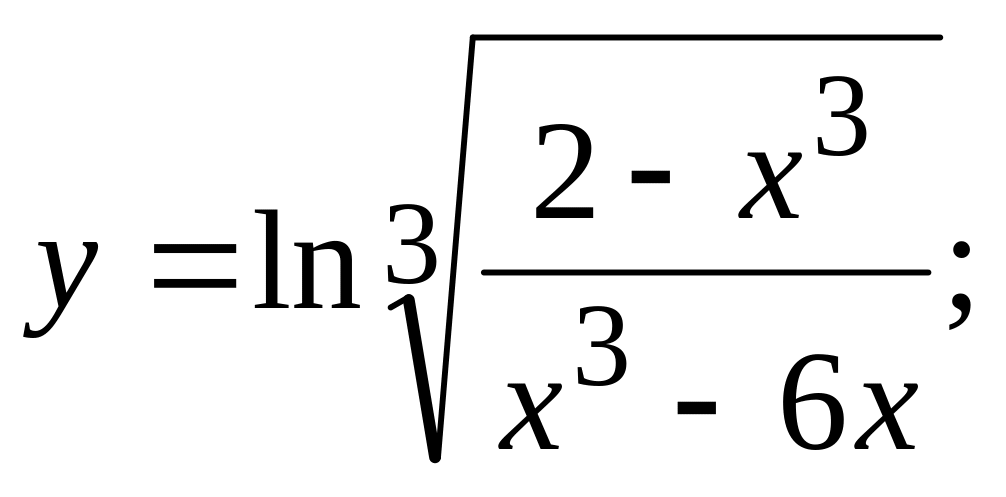 д)
д)

а)
 б)
б)
 в)
в)
 г)
г) 
д)
![]()
а)
 б)
б)
 в)
в)
 г)
г)  д)
д)

а)
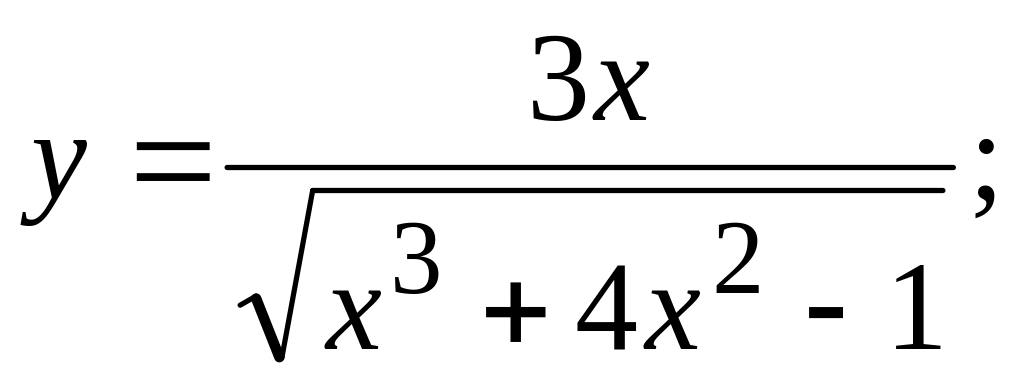 б)
б)
 в)
в)

г)
![]() д)
д)
![]()
а)
 б)
б)
 в)
в)
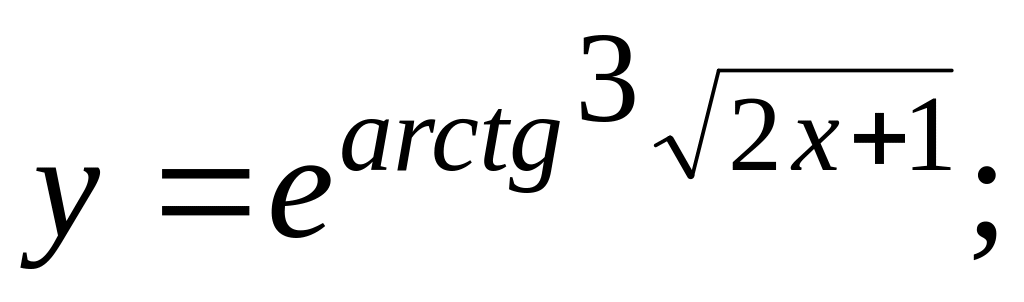 г)
г)  д)
д)

а)
 б)
б)
 в)
в)
 г)
г)  д)
д)

а)
 б)
б)
 в)
в)
 г)
г) 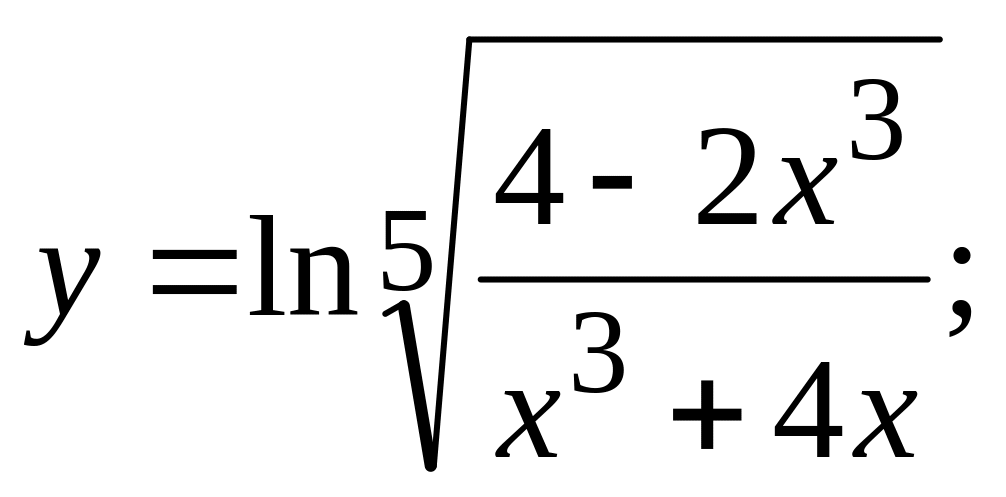 д)
д)

а)
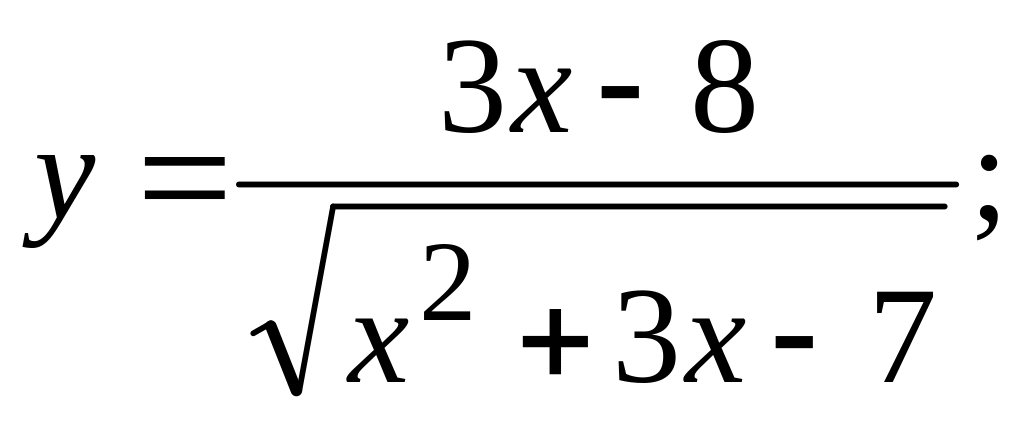 б)
б)
 в)
в)
 г)
г)  д)
д)

а)
 б)
б)
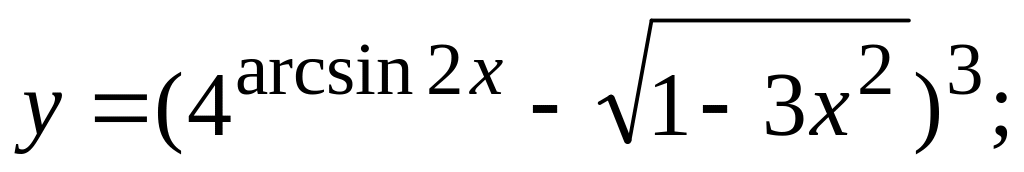 в)
в)
 г)
г)  д)
д)
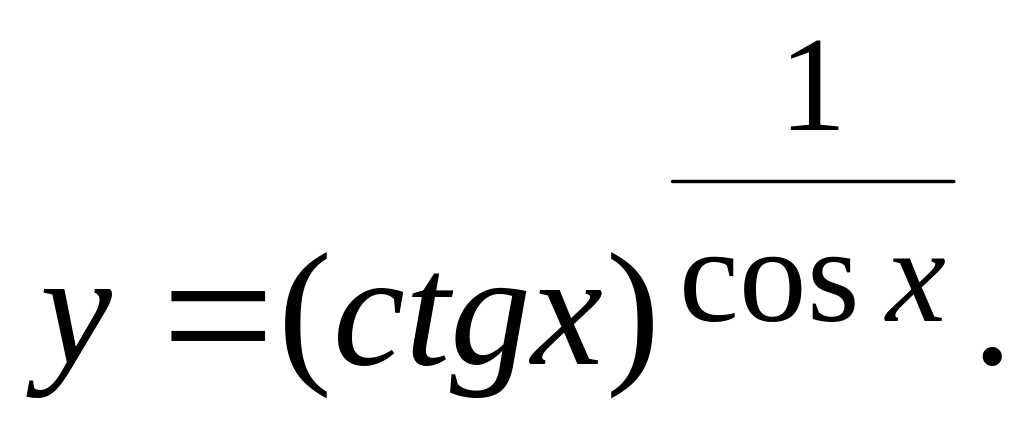
а)
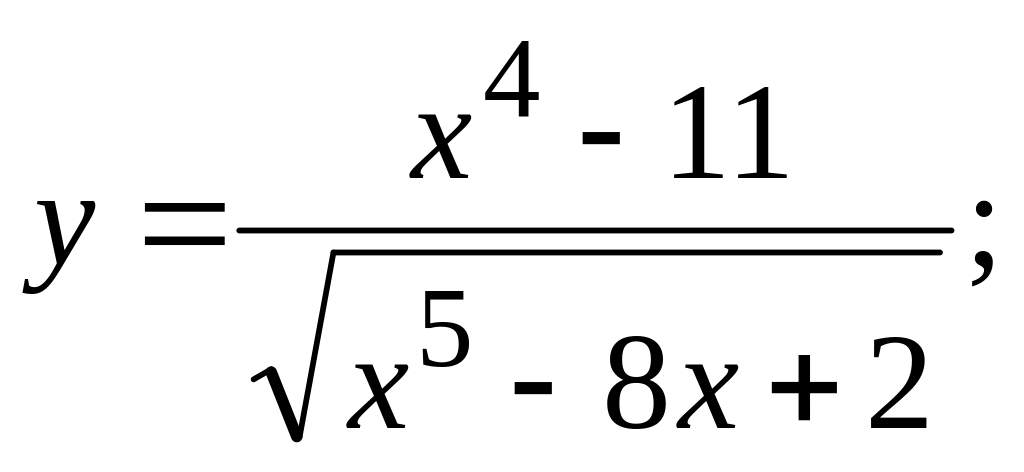 б)
б)
 в)
в)
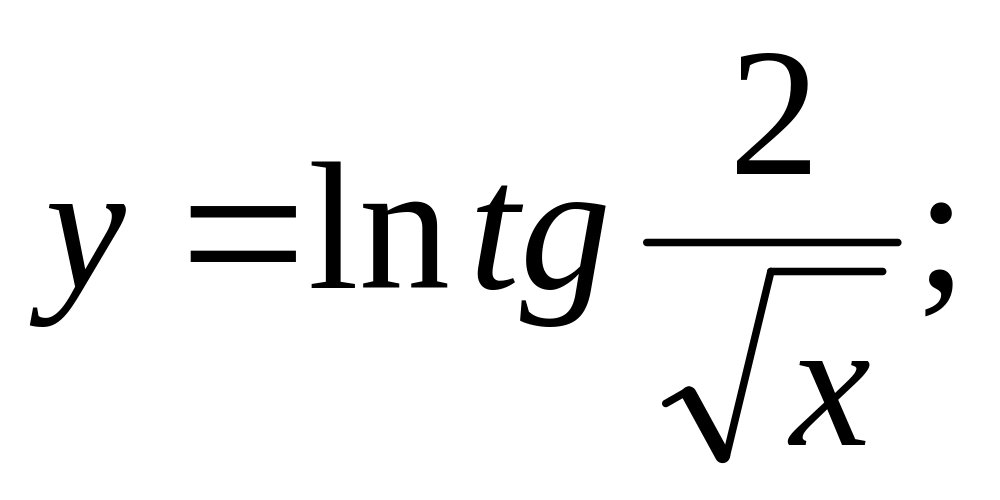 г)
г) 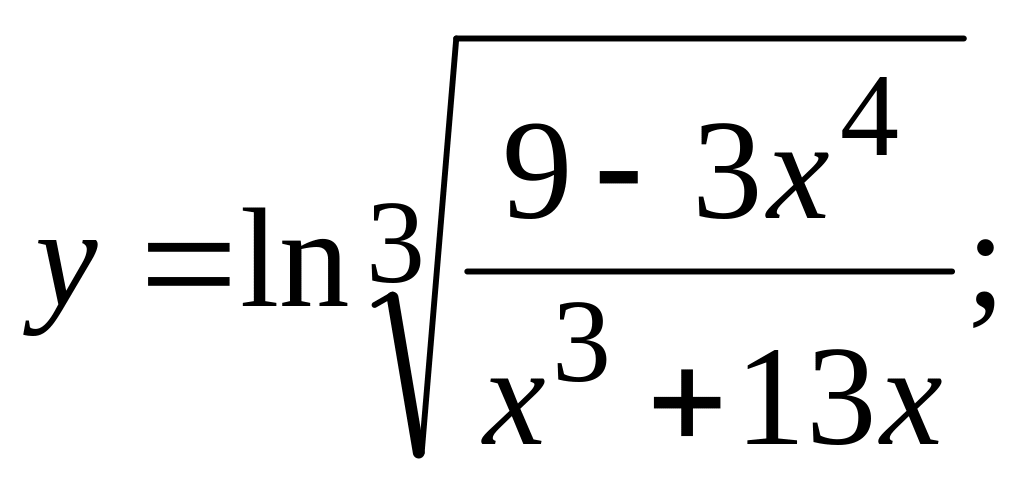 д)
д)
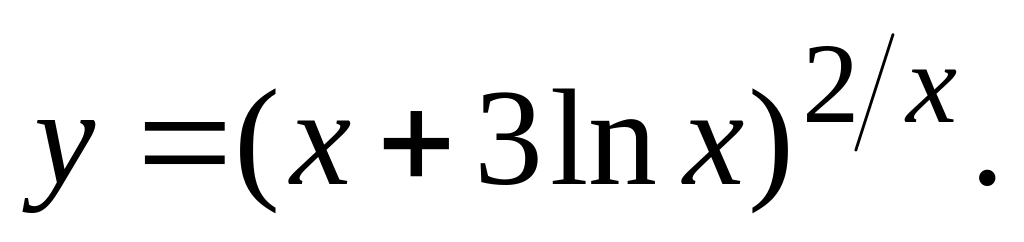
а)
 б)
б)
 в)
в)
 г)
г) 
д)
![]()
а)
 б)
б)
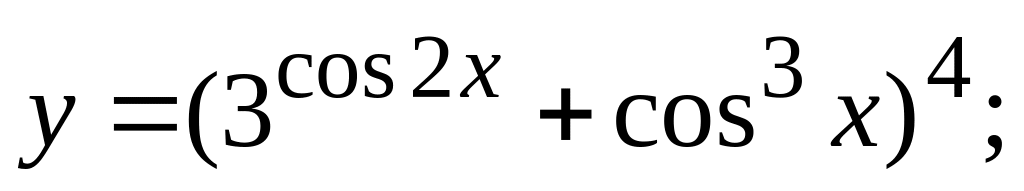 в)
в)
 г)
г) 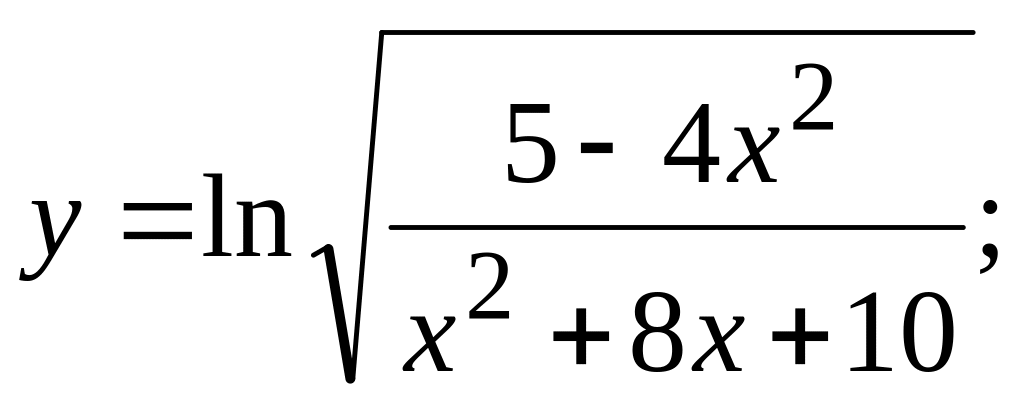 д)
д)

а)
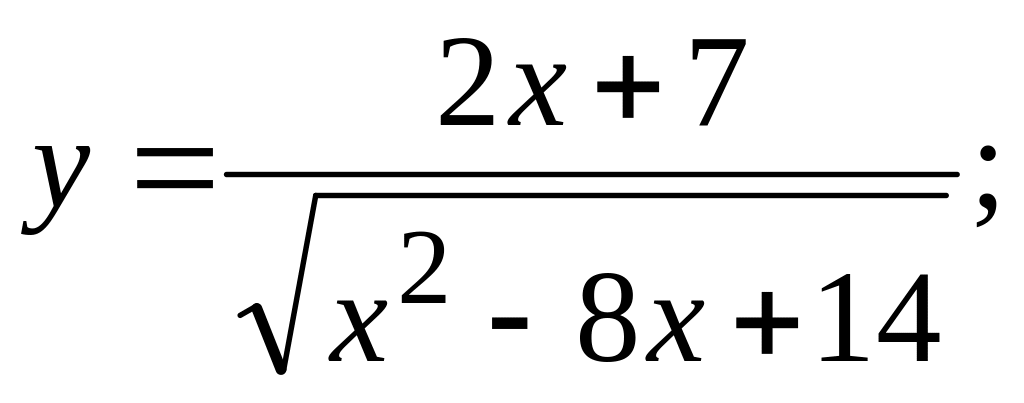 б)
б)
 в)
в)
 г)
г)  д)
д)

а)
 б)
б)
 в)
в)
 г)
г) 
д)
![]()
а)
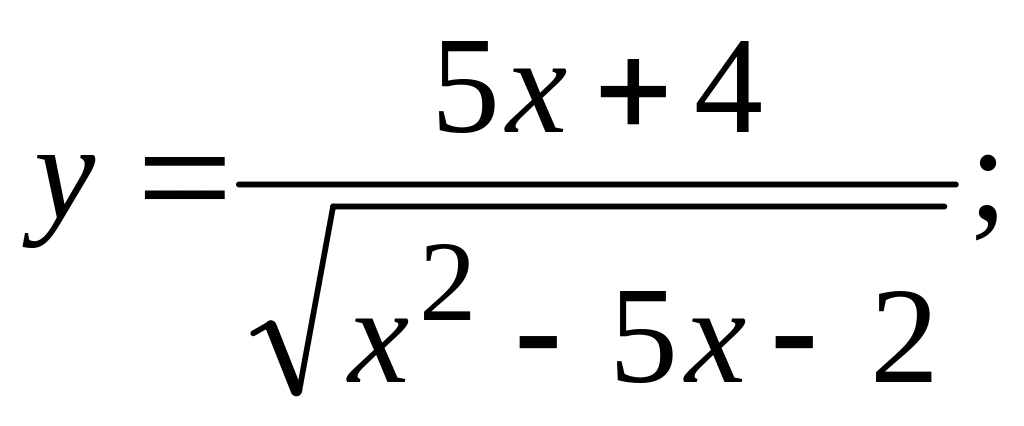 б)
б)
 в)
в)
 г)
г)  д)
д)

а)
 б)
б)
 в)
в)
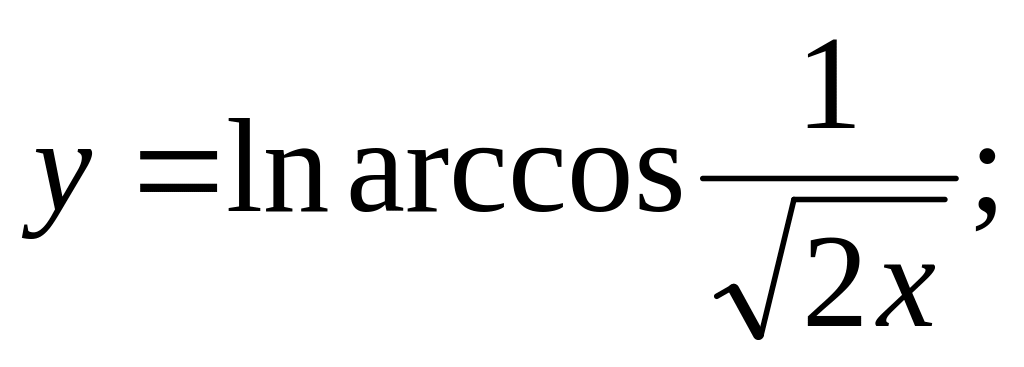 г)
г)  д)
д)
а)
 ; б)
; б)
 в)
в)
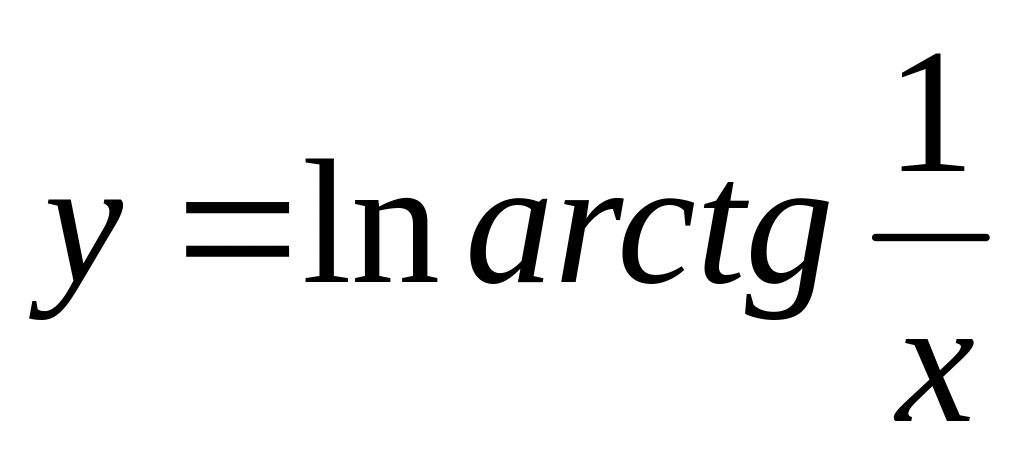 ;
;
г) ![]() д)
д)
![]()
а)
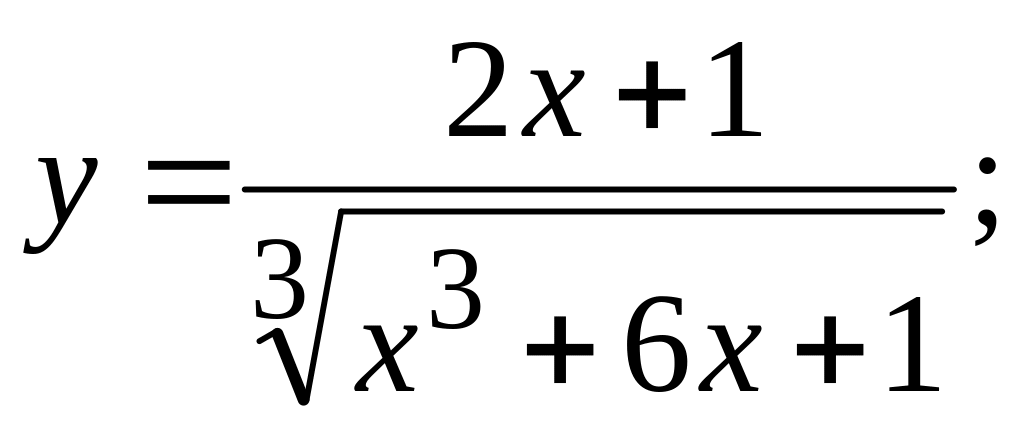 б)
б)
 в)
в)
 г)
г)  д)
д)

а)
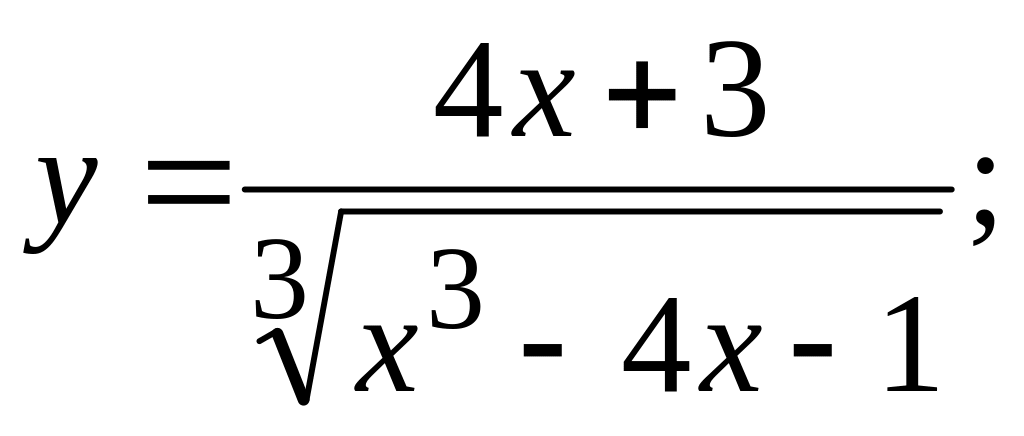 б)
б)
 в)
в)
 г)
г)  д)
д)
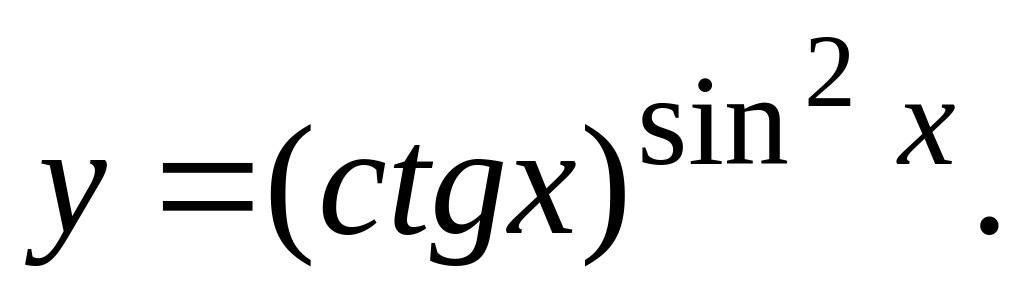
а)
 б)
б)
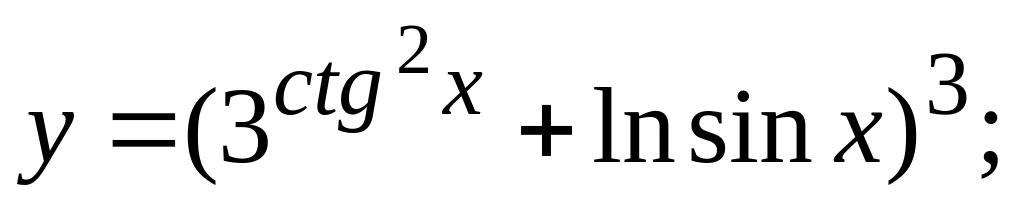 в)
в)
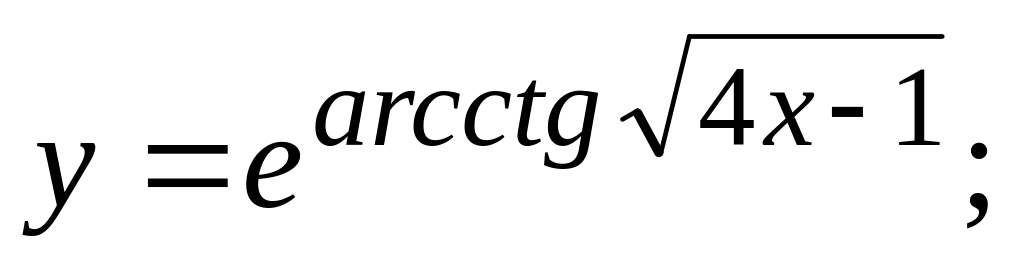 г)
г)  д)
д)

№ 41-60. Исследовать данные функции методами дифференциального исчисления и начертить их графики.
Исследование и построение графика рекомендуется проводить по следующей схеме:
1) найти область определения функции;
2) исследовать функцию на непрерывность; найти точки разрыва функции и ее односторонние пределы в точках разрыва;
3) выяснить, не является ли данная функция четной, нечетной;
4) найти точки экстремума функции и определить интервалы возрастания и убывания функции;
5) найти точки перегиба графика функции и определить интервалы выпуклости и вогнутости графика функции;
6) найти асимптоты графика функции, если они имеются;
7) построить график функции, используя результаты исследования; при необходимости можно дополнительно находить точки графика, давая аргументу х ряд значений и вычисляя соответствующие значения у.
№ 61-80. Вычислить интегралы:
а)
 ;
б)
;
б)
 ;
в)
;
в) .
.
а)
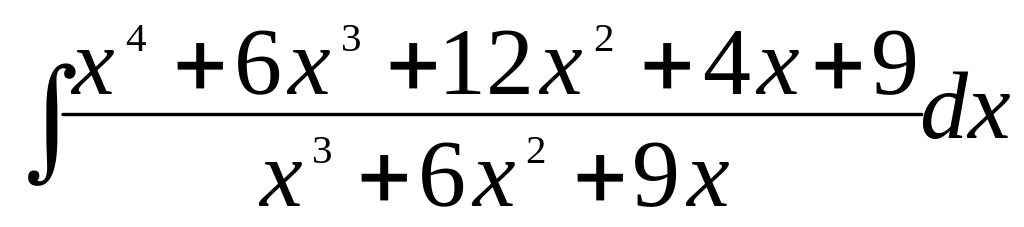 ;
б)
;
б)
 ;
в)
;
в)
 .
.
а)
 ;
б)
;
б)
 ;
в)
;
в)
 .
.
а)
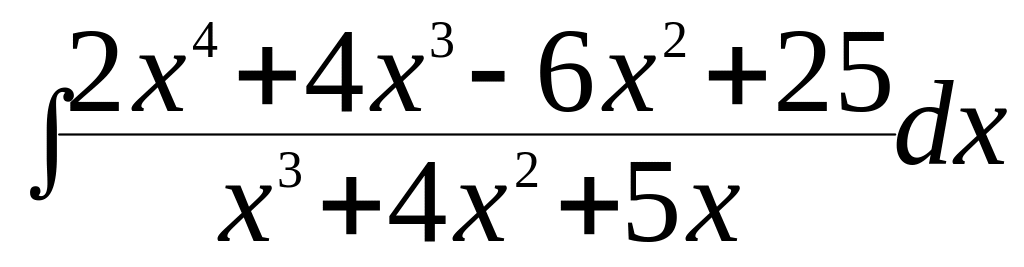 ;
б)
;
б) ;
в)
;
в)
 .
.
а)
 ;
б)
;
б)
 ;
в)
;
в)
 .
.
а)
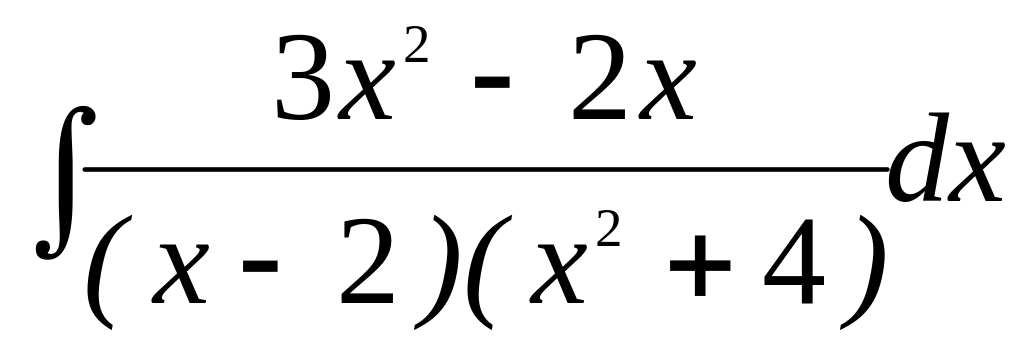 ;
б)
;
б)
 ;
в)
;
в)
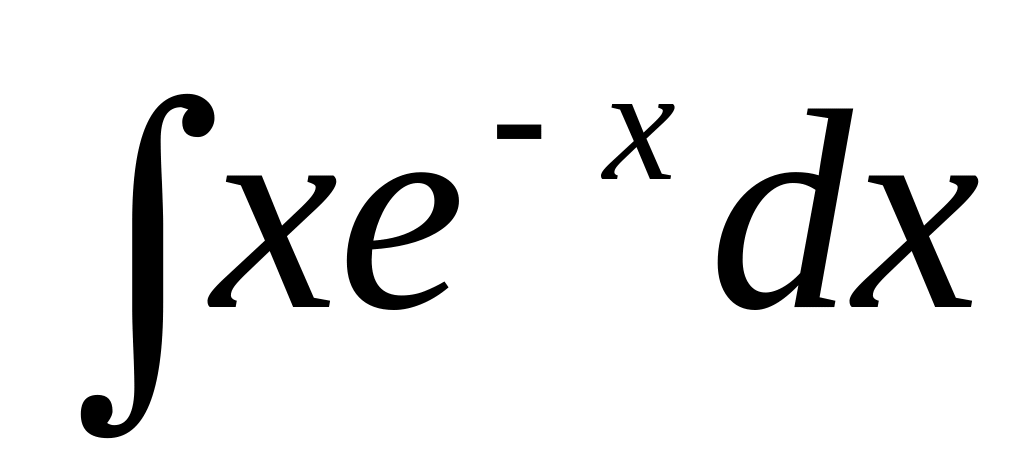 .
.
а)
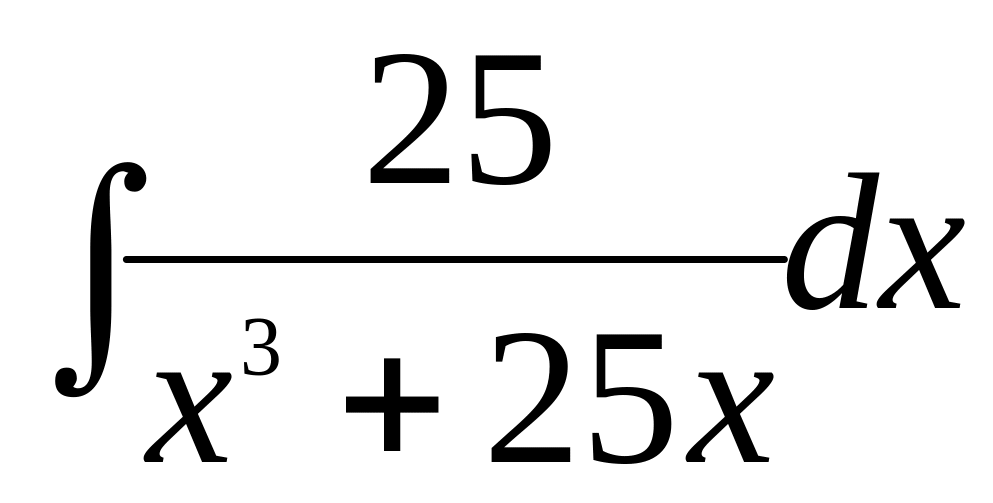 ;
б)
;
б)
 ;
в)
;
в)
 .
.
а)
 ;
б)
;
б)
 ;
в)
;
в)
 .
.
а)
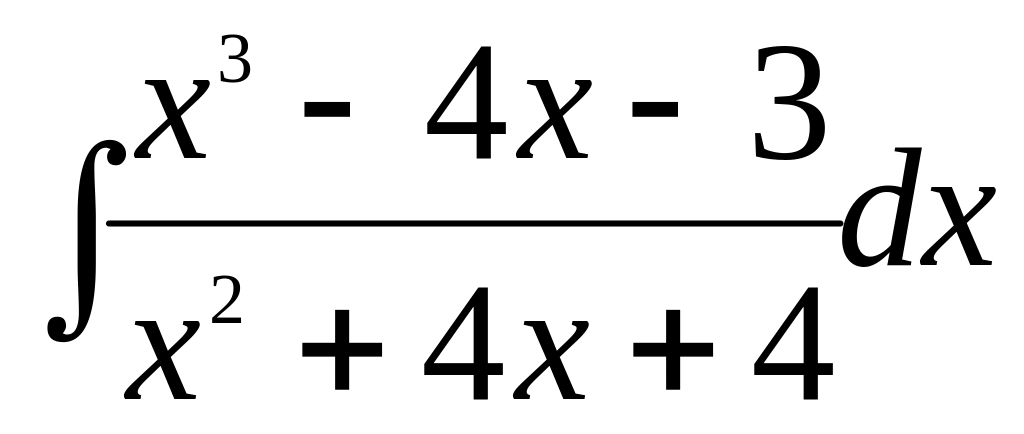 ;
б)
;
б)
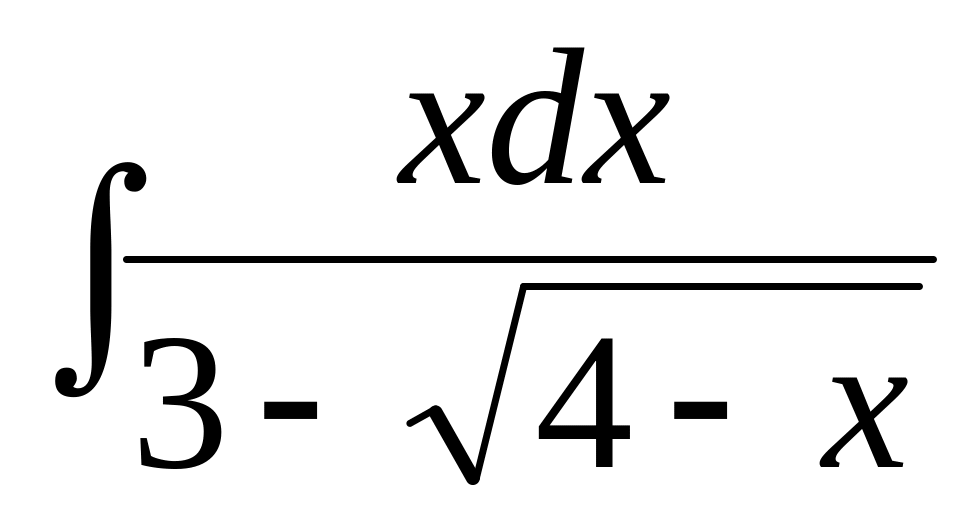 ;
в)
;
в)
 .
.
а)
 ;
б)
;
б)
 ;
в)
;
в)
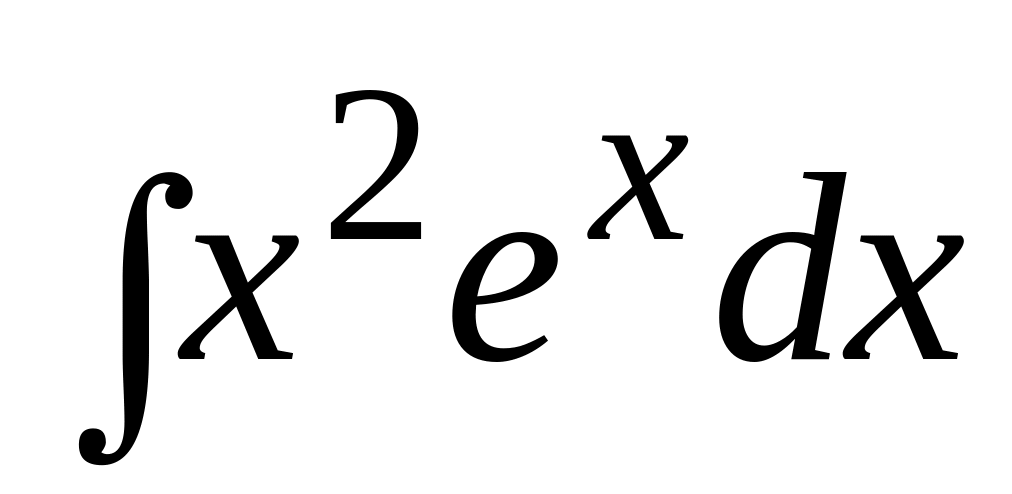 .
.
а)
 ;
б)
;
б) ;
в)
;
в)
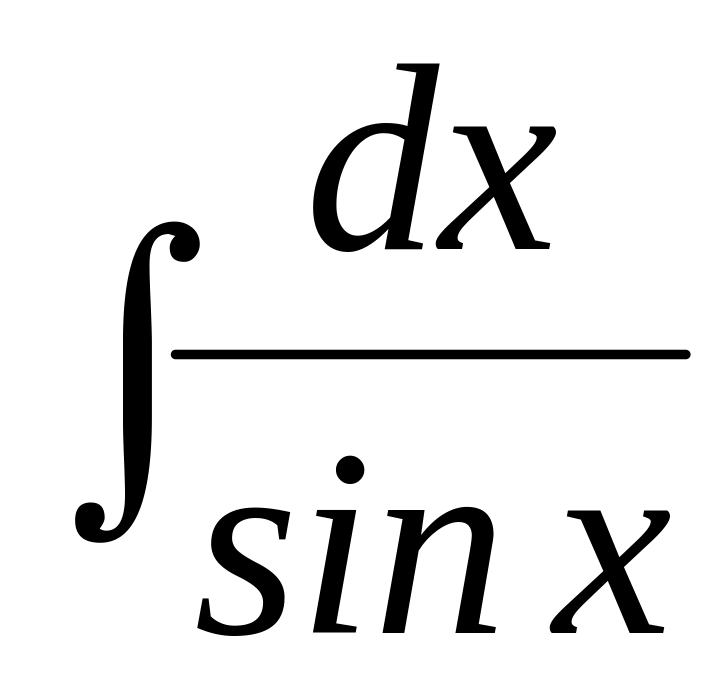 .
.
а)
 ;
б)
;
б)
 ;
в)
;
в)
 .
.
а)
 ;
б)
;
б)
 ;
в)
;
в)
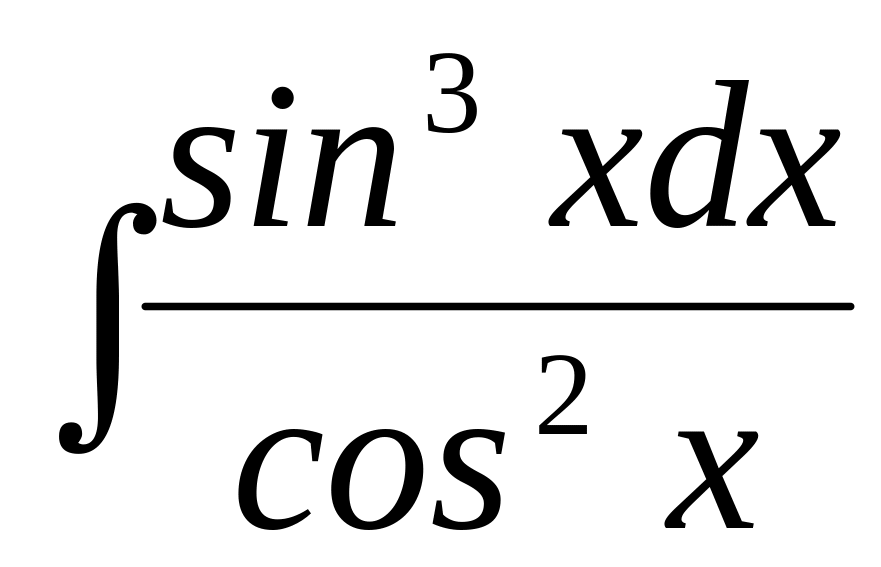 .
.
а)
 ;
б)
;
б) ;
в)
;
в)
 .
.
а)
 ;
б)
;
б)
 ;
в)
;
в)
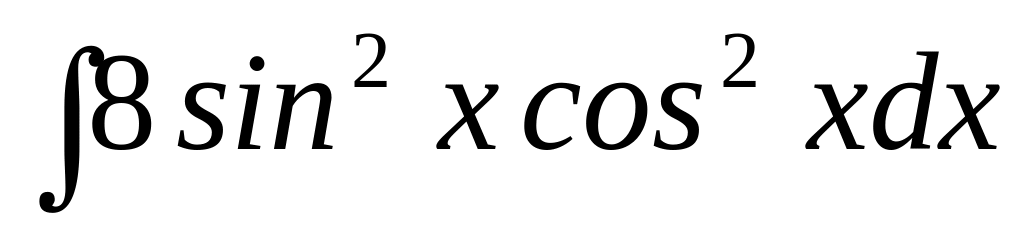 .
.
а)
 ;
б)
;
б)
 ;
в)
;
в)
 .
.
а)
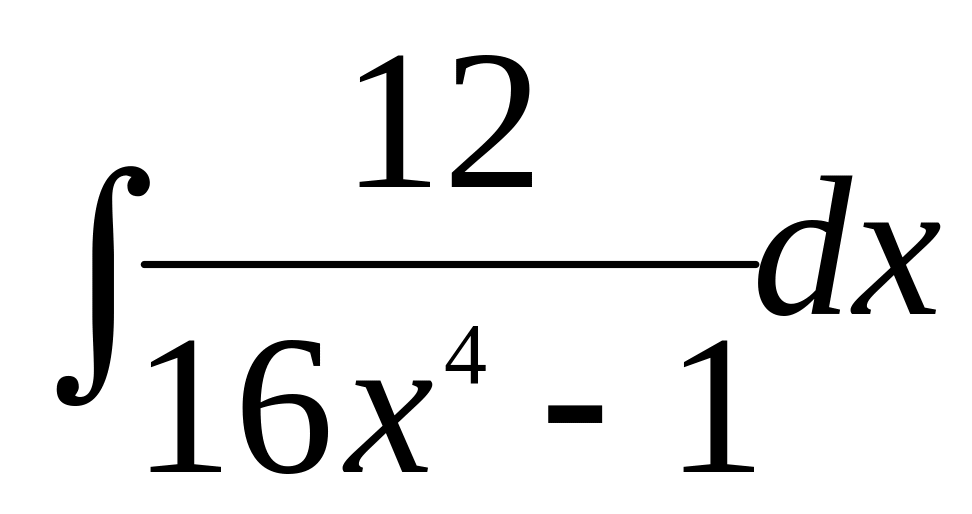 ;
б)
;
б) ;
в)
;
в)
 .
.
а)
 ;
б)
;
б) ;
в)
;
в)
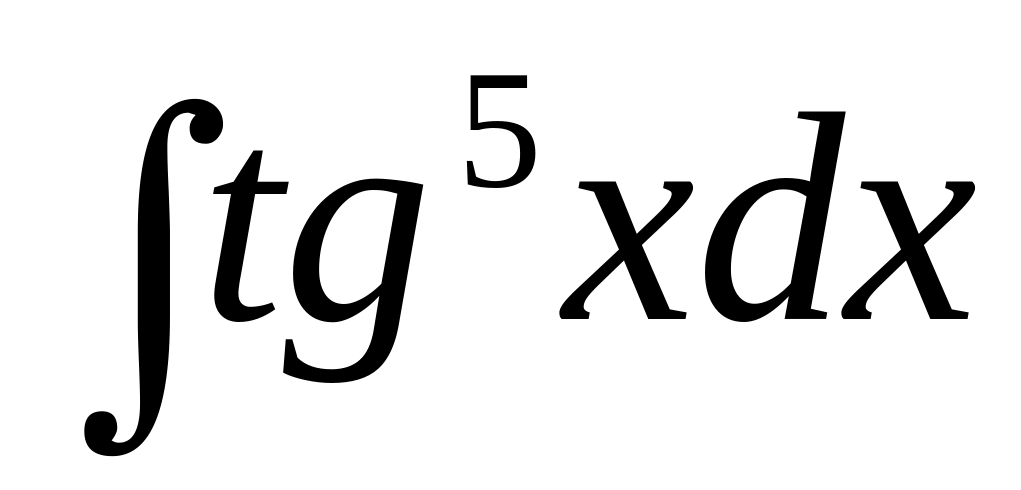 .
.
а)
 ;
б)
;
б)
 ;
в)
;
в)
 .
.
а)
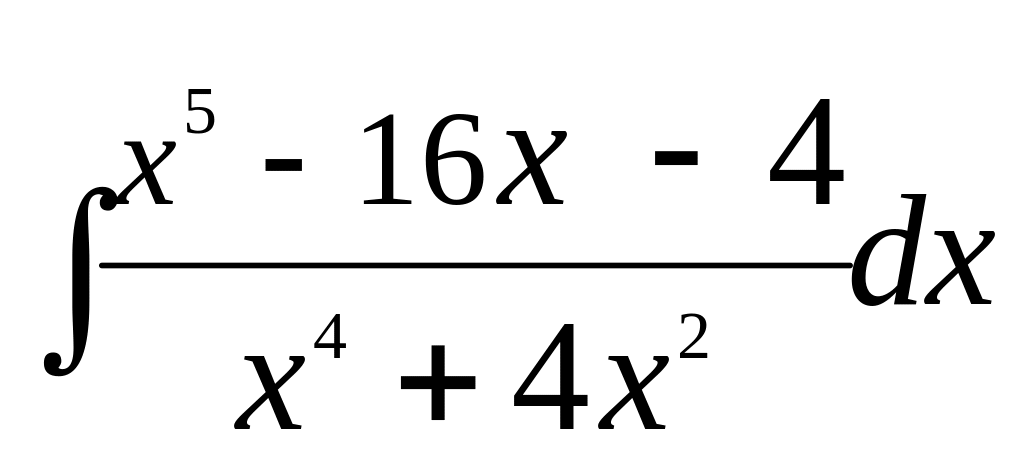 ;
б)
;
б)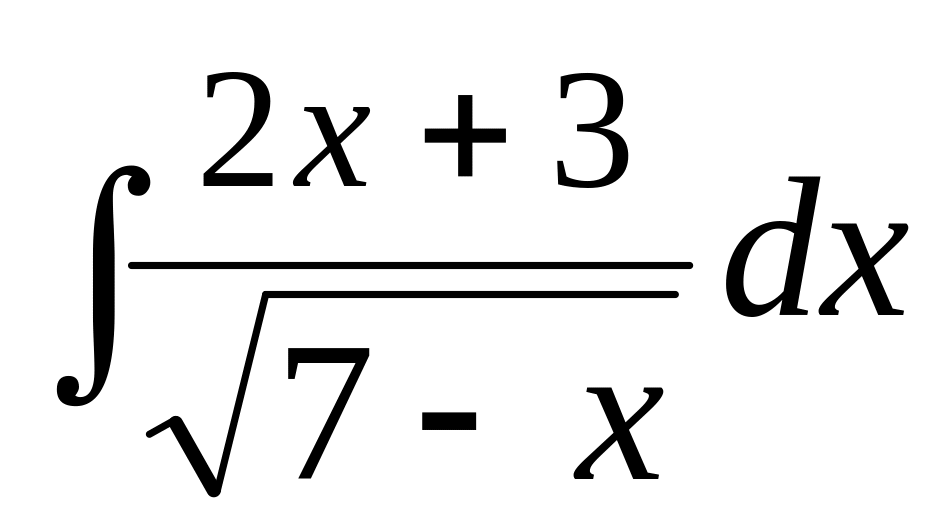 ;
в)
;
в)
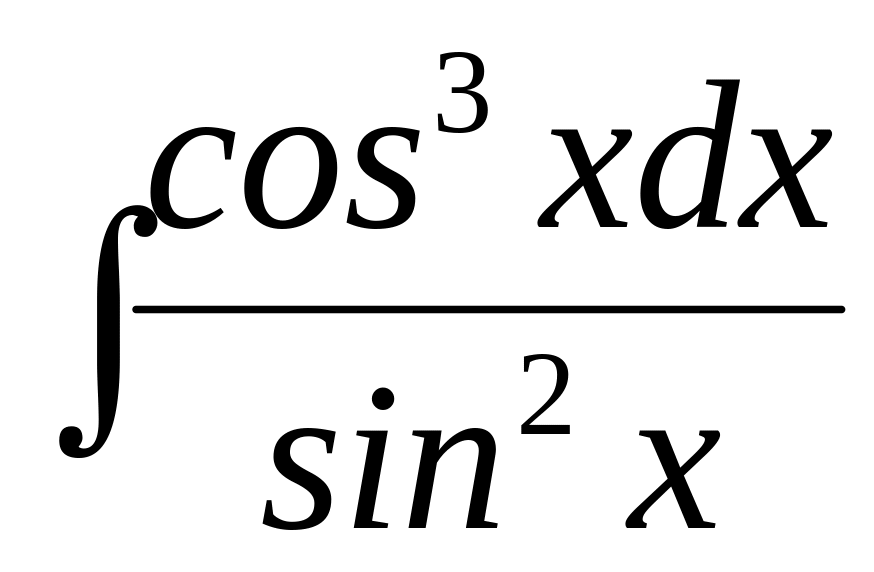 .
.
№ 81-100. Вычислить определенные интегралы:
а)
 ;
б)
;
б)
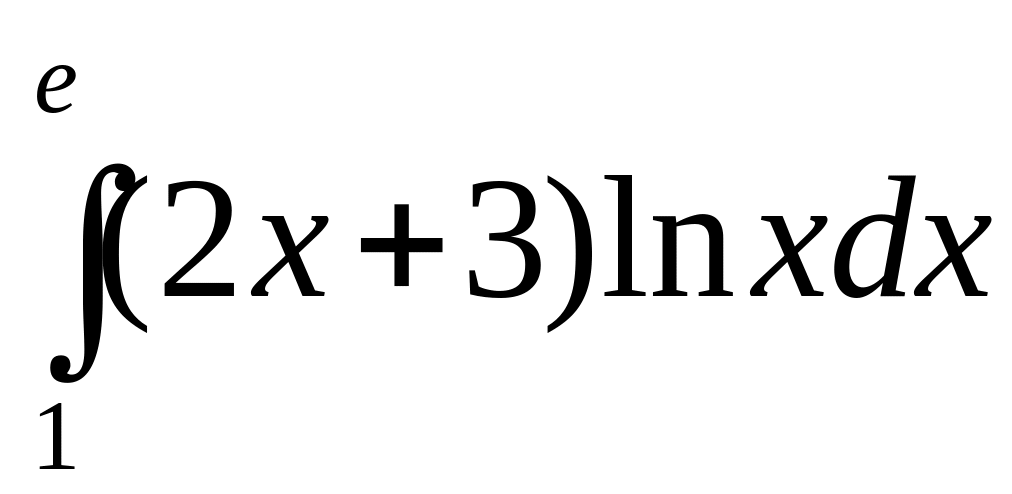 .
.
а)
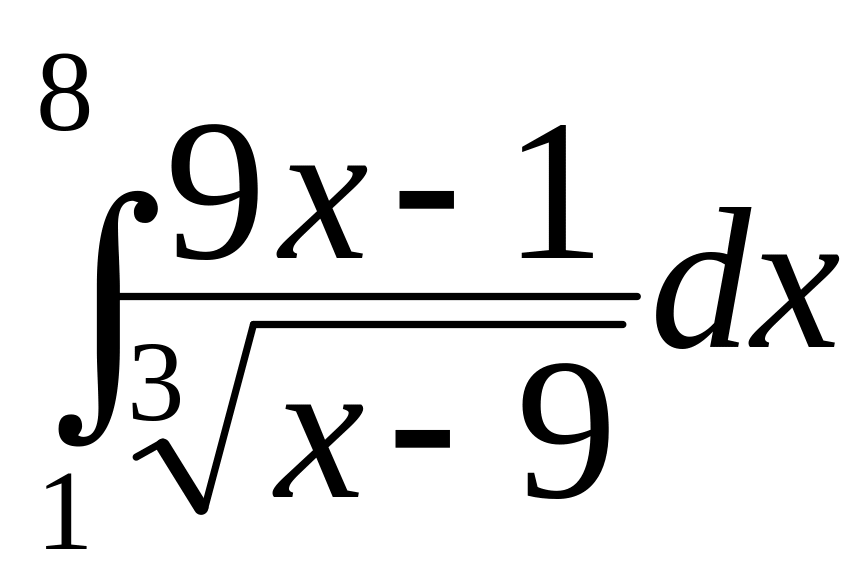 ;
б)
;
б)
 .
.
а)
 ;
б)
;
б)
 .
.
а)
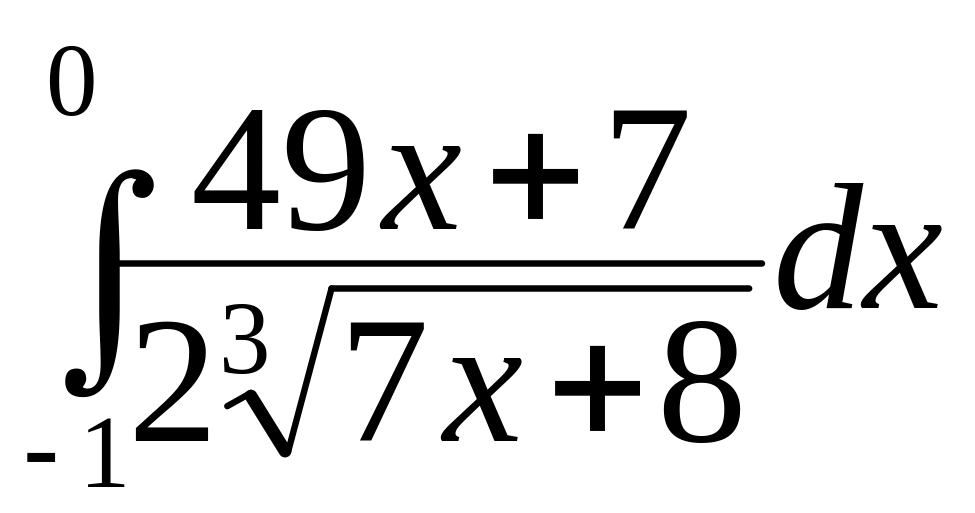 ;
б)
;
б)
 .
.
а)
 ;
б)
;
б)
 .
.
а)
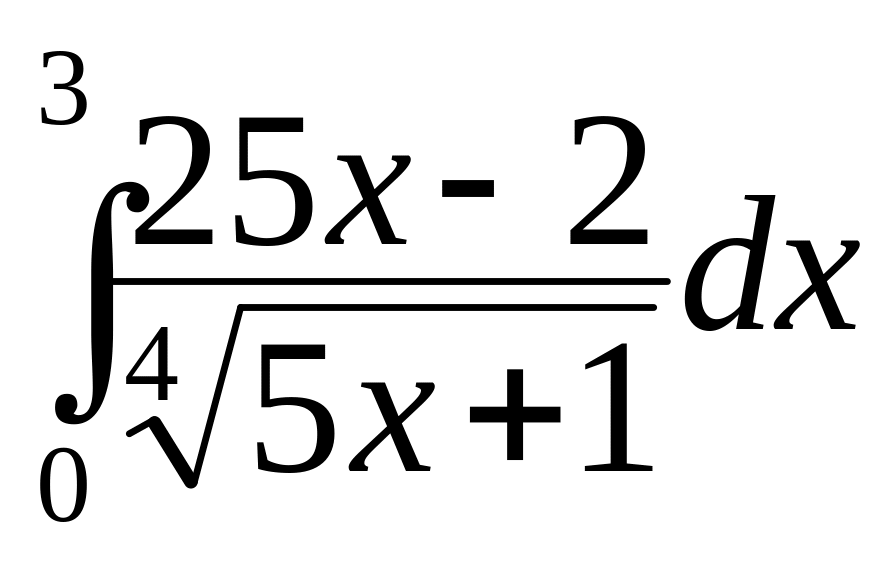 ;
б)
;
б)
 .
.
а)
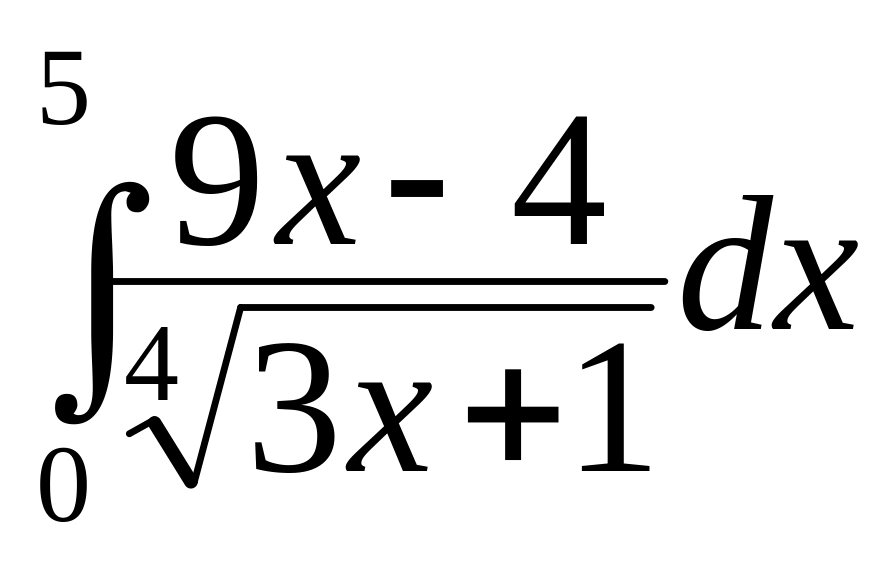 ;
б)
;
б)
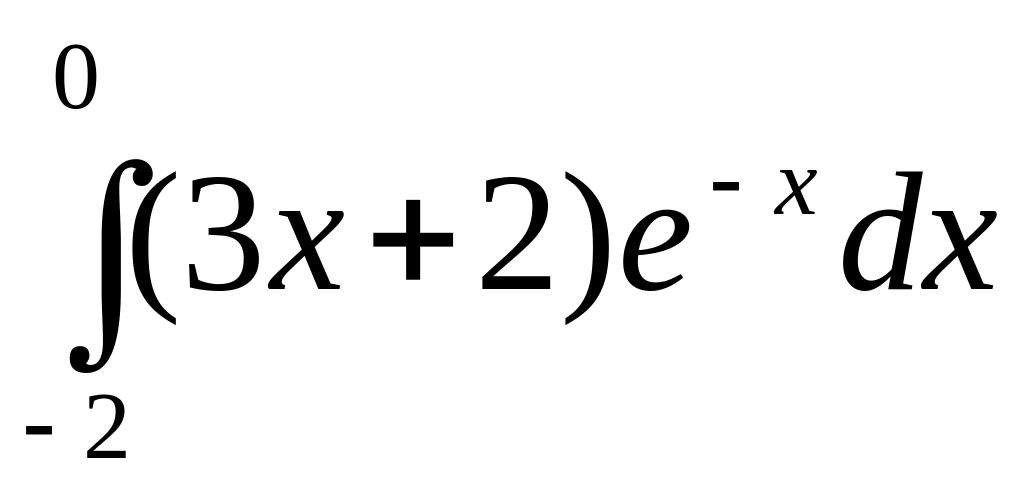 .
.
а)
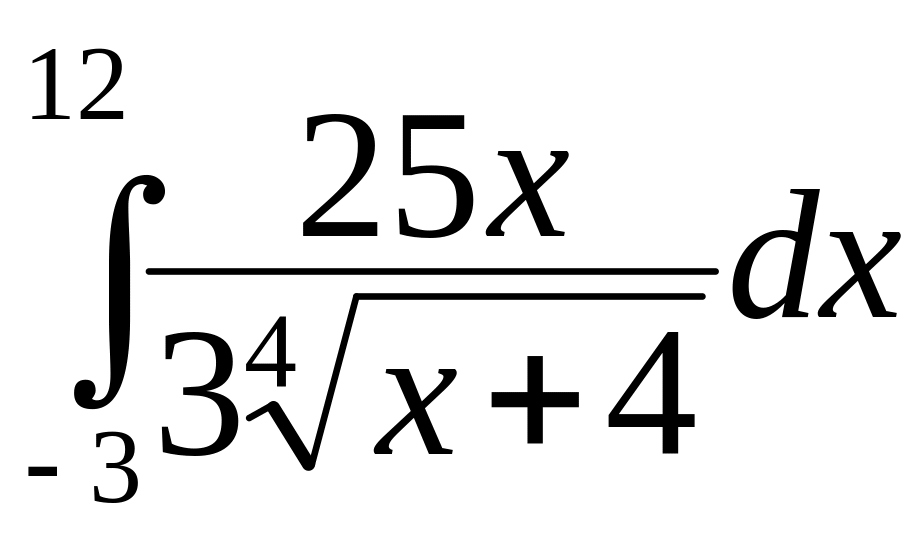 ;
б)
;
б)
 .
.
а)
 ;
б)
;
б)
 .
.
а)
 ;
б)
;
б)
 .
.
а)
 ;
б)
;
б)
 .
.
а)
 ;
б)
;
б)
 .
.
а)
 ;
б)
;
б)
 .
.
а)
 ;
б)
;
б)
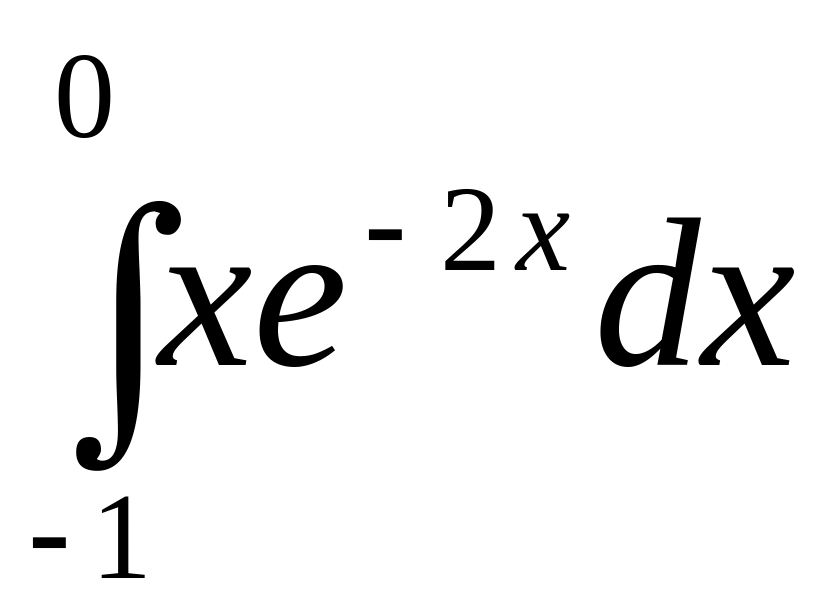 .
.
а)
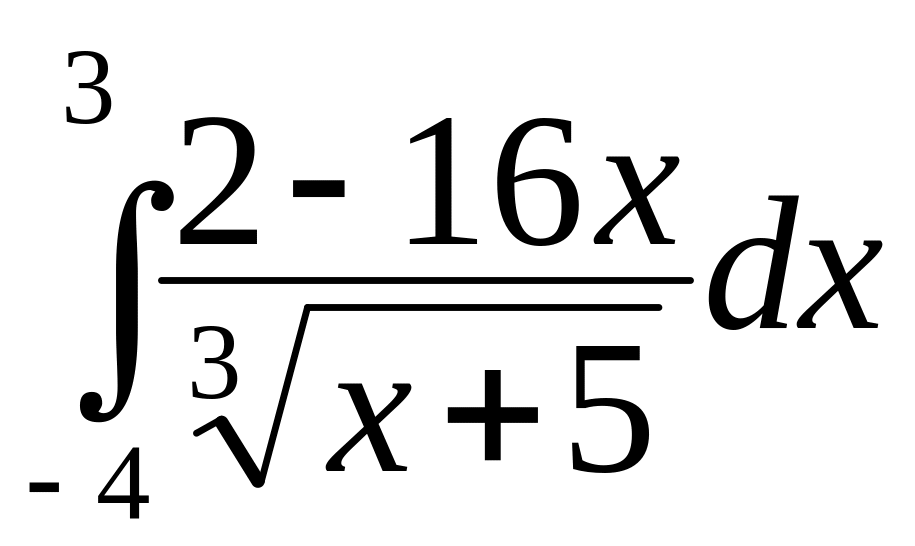 ;
б)
;
б)
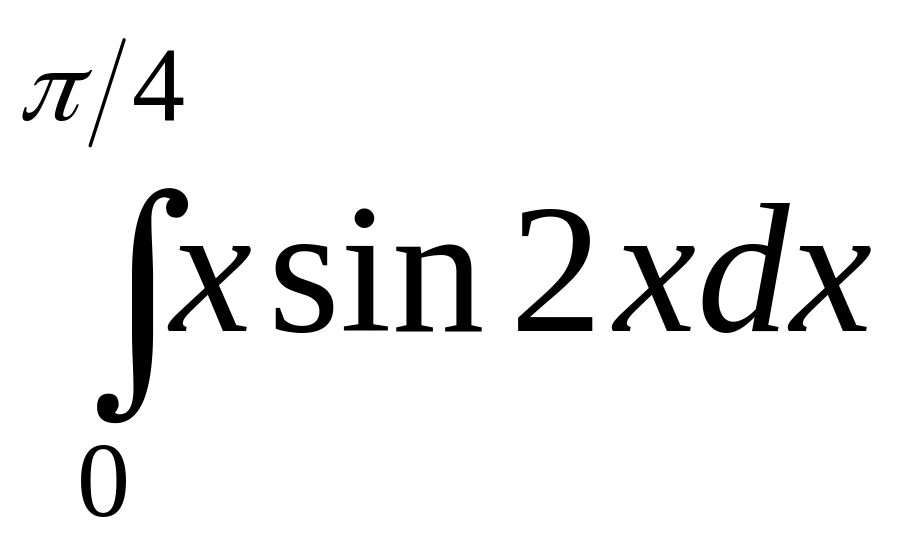 .
.
а)
 ;
б)
;
б)
 .
.
а)
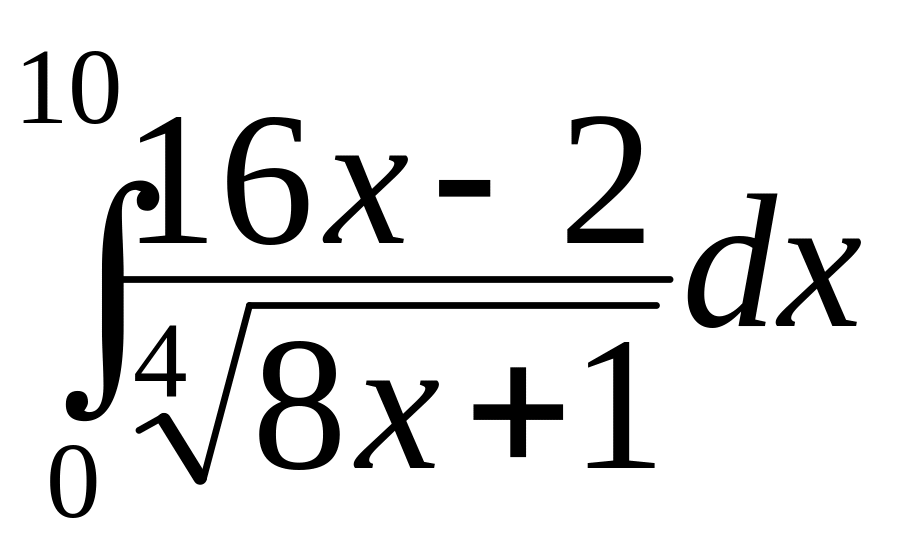 ;
б)
;
б)
 .
.
а)
 ;
б)
;
б)
 .
.
а)
 ;
б)
;
б)
 .
.
а)
 ;
б)
;
б)
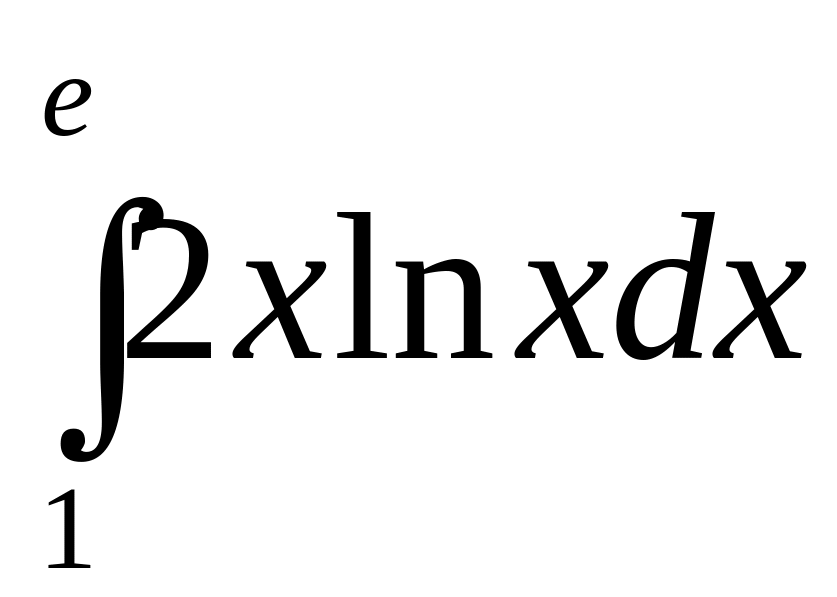 .
.
№ 101-120. Вычислить определенный интеграл с точностью до 0,001 путем предварительного разложения подынтегральной функции в ряд и почленного интегрирования этого ряда.
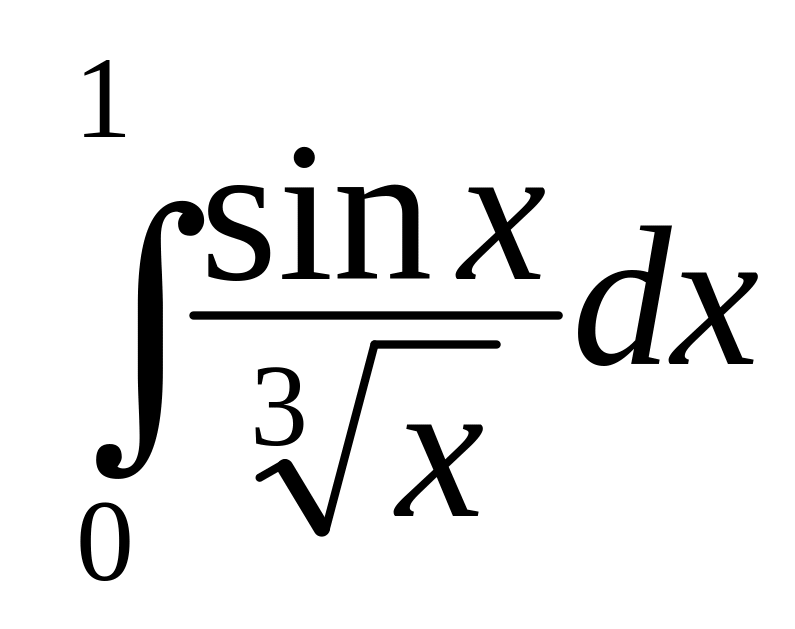 .
. .
.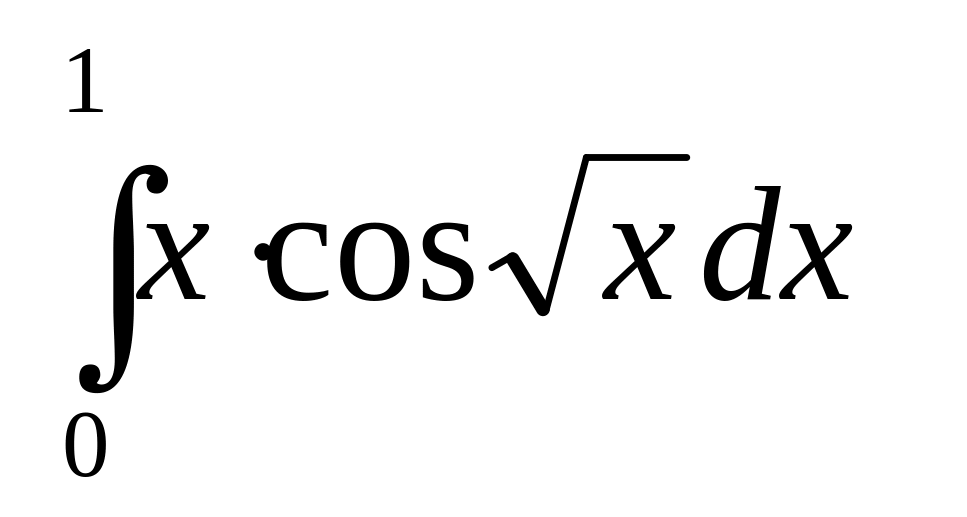 .
.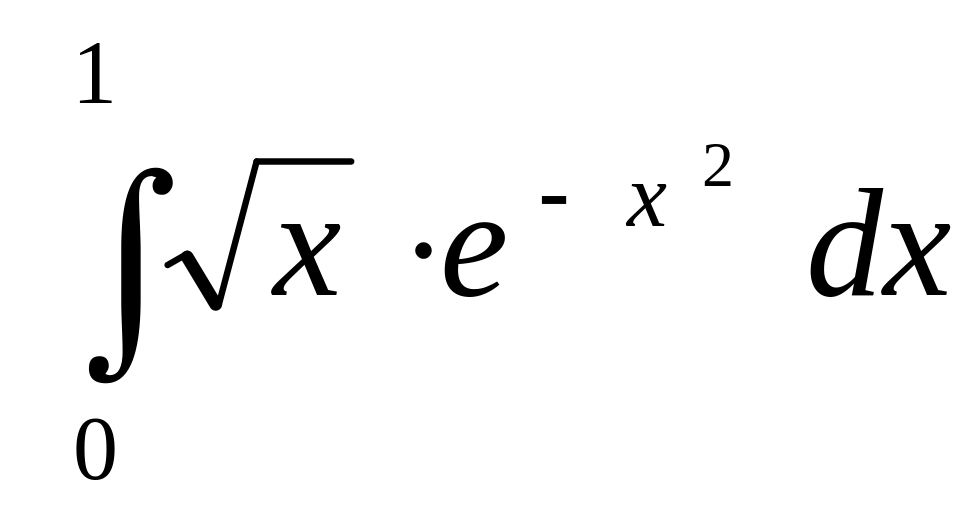 .
.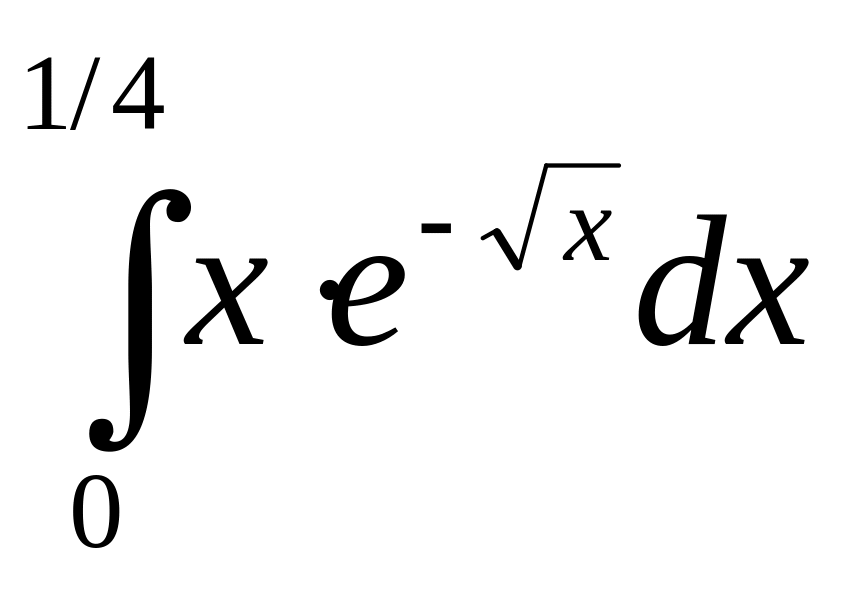 .
.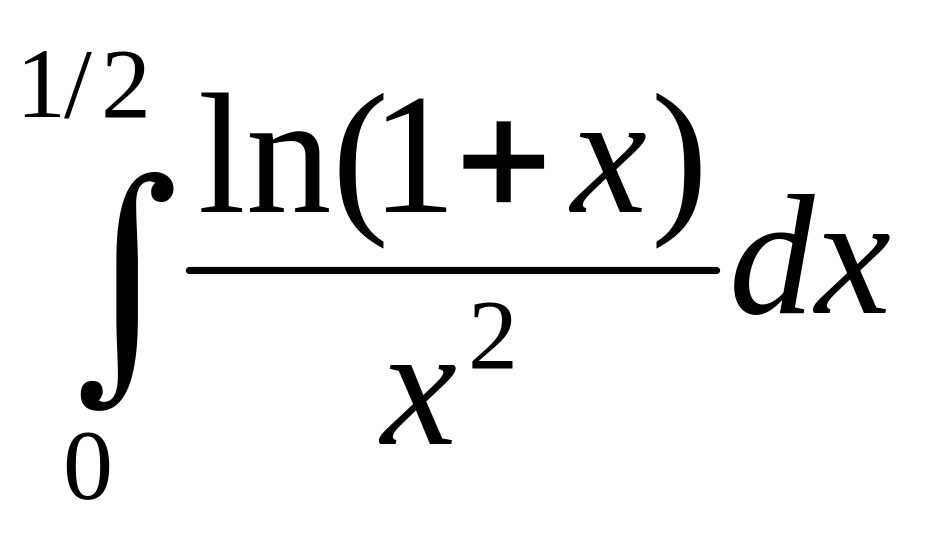 .
. .
. .
.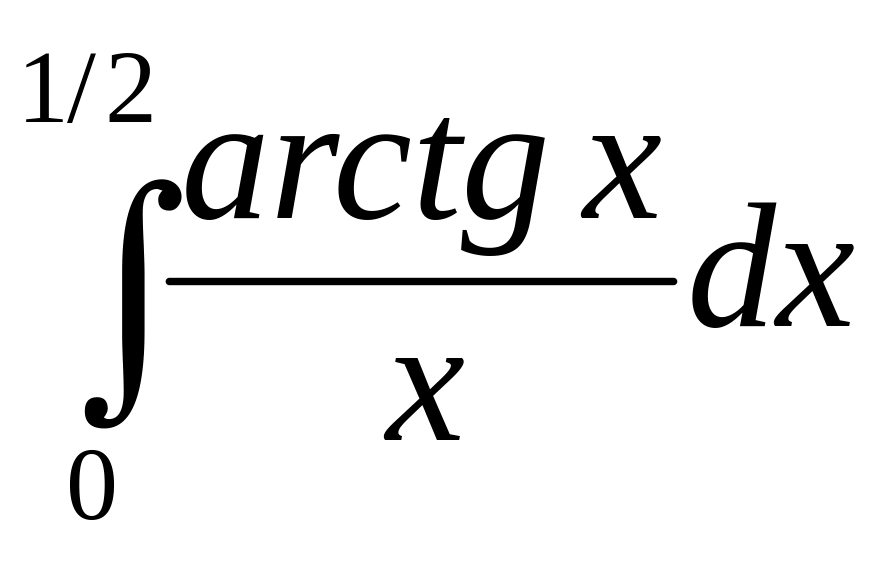 .
. .
. .
. .
. .
.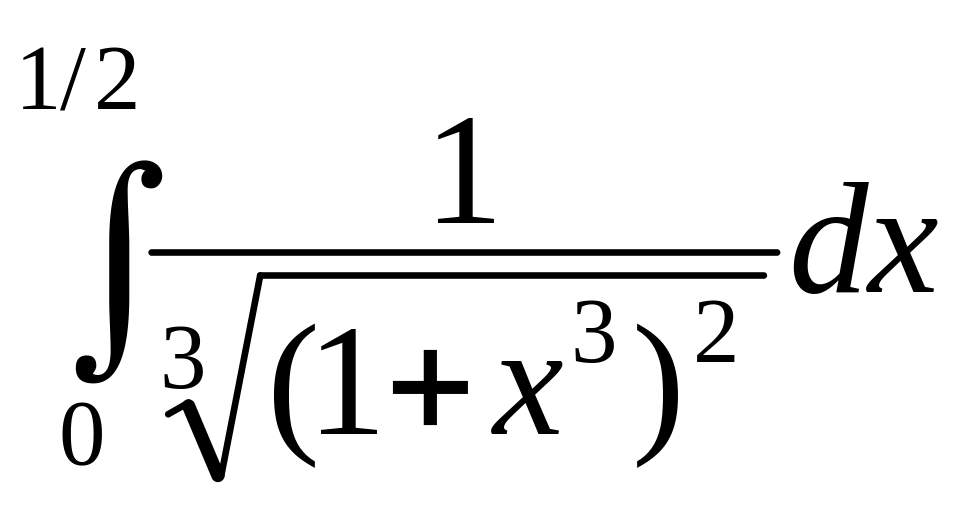 .
. .
. .
. .
. .
.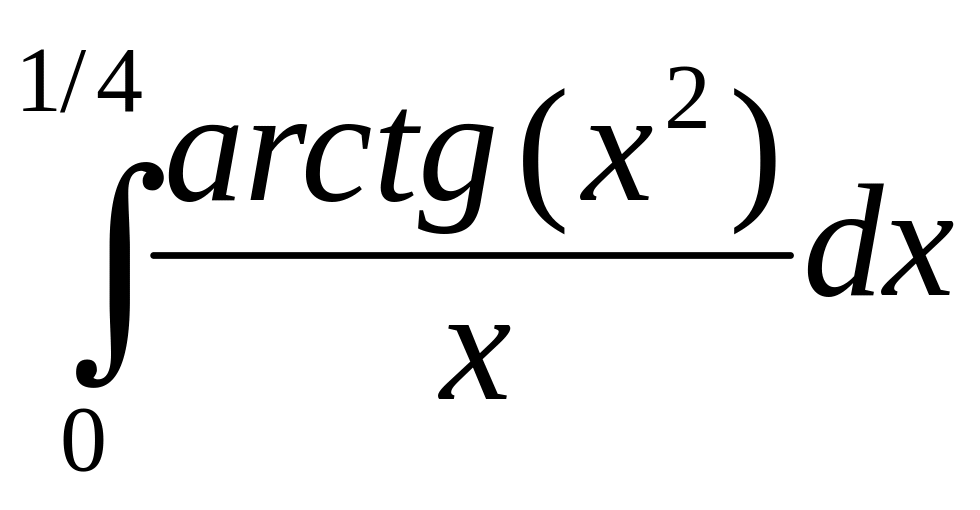 .
.
