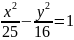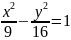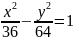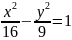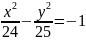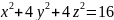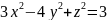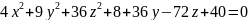Блок «Гипербола»

Задача 1

Составить уравнение гиперболы, фокусы которой расположены на оси абсцисс симметрично относительно начала координат, зная, кроме того, что:

• Её оси 2a=10 и 2b=8;

• Расстояние между фокусами 2c=10 и ось 2b=8;

• Расстояние между фокусами 2c=6 и эксцентриситет = ;

• Ось 2a=16 и эксцентриситет = ;

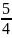• Уравнения асимптот 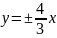и расстояние между фокусами 2c=20;

• Расстояние между директрисами равно и расстояние между фокусами 2c=26;

• Расстояние между директрисами равно и ось 2b=6;

• Расстояние между директрисами равно 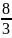и эксцентриситет = ;

• Уравнения асимптот и расстояние между директрисами

равно .

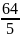Ответ:

• 

• 

• 

• 

• 

• 

• 

Задача 2

Составить уравнение гиперболы, фокусы которой расположены на оси ординат симметрично относительно начала координат, зная, кроме того, что:

• Её полуоси a=6, b=18 (буквой “a” мы обозначаем полуось гиперболы, расположенную на оси абсцисс);

• Расстояние между фокусами 2c=10 и эксцентриситет = ;

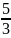• Уравнения асимптот 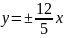и расстояние между вершинами равно 48.

• Расстояние между директрисами равно 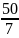и эксцентриситет = ;

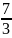• Уравнения асимптот и расстояние между директрисами

равно .

Ответ:

• 

• 

• 

• 

Задача 3

Установить, что каждое из следующих уравнений определяет гиперболу, и найти координаты её центра C, полуоси, эксцентриситет, уравнения асимптот и уравнения директрис:

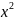1. 16 -9 -64x-54y-161=0

2. 9 -16 +90x+32y-367=0

3. 16 -9 -64x-18y+199=0

Ответ:

1)C(2;-3), a=3, b=4, 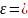5/3, уравнения директрис: 5х-1=0, 5х-19=0, уравнения асимптот: 4x-3y-17=0, 4x+3y+1=0;

2)C(-5;1), a=8, b=6, =1,25, уравнения директрис : x=-11,4 и x=1,4, уравнения асимптот: 3x+4y+11=0 и 3x-4y+19=0

3) C(2;-1), a=3, b=4, =1,25 , уравнения директрис: y= -4,2 , y=2,2 , уравнения асимптот: 4x+3y-5=0, 4x-3y-11=0

Задача 4

Фокусы гиперболы совпадают с фокусами эллипса . Составить уравнение гиперболы, если ее эксцентриситет =2.

Задача 5

Составить уравнение гиперболы, фокусы которой лежат в вершинах эллипса , а директрисы проходят через фокусы этого эллипса.

Блок «Поверхности 2-ого порядка»

Задача 1

Установить, что плоскость х-2=0 пересекает эллипсоид 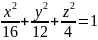по эллипсу.

Найти его полуоси и вершины.

Ответ: 3, ; (2;3;0), (2;-3;0), (2;0

Задача 2

Установить, что плоскость z+1=0 пересекает однополостный гиперболоид 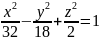по гиперболе.

Найти ее полуоси и вершины.

Ответ: 4, 3; (4;0;-1), (-4;0;-1)

Задача 3

Установить, что плоскость y+6=0 пересекает гиперболический параболоид 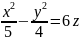по параболе.

Найти ее параметр и вершину.

Ответ: 15; (0;-6;- )

Упрощение уравнений кривых и поверхностей 2-го порядка.

Задача 1

Привести уравнение к каноническому виду, определить тип уравнения, установить какой геометрический образ определяет уравнение. Изобразить на чертеже оси первоначальной системе координат, оси других координатных систем, которые вводятся по ходу решения и геометрический образ определяющий данным уравнением.

1)

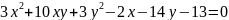
2)

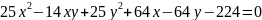
3)

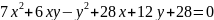
4)

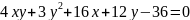
5)

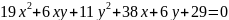
6)

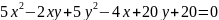
Задача 2

Определить какую поверхность задаёт следующие уравнения. Привести уравнение к каноническому виду и изобразить поверхность в прямоугольной декартовой системе координат.

1. 

2. 

3. 

4.