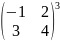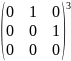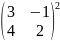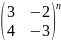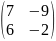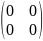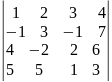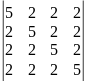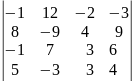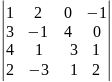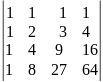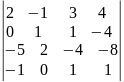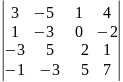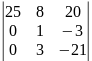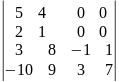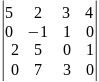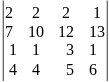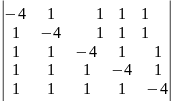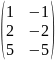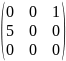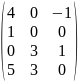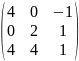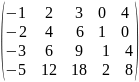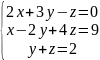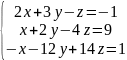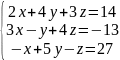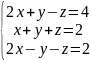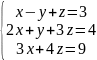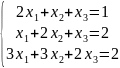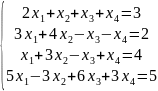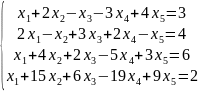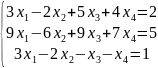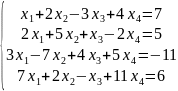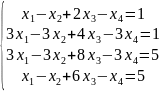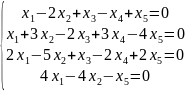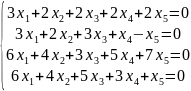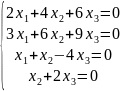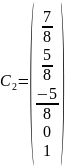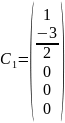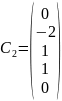- •Блок «Матрицы»
- •Блок «Вектор. Линейные операции над векторами» Деление отрезка в заданном отношении
- •Полярная система координат
- •Вектор. Координаты вектора.
- •Линейные операции над векторами
- •Скалярное произведение векторов
- •Векторное произведение векторов
- •Смешанное произведение векторов
- •Уравнение прямой на плоскости
- •Уравнение плоскости
- •Блок «Прямые в пространстве»
- •Блок «Парабола»
- •Блок «Эллипс»
- •Блок «Гипербола»
- •Блок «Поверхности 2-ого порядка»
- •Упрощение уравнений кривых и поверхностей 2-го порядка.
- •Квадратичные формы
- •Линейная зависимость и независимость векторов. Базис.
- •Евклидово пространство
- •Линейный оператор и его матрица
Блок «Матрицы»
Аnxn=(aij)
Сколько элементов расположено:
Над главной диагональю:
На главной диагонали:
Под главной диагональю:
Ответ:
На главной диагонали:
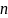
Под главной
диагональю: :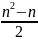
Над главной диагональю: :
Запишите матрицы А3x3 элементы, которых aik определяются по форме:
aik=i+k;
aik=i∙k
aik=(i-k)2
aik=i2k+ik2
Совпадают ли элементы этих матриц расположенных симметрично относительно главной диагонали.
Ответ:
A=
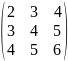
A=
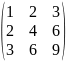
A=
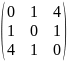
A=

Да, совпадают.
Для каких матриц Аmxn существуют A+AT
Ответ:
Для квадратных матриц.
Найти матрицу Х удовлетворяющую условию 3A+2X=E, где Е – единичная матрица 3-его порядка и матрица А равна:
А=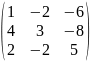
Ответ:
Х=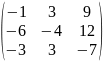
Известно, что A2x3∙Bmxn=С2x6. Найти m и n.
Ответ:
m=3; n=6
Даны матрицы A2x3, B3x1,C3x3. Существую ли произведения: АВ, ВA, AC, CA, ABC, CB, CBA, АСВ.
Ответ:
Существуют: АВ, AC,АСВ,СВ;
Не существуют: ВА, СА, АВС, СВА.
Найти сумму матриц А+В, разность А-В, произведение А∙В и В∙А, если существует:
А=
 В=
В=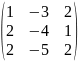
А=
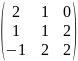 В=
В=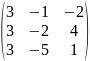
А=
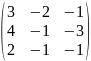 В=
В=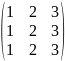
А=
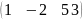 В=
В=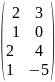
А=
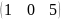 В=
В=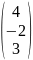
А=
 В=
В=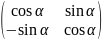
Найдите все матрицы перестановочные с матрицей:
А=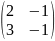
Вычислить степень приведённых ниже матриц:
Ответ:
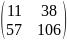


 в четной степени,
в нечетной степени- сама матрица.
в четной степени,
в нечетной степени- сама матрица.
Используя равенства:
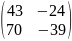 =
=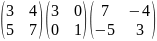 ;
;
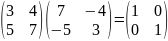 .
.
Вычислите
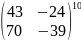
Докажите, что если матрицы А и В – перестановочные, то выполняется
(А+В)2=А2+2АВ+В2
(А+В)(А-В)=А2-В2
Верны ли эти равенства, если матрицы не являются перестановочными?
Ответ:
Если матрицы не перестановочные, равенство не выполняется.
Доказать, что если первая и вторая строки матрицы А равны, то первая и вторая строки матрицы АВ, так же равны.
Найдите f(A), если А=
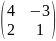
f(x) = x2-2x+5
f(x)=x2-5x+10
f(x)=(2x5-4x2+7)∙(x2-5x+10)+x+5
Ответ:
Вычислить определитель:
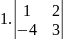 5.
5.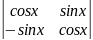
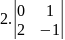 6.
6.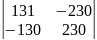
3. 7.
7.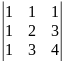
4.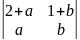 8.
8.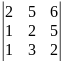
9.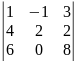
Найти x:
10.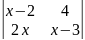 12.
12.
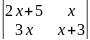
11.
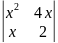
Доказать равенство:
13.
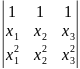 =
(
=
(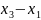 )(
)(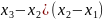
Ответ:
11
-2

2b-a
1
230
-1
-1
0
X=
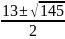
X=
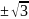
X=
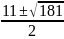
Доказано.
Вычислить определитель αA, если α=
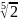 ,
а det
А5x5=3
,
а det
А5x5=3
Ответ: 6
Дано: числа 185; 518; 851делятся на 37.
Докажите что
определитель
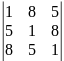 делится на 37 не вычисляя его.
делится на 37 не вычисляя его.
Вычислить определитель, раскладывая по элементам строки или столбцы, предварительно преобразовав их, используя свойства определителя.
Ответ:
900
297
150
-35
12
0
-110
Вычислить определитель, предварительно преобразовав его.
Ответ:
-300
30
-30
45
0
Найти матрицы обратные данным. Полученный результат проверить, используя определение обратной матрицы
А=
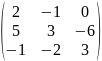
А=
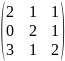
А=
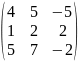
А=

Ответ:
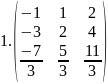
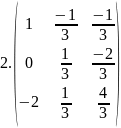
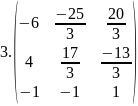
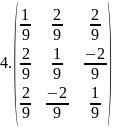
Найдите какой-либо базисный минор матрицы:
Проверить системы уравнений на совместность и в случае совместности данных систем уравнений решить их:
Методом Гаусса
Методом Крамера
Матричным методом
Ответ:
x=1 y=0 z=2
x=
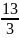 y= -
z= -
y= -
z= -
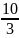
3. x=7 y=-1 z=-3
Решений нет
x=
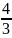 y=1
z=
-
y=1
z=
-
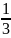
Ø
Решить системы уравнений Методом Гаусса;
Ответ:
Нет решений
x1=1 ; х2=0 ;х3=-1 ;х4=2
решений нет
x2=
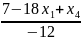 ;
х1=R;
x3=
;
х1=R;
x3=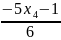 ;
х4=R
;
х4=R
x1=-8,x2=R,x3=2x2,x4=-3+x2
Нет решений
x1, x4 =R; x2=1+x1-x4; x3=1
Решить системы уравнений и найти нормированную фундаментальную систему решений:
Ответ:
3.НФСР – не существует. Решение тривиальное.
4. тривиальное решение.
Решить систему при всевозможных значениях параметра λ
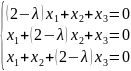
Ответ: Если λ≠1 и λ≠4, то Х1=Х2=Х3=0. Если λ=1, то Х1=-Х2-Х3, где Х2,Х3=R., если λ=4, то Х2=Х3; Х1=-3Х3, где Х3=R