4.1.3 Задача об использовании мощностей ("о загрузке оборудования")

j= 1,2,.., n – количество исходных нефтепродуктов;

k= 1,2,.., K – количество выпускаемых бензинов;

i= 1,2,.., m – количество анализируемых качественных характеристик;

Пусть завод располагает двумя видами станков, соответственно и 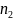штук каждого вида. Каждый из станков может производить 3 вида деталей с производительностью

Каждая партия деталей(по их видам) приносит доход, соответственно, 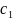, 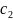и .

Заводу предписан план, согласно которому она должна производить в месяц (по видам деталей) не мене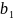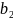е , и партий деталей.

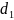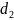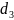Для исключения затоваривания торговли объем выпуска деталей не должен превышать (по видам деталей) , и партий. Кроме того, все без исключения станки должны быть загружены. Требуется так спланировать загрузку станков, чтобы суммарный месячный доход L был максимален.

Формальная постановка задачи.

Элементами решения являются не количество деталей по видам, а количество станков, занятых производством той или иной партии.

Математическая модель

Так как видов станков 2, а видов деталей 3, то удобнее элементы решения обозначить двумя индексами (первый - вид станка, второй - вид деталей): , , , , ,

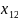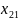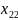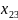
Выполнение планового задания:

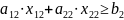
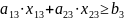
Отсутствие излишней продукции:

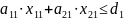
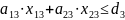
Ограничения, связанные с наличием станков и необходимостью их полной загрузки имеют вид:

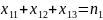
Суммарное количество партий деталей первого вида, произведенное всеми станками, будет равно 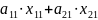и принесет доход ).

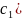Суммарный для завода месячный доход равен:

)

 

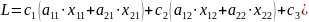Целевая функция

найти такие неотрицательные значения переменных х₁₁,х₁₂,х₁₃,x₂₁,x₂₂,x₂₃, которые должны удовлетворять ограничениям и одновременно обращали в максимум линейную функцию этих переменных, т.е.

Математическая модель представляет собой (4) и систему ограничений (1, 2, 3).

4.1.4 Задача "о поставке сырья"

 

№ предприятия	Склад № 1	Склад № 2	Склад № 3	Склад № 4	Склад № 5
	с11 с21 с31	с12 с22 с32	с13 с23 с33	с14 с24 с34	с15 с25 с35

Пусть имеются 3 предприятия, требующих, соответственно, а₁,а₂ и а₃ единиц сырья. Имеются 5 складов сырья, обеспечивающих стоимости поставок сырья, указанные в таблице.

Запас сырья на базах равен, соответственно, b₁,b₂,b₃,b₄ и b₅ единиц сырья.

Требуется составить такой план снабжения предприятий сырьем (с какой базы, куда и сколько сырья везти), чтобы потребности предприятий были обеспечены при минимальных расходах на сырье.

 

Формальная постановка задачи. Обозначим через x_ij количество сырья, получаемое i-м предприятием с j-го склада. Всего план будет состоять из 15 элементов решения:

 

x₁₁,x₁₂,x₁₃,x₁₄,x₁₅,x₂₁,x₂₂,x₂₃,x₂₄,x₂₅, x₃₁,x₃₂,x₃₃,x₃₄,x₃₅.

 

Ограничения-равенства по потребностям:

 

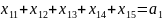
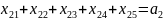
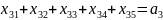
Ограничения-неравенства, вытекающие из возможностей складов:

 

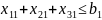
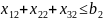
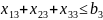
x₁₄ +x₂₄+x₃₄≤b₄;

x₁₅+x₂₅+x₃₅≤b₅.

 

С учетом таблицы, пользуясь знаком двойной суммы, получим суммарные расходы на сырье:

_{3 5}

L=∑ ∑(с_ij·x_ij)→ min. (7)

^{i=1 j=1}

Математическая модель представляет собой (7) и систему ограничений (5, 6), а поставленная задача сводится к нахождению неотрицательных значений элементов решения x_ij, при условии, что они удовлетворяют системе ограничений.