2 Страница

ВАРИАНТ 1,5,9,13,17,21,25,29

16. Сколько диагоналей у восьмиугольной усеченной пирамиды?

а) 20; б) 28 в) 40; г) другой ответ.

17. 7

Пусть V, R и G – соответственно число вершин, ребер и граней призмы. При условии, что R = 36, значение V + G равно…:

а) 32; в)36;

б) 34; г) 38

д)40

е) другой ответ.

18. Боковая поверхность правильной четырехугольной призмы равна 16 см² , а полная – 48 см² . Найдите высоту призмы.

а) 2 см; б) 4 см в) 1 см; г) другой ответ.

19. Найдите боковую поверхность правильной треугольной пирамиды, если сторона основания равна 2 см, а все двугранные углы при основании – 30º.

а)2 см²; б) 2 см²; в) см²; г) другой ответ.

20. Найдите площадь сечения куба ABCDA₁B₁C₁D₁ плоскостью, проходящей через ребро AB и середину ребра B₁C₁. Ребро куба равно 2 см.

а) см; б) 5 см; в) см; г) другой ответ..

21. Расстояние от вершин A, B, C параллелограмма ABCD, не пересекающего плоскость α, до плоскости α равны соответственно 18см, 11 см, 4 см. Найдите расстояние от вершины D до плоскости α.

а) 3см; б) см; в) 7 см; г) другой ответ.

22. Точки K, M и P – середины ребер AB₁ , BC₁ и BB₁ параллелепипеда ABCDA₁B₁C₁D₁. Значит, плоскость KMP параллельна плоскости

а) CA₁C₁:

б) A₁BC₁;

в) A₁CD₁;

г) ABC .

23. Основание тетраэдра SABC – правильный треугольник ABC, боковое ребро SA перпендикулярно плоскости основания, точка M – середина стороны BC. Найдите угол наклона прямой SM к плоскости ABC, если боковые ребра тетраэдра SA = , SB = SC =  .

а)60º, б)45º, в)30º, г) другой ответ.

24. Основанием пирамиды является равнобедренный треугольник ABC, у которого AC=AB=15см, BC=24см. Найдите объём пирамиды, если все боковые рёбра составляют с плоскостью основания угол 45^о..

25. Найдите высоту правильной треугольной пирамиды, сторона основания которой равна , а двугранный угол при боковом ребре 120º.

26. Дана пирамида MАВСD. В основании лежит ромб АВСD со стороной 4, , ВМ – высота равна . Найти угол наклона боковой грани МАD к плоскости основания.

27. В прямом параллелепипеде боковое ребро равно 10 см. Большая диагональ основания равна 9 см и образует с большей стороной основания, равной 7 см, угол, синус которого . Определите боковую поверхность параллелепипеда.

28. Сечение правильного тетраэдра проходит через середины двух ребер основания параллельно только одному боковому ребру. Найдите площадь сечения, если ребро тетраэдра равно 8.

ВАРИАНТ 2,6,10,14,18,22,26,30

16. Сколько диагоналей у семиугольной призмы?

а) 21 ;

б) 28 ;

в)14 ;

г)другой ответ .

17. Пусть V, R и G – соответственно число вершин, ребер и граней пирамиды. При условии, что V = 16, значение R + G равно…:

а) 32; в)46;

б) 36; г) 50

д)40

е) другой ответ.

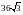18. Боковая поверхность правильной треугольной призмы равна см² , а полная – см² . Найдите высоту призмы:

а)3 см; б) 3 см; в) см; г) другой ответ.

19. Найдите боковую поверхность правильной четырехугольной пирамиды, если сторона основания равна 2 см, а все двугранные углы при основании – 45º.

а) см²; б) см²; в) 8 см²; г) другой ответ.

20. Найдите площадь сечения куба ABCDA₁B₁C₁D₁ плоскостью, проходящей через ребро AB и середину ребра СC₁. Ребро куба равно 4  см.

а) 10 см²; б) см²; в) 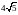см²; г) другой ответ.

21. Точки K, M и P – середины ребер AD , DC₁ и DD₁ параллелепипеда ABCDA₁B₁C₁D₁. Значит, плоскость KMP параллельна плоскости

а) CA₁C₁: б) AB₁C₁; в) ACD₁; г) AA₁C .

22. Расстояние от вершин A, B, C параллелограмма ABCD, не пересекающего плоскость α, до плоскости α равны соответственно 5 см, 12 см, 19 см. Найдите расстояние от вершины D до плоскости α.

а) см; б) 12 см; в) 6 см; г) другой ответ.

23. Основание пирамиды SABCD – ромб ABCD, в котором А = 60º и сторона равна 2. Боковые грани SAB и SAD перпендикулярны плоскости основания, ребро SС наклонено к плоскости ABC под углом 45º.Найдите объем пирамиды.

а) 4, б) 8, в) , г) другой ответ.

24. Основанием пирамиды является равнобедренный треугольник ABC, у которого AC=AB=30см, BC=36см. Найдите объём пирамиды, если все боковые рёбра составляют с плоскостью основания угол 45^о

25. Найдите высоту правильной треугольной пирамиды, сторона основания которой равна , а двугранный угол при боковом ребре 120º..

26. Дана пирамида MАВСD. В основании лежит ромб АВСD со стороной 4, , ВМ – высота пирамиды равна 2. Найти угол наклона боковой грани МАD к плоскости основания.

27. В прямом параллелепипеде боковое ребро равно 10 см. Большая диагональ основания равна 8 см и образует с большей стороной основания, равной 5 см, угол 60º. Определите боковую поверхность параллелепипеда.

28. В правильной четырехугольной пирамиде сторона основания равна 6, а угол наклона бокового ребра к плоскости основания равен arccos . Найдите площадь сечения, проходящего через сторону основания и середину высоты пирамиды.

ВАРИАНТ 3,7,11,15,19,23,27

16. Сколько диагоналей у шестиугольной усеченной пирамиды?

а) 12;

б) 18

в) 24;

г) другой ответ.

16. Пусть V, R и G – соответственно число вершин, ребер и граней призмы. При условии, что R = 36, значение V + G равно…:

а) 32; в)36;

б) 34; г) 38

д)40

е) другой ответ.

16. Боковая поверхность правильной четырехугольной призмы равна 48 см² , а полная – 56 см² . Найдите высоту призмы.

а) 6 см; б) 4 см в) 1 см; г) другой ответ.

16. Найдите боковую поверхность правильной треугольной пирамиды, если сторона основания равна 2 см, а все двугранные углы при основании – 60º.

а)2 см²; б) 2 см²; в) см²; г) другой ответ.

16. Найдите площадь сечения куба ABCDA₁B₁C₁D₁ плоскостью, проходящей через ребро AB и середину ребра B₁C₁. Ребро куба равно 6 см.

а) см; б) 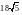см; в) 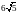см; г) другой ответ..

16. Расстояние от вершин A, B, C параллелограмма ABCD, не пересекающего плоскость α, до плоскости α равны соответственно 18см, 11 см, 4 см. Найдите расстояние от вершины D до плоскости α.

а) 11см; б) см; в) 7 см; г) другой ответ.

16. Точки K, M и P – середины ребер AB₁ , BC₁ и BB₁ параллелепипеда ABCDA₁B₁C₁D₁. Значит, плоскость KMP параллельна плоскости

а) CA₁C₁:

б) ABC;

в) A₁CD₁;

г) A₁BC₁ .

16. Основание тетраэдра SABC – правильный треугольник ABC, боковое ребро SA перпендикулярно плоскости основания, точка M – середина стороны BC. Найдите угол наклона прямой SM к плоскости ABC, если боковые ребра тетраэдра SA = , SB = SC =  .

а)60º, б)45º, в)30º, г) другой ответ.

16. Основанием пирамиды является равнобедренный треугольник ABC, у которого AC=AB=13см, BC=24см. Найдите объём пирамиды, если все боковые рёбра составляют с плоскостью основания угол 45^о..

17. Найдите высоту правильной треугольной пирамиды, сторона основания которой равна , а двугранный угол при боковом ребре 120º.

18. Дана пирамида MАВСD. В основании лежит ромб АВСD со стороной 4, , ВМ – высота равна . Найти угол наклона боковой грани МАD к плоскости основания.

16. В прямом параллелепипеде боковое ребро равно 10 см. Большая диагональ основания равна 9 см и образует с большей стороной основания, равной 7 см, угол, синус которого . Определите боковую поверхность параллелепипеда.

16. Сечение правильного тетраэдра проходит через середины двух ребер основания параллельно только одному боковому ребру. Найдите площадь сечения, если ребро тетраэдра равно 6.

ВАРИАНТ 4,8,12,16,20,24,28

16. Сколько диагоналей у девятиугольной призмы?

а) 54 ;

б) 27 ;

в)81 ;

г)другой ответ .

16. Пусть V, R и G – соответственно число вершин, ребер и граней пирамиды. При условии, что V = 14, значение R + G равно…:

а) 32; в)46;

б) 36; г) 50

д)40

е) другой ответ.

16. Боковая поверхность правильной треугольной призмы равна 18 см² , а полная – 36 см² . Найдите высоту призмы:

а) см; б) 2 см; в) см; г) другой ответ.

16. Найдите боковую поверхность правильной четырехугольной пирамиды, если сторона основания равна 2 см, а все двугранные углы при основании – 60º.

а) см²; б) см²; в) 8 см²; г) другой ответ.

16. Найдите площадь сечения куба ABCDA₁B₁C₁D₁ плоскостью, проходящей через ребро AB и середину ребра СC₁. Ребро куба равно 4  см.

а) 10 см²; б) см²; в) см²; г) другой ответ.

16. Точки K, M и P – середины ребер AD , DC₁ и DD₁ параллелепипеда ABCDA₁B₁C₁D₁. Значит, плоскость KMP параллельна плоскости

а)ACD₁ : б) AB₁C₁; в) CA₁C₁; г) AA₁C .

16. Расстояние от вершин A, B, C параллелограмма ABCD, не пересекающего плоскость α, до плоскости α равны соответственно 5 см, 12 см, 19 см. Найдите расстояние от вершины D до плоскости α.

а) см; б) 18 см; в) 6 см; г) другой ответ.

16. Основание пирамиды SABCD – ромб ABCD, в котором А = 60º и сторона равна 6. Боковые грани SAB и SAD перпендикулярны плоскости основания, ребро SС наклонено к плоскости ABC под углом 30º.Найдите объем пирамиды.

а) 64, б)36, в) , г) другой ответ.

16. Основанием пирамиды является равнобедренный треугольник ABC, у которого AC=AB=26см, BC=36см. Найдите объём пирамиды, если все боковые рёбра составляют с плоскостью основания угол 45^о

17. Найдите высоту правильной треугольной пирамиды, сторона основания которой равна , а двугранный угол при боковом ребре 120º..

18. Дана пирамида MАВСD. В основании лежит ромб АВСD со стороной 4, , ВМ – высота пирамиды равна . Найти угол наклона боковой грани МАD к плоскости основания.

16. В прямом параллелепипеде боковое ребро равно 8 см. Большая диагональ основания равна 8 см и образует с большей стороной основания, равной 5 см, угол 60º. Определите боковую поверхность параллелепипеда.

16. В правильной четырехугольной пирамиде сторона основания равна 12, а угол наклона бокового ребра к плоскости основания равен arccos . Найдите площадь сечения, проходящего через сторону основания и середину высоты пирамиды.