
- •Тест. Стереометрия. Вариант 1,7,13,19,25
- •Тест. Стереометрия. Вариант 2,8,14,20,26
- •В тетраэдре abcd вершина d проектируется на высоту ah основания abc. Следовательно, верно утверждение:
- •На каком из рисунков изображено сечение пирамиды плоскостью, проходящей через диагональ основания bd параллельно ребру sa?
- •Тест. Стереометрия. Вариант 3,9,15,21, 27
- •Тест. Стереометрия. Вариант 4,10,16,22,28
- •В тетраэдре abcd вершина d проектируется на высоту ah основания abc. Следовательно, верно утверждение:
- •Тест. Стереометрия. Вариант 5,11,17,23,29
- •Точки a,b,c и d не лежат в одной плоскости. Выберите верное утверждение:
- •Выберите верное продолжение фразы: проекция трапеции на плоскость при параллельном проектировании может быть
- •Через вершину прямоугольника abcd проведена прямая ak, перпендикулярная его плоскости. Какое из данных утверждений неверно?
- •Тест. Стереометрия. Вариант 6,12,18,24,30
- •В тетраэдре abcd вершина d проектируется на высоту ah основания abc. Следовательно, верно утверждение:
- •2 Страница
Тест. Стереометрия. Вариант 3,9,15,21, 27
Даны два утверждения:
1) если одна из двух параллельных прямых пересекает третью прямую, то и другая её пересекает;
2)если одна из двух прямых лежит в некоторой плоскости, а другая прямая пересекает эту плоскость, то эти две прямые скрещиваются.
Тогда
а) оба утверждения верны ; б) первое утверждение верно, а второе нет;
в) второе утверждение верно, а первое нет ; г) оба утверждения неверны .
В кубе ABCDA1B1C1D1 ребро равно 2. Расстояние от центра грани A1B1C1D1 до плоскости, проходящей через вершины В, D и С1 равно….
а)
 ; б)
; б)
 ; в)1
; г)
; в)1
; г)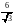 д)
д) .
.
В параллелепипеде ABCDA1B1C1D1 точки M и N – середины сторон A1B1 и B1C1 . Тогда прямые MC и AN:
а)пересекаются ; б)скрещиваются ; в) параллельны.
В тетраэдре ABCD, все ребра которого равны, вершина D проектируется в точку О на основание ABC. Точка E – середина ребра BC. Следовательно, прямые DO и AE:
а) параллельны; б) пересекаются; в) скрещивающиеся.
В тетраэдре ABCD ребра AD, BD, CD равны между собой, а вершина D проектируется на ребро AВ основания ABC. Следовательно, верно утверждение:
а) треугольник AВC – остроугольный ;
б) треугольник AВC – тупоугольный ;
в) треугольник AВC –прямоугольный ;
г) о виде треугольника AВC ничего сказать нельзя.
Точка A принадлежит окружности, AK – перпендикуляр к плоскости окружности, равный единице. AB – диаметр, BC – хорда окружности, составляющая с AB угол 45º. Радиус окружности равен 2. Найдите KC .
а)2 см; б) 5 см; в) 6 см; г) другой ответ.
Два равных прямоугольника с общей стороной 80 см и второй стороной 60 см образуют двугранный угол 60º. Найдите косинус угла между непересекающимися диагоналями прямоугольников.
а)
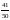 ,
б)
,
в)
,
б)
,
в) ,
г)
,
д) другой ответ.
,
г)
,
д) другой ответ.
в прямоугольном параллелепипеде ABCDA1B1C1D1 AB = 3, AD = 4, AA1 = 1. Найдите синус угла С1BDC.
а) ; б)
; б) ; в)
; в) ; г)
; г) д)другой
ответ.
д)другой
ответ.
Через вершину A треугольника ABC проведена плоскость α, параллельная BC. C1 α, CC1 α, CC1 , = 42 . M – точка пересечения медиан треугольника. MM1 α . Найдите MM1 .
а) 50 ; б) 28; в) 20; г) другой ответ.
Одна из граней многогранника пятиугольник. Какое наименьшее число граней может иметь многогранник?
а) 5; б) 6; в) 7; г) 10; д)25.
Точки M, N – середины рёбер AB и CC1 соответственно параллелепипеда ABCDA1B1C1D1. При пересечении параллелепипеда плоскостью ANM образуется: .
а)треугольник, б)четырёхугольник, в)пятиугольник, г) шестиугольник.
ABCD, AMNB, BNPC – квадраты. . O – середина стороны AD . Найдите угол между PD и NO.
а)60º, б)45º, в)30º, г) другой ответ.
Площадь полной поверхности прямоугольного параллелепипеда равна 76, а стороны основания равны 2 и 4. Найдите высоту параллелепипеда.
Основание тетраэдра SABC – правильный треугольник ABC, боковое ребро SA перпендикулярно плоскости основания, точка M – середина стороны BC. Найдите двугранный угол SBCA, если боковые ребра тетраэдра SA = 2, SB = SC = 2 .
Сечение куба ABCDA1B1C1D1 проходит через точку B и середины ребер AA1 и CC1. Найдите ребро куба, если площадь сечения равна
 .
.
