1 страница

Тест. Стереометрия. Вариант 1,7,13,19,25

1. Точки A,B,C и D не лежат в одной плоскости. Выберите верное утверждение:

а) прямая AB параллельна прямой CD;

б) прямая AB пересекает прямую CD;

в) прямая AC пересекает прямую BD;

г) прямые AB и CD – скрещивающиеся.

2. Сторона KM треугольника KMB принадлежит плоскости α. Точка P, не принадлежащая прямой KM, – проекция точки B на плоскость α. Точка N – середина MB. Выберите неверное утверждение:

а) прямые MP и NP пересекаются;

б) прямые MB и NP пересекаются;

в) прямые KB и NP пересекаются;

г) прямые KP и NP пересекаются.

3. Плоскость α, параллельная стороне BC треугольника ABC, пересекает стороны AB и AC в точках M и N соответственно. Найдите длину отрезка BC, если MN равен 6 см, а AM : MB = 3 : 5.

а) 16 см; б)4,8 см; в)12 см; г) другой ответ.

4. В тетраэдре ABCD вершина D проектируется на высоту AH основания ABC. Следовательно, верно утверждение:

а) ребра попарно перпендикулярны;

б)боковые ребра равны;

в) ребро AD перпендикулярно ребру BC;

г)все ребра тетраэдра равны.

5. Выберите верное продолжение фразы: проекция трапеции на плоскость при параллельном проектировании может быть

а) параллелограммом или трапецией;

б) только трапецией

в) отрезком или трапецией;

г)ромбом или трапецией.

6. Расстояние от некоторой точки до плоскости квадрата равно 4 см, а до каждой из его вершин – 6 см. Найдите диагональ квадрата.

а)2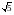 см; б) 5 см; в) см; г) другой ответ.

7. На каком из рисунков изображено сечение пирамиды плоскостью, проходящей через диагональ основания BD параллельно ребру SA?

8. Через вершину прямоугольника ABCD проведена прямая AK, перпендикулярная его плоскости. Какое из данных утверждений неверно?

а) KAAC; б)KDCD; в)KBCB; г)KCCB.

9. Расстояние от вершин A, B, C параллелограмма ABCD, не пересекающего плоскость α, до плоскости α равны соответственно 14 см, 11 см, 4 см. Найдите расстояние от вершины D до плоскости α.

а) 3см; б) 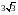см; в) 7 см; г) другой ответ.

10. Дан прямоугольный треугольник ABC ( угол C – прямой). Точка M не лежит в плоскости треугольника. Прямые MA, MB и MC составляют с плоскостью треугольника равные углы. Какое из данных утверждений верно?

а) плоскости MAB и ABC перпендикулярны:

б) плоскости MBC и ABC перпендикулярны;

в) плоскости MAC и MBC перпендикулярны;

г) условия а)–в) неверны.

11. Основание тетраэдра SABC – правильный треугольник ABC, боковое ребро SA перпендикулярно плоскости основания, точка M – середина стороны BC. Найдите угол наклона прямой SM к плоскости ABC, если боковые ребра тетраэдра SA = 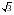, SB = SC =  .

а)60º, б)45º, в)30º, г) другой ответ.

12. Стороны основания прямоугольного параллелепипеда равны 6 м и 8 м, а угол между диагональю параллелепипеда и плоскостью основания равен 45°. Найдите длину диагонали параллелепипеда.

а) 20 м; б) 30 м; в) 10 м; г) м; д) 10 м

13. АВС – прямоугольный равнобедренный треугольник с гипотенузой AB = , , AМ – перпендикуляр к плоскости АВС, АМ = 2. . Найти величину двугранного угла МBCA .

14. АВСD – ромб со стороной 4, , ВМ – перпендикуляр к плоскости ромба и равен . Найти расстояние от точки М до прямой АD.

15. Найти расстояние от точки пересечения диагоналей куба до его ребра, если площадь поверхности куба равна 108.