2.2. Введение в квадратичное программирование

В настоящее время имеется достаточно много данных об успешном применении моделей ЛП в условиях нелинейности. При этом только необходимо отвечать на вопрос: «В каких случаях линейный или линеаризованный вариант является адекватным отображением нелинейного процесса?» Известно, что достаточно хорошее линейное приближение не удается построить в тех случаях, когда диапазон допустимых решений достаточно широк, а мы не имеем представления о характере оптимального решения.

Пусть, например, фирма находится на начальном этапе разработки модели перспективного планирования. Нам интуитивно понятно, а специалисты знают наверняка, что даже опытному бизнесмену трудно дать точный и детальный прогноз оптимальных объемов производства фирмы и роста занимаемой доли рынка на предстоящие 10 и более лет. Обращение к экономико-математическому моделированию в такой ситуации обусловлено тем, что вероятность грубой ошибки очень высока при использовании только интуитивных соображений в стремлении оценить влияние экономических факторов на широких временных горизонтах. Здесь если затраты производства и выручка от реализации зависят от объема операций нелинейно, а это зачастую так и есть, то линеаризованные догадки могут оказаться недостаточными для получения надежных прогнозов.

Если в задаче (2.1), (2.2) хотя бы одна из функций нелинейная, то и задача является задачей нелинейного программирования (НП). Среди таких задач наиболее глубоко исследованы задачи выпуклого программирования. В результате их решения определяется минимум выпуклой или максимум вогнутой функции, заданной на выпуклом замкнутом множестве.

Среди задач выпуклого программирования в наибольшей мере изучены задачи квадратичного программирования. Результатом решения таких задач является экстремум квадратичной функции при условии, что ее переменные удовлетворяют некоторой системе линейных неравенств или уравнений, либо некоторой системе, содержащей как линейные неравенства, так и линейные уравнения.

Отдельными классами задач математического программирования выступают задачи целочисленного, параметрического, дробно-линейного, стохастического и динамического программирования. Ими в рамках данного пособия мы не будем заниматься, а заинтересованного читателя отсылаем к учебной литературе по исследованию операций и математическому программированию.

2.2.1 Задачи квадратичного программирования (кп)

Приведем примеры нелинейных оптимизационных задач в экономике.

1) Нелинейная задача оптимального планирования производства. Пусть прибыль от изготовления единицы продукции и удельные нормы расхода ресурсов зависят от объема выпуска. Прибыль от производства единицы продукции определяется разностью между ценой и себестоимостью. Цена либо устанавливается предприятием-монополистом, либо определяется условиями конкурентного рынка. Себестоимость, а также удельная норма расхода ресурсов на единицу продукции определяются объемами ее производства.

Положим, что предприятие производит видов продукции из видов ресурсов. Через обозначим вектор валовых выпусков, а через 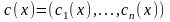– вектор прибыли. Удельные нормы расхода го ресурса зададим вектором . Тогда задача оптимального планирования производства формализуется следующим образом:

Найти (2.17)

при ограничениях (2.18)

где имеющееся количество ресурсов го вида – скалярное произведение векторов.

Здесь если функции и являются линейными, то имеем задачу квадратичного программирования.

В большинстве случаев нелинейности, которые необходимо отобразить в оптимизационных математических моделях относятся к одной из двух категорий:

• эмпирически наблюдаемые соотношения, такие, например, как непропорциональные изменения затрат, выхода продукции и показателей качества;

• выведенные математически или установленные руководством правила поведения.

Примеры первого вида можно наблюдать на очень многих производствах, например, когда прирост выпуска продукции отстает от роста затрат труда, а темпы роста количества отходов его обгоняют. Примером второго вида могут служить счета, оплачиваемые гражданами за коммунальные услуги.

Нелинейности «встраиваются» в оптимизационные задачи в огромном числе случаев. Приведем еще несколько примеров.

2) Выручка от реализации продукции. Спрос на продукцию компании чаще всего зависит от цен реализации. Чем ниже цена, тем больше объем реализации, даже несмотря на аналогичную ценовую политику, проводимую конкурентами. Очевидно, что выручка от реализации продукции на изменяется пропорционально цене. Последнее обстоятельство должно быть отражено с помощью нелинейного слагаемого в целевой функции многопродуктовой модели. Пусть, например, объем реализации, зависящий от цены . Тогда выручка от реализации есть произведение . Положим, что на рассматриваемом интервале изменения цены функция объема реализации от цены линейна, то есть . Тогда слагаемые в целевой функции, относящиеся к выручке от реализации, являются квадратичными относительно управляющей переменной и имеют вид: .

3) Размер многопродуктового заказа. Часто бывает так, что оптовый покупатель пополняет свои запасы, заказывая у одного и того же поставщика одновременно несколько видов продукции. Тем самым достигается экономия на транспортных затратах, расходах по оформлению документации и скидке на размер заказа, предоставленной поставщиком. Эта ситуация может рассматриваться службой логистики на основе использования модели математического программирования большой размерности, в которой затраты на пополнение запасов являются нелинейной функцией нескольких переменных – размеров заказов отдельных продуктов.

4) Уровень страховых запасов. В большинстве моделей математического программирования, используемых для общефирменного планирования, длительность отрезков планового периода редко составляет менее трех месяцев и часто превышает год. В таких динамических «многопериодных» моделях обычно предусматривается наличие страховых запасов, которые должны компенсировать колебания недельного объема реализации товаров. Один из подходов, применяемых в этих моделях, заключается в следующем.

Уровень страхового запаса предполагается зависимым как от прогнозируемого объема реализации, так и от степени использования производственных мощностей, обусловленных этим прогнозом. Пусть, например, максимально возможный недельный объем производства рассматриваемого продукта – производственная мощность, прогнозируемый средненедельный объем его реализации, уровень страхового запаса продукта, где число недель, зависимое от коэффициента использования производственных мощностей . Положим для примера, что планово-финансовый отдел принял следующую формулу для расчета :

Тогда уровень страхового запаса представляет собой квадратичную функцию прогнозируемого средненедельного объема реализации, имеющую вид:

Этот уровень может входить как в ряд ограничений модели, так и в целевую функцию.

5) Выбор портфеля ценных бумаг. Специалисты по финансовым рынкам считаю одной из главных своих задач разработку математических моделей, помогающих определить наилучший набор акций, облигаций и других ценных бумаг на выделенную сумму. Такими моделями учитывается оценка как ожидаемой прибыли от приобретения предлагаемого набора бумаг, так и связанного с этим риска или вероятностного колебания действительных значений прибыли. Рассмотрим самый простой вариант подобной модели.

Пусть доля имеющихся средств, выделяемых для приобретения ценных бумаг вида . Положим, что прибыль к концу планового периода на каждую тысячу рублей, вложенную в бумаги , характеризуется двумя показателями: фактическая прибыль (случайная величина), ожидаемая прибыль. Положим далее, что задано условие: ожидаемая прибыль на тысячу рублей инвестиций для всего набора ценных бумаг должна быть не ниже заданной величины . Тогда ограничения этой модели имею вид:

(2.19)

Риск учитывается с помощью целевой функции. Пусть выбирается таким образом, чтобы минимизировать дисперсию фактической прибыли при выполнении условий (2.19). Тогда целевая функция представляет собой следующую квадратичную форму:

где обозначает ковариацию прибыли для ценных бумаг вида и вида .

В более сложных вариантах модель может содержать ограничения, относящиеся к структуре набора ценных бумаг. Модели могут быть динамическими и включать различные показатели риска.

Как следует из вышесказанного, множество разнообразных обстоятельств приводит к нелинейным формулировкам ограничений и целевых функций в оптимизационных задачах экономики. Ниже рассмотрим базовый метод их решения.