Глава 2. Оптимизационные задачи экономики

Целью настоящей главы является научить студента, будущего экономиста с высшим университетским образованием, формализации многочисленных оптимизационных задач экономики с помощью соответствующего аппарата математического программирования, реализованного в вычислительных математических средах и программных продуктах Майкрософт, а также анализу полученных решений.

2.1. Основы линейного программирования (лп)

2.1.1 Формализация задачи

В параграфе рассмотрена задача ЛП – задача о наиболее рациональном использовании ограниченных ресурсов, описан симплекс-метод ее решения, показана его реализация в программных продуктах.

Фундаментальные результаты по линейному программированию были опубликованы в 1939 году в Ленинградском государственном университете Л.В. Канторовичем. Как таковой термин «линейное программирование» появился в 1951 году в работах американцев Дж. Б. Данцига – создателя симплекс-метода – и Т. Купманса.

Прямая задача ЛП формулируются следующим образом:

максимизировать функцию

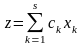(2.1)

при условиях

(2.2)

Двойственная задача ЛП имеет вид:

минимизировать функцию

(3.3)

при условиях

(2.4)

В задачах (2.1), (2.2) и (2.3), (2.4) представлены следующие переменные и показатели: показатель при й переменной в целевой функции прямой задачи; количественное значение й переменной в прямой задаче; показатель затрат го ресурса в расчете на единицу измерения й переменной; количество ресурсов го вида, учитываемых при решении прямой задачи; объективно обусловленная оценка единицы ресурса го вида; количество учитываемых при решении прямой задачи ресурсов; 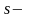количество основных переменных в прямой задаче. Говорят, что решить оптимизационную задачу – это значит найти ее оптимальный план.

Задачи (2.1), (2.2) и (2.3), (2.4) являются взаимодвойственными. Их построение проводится по строго определенному правилу, которое мы коротко изложим.

Если в прямой задаче ЛП ищется максимум целевой функции, то в обратной – минимум. Это становится ясным, если считать, что в первом случае речь идет о получении прибыли, а во втором о затратной части производственной программы. Каждому му условию прямой задачи соответствует неизвестная двойственной задачи. Если ограничения в прямой задаче определены неравенствами со знаком « », то в двойственной задаче они будут содержать знак « ». Количественные значения ограничений ( ) прямой задачи выступают в качестве показателей при переменных в целевой функции двойственной задачи. Показатели ( ) при переменных в целевой функции прямой задачи фигурируют в качестве количественных ограничений в двойственной задаче. Матрица коэффициентов затрат ресурсов на единицу измерения переменных в двойственной задаче является транспонированной по отношению к матрице коэффициентов затрат ресурсов на единицу измерения переменных прямой задачи. Такова формальная сторона дела. Теперь приведем простой и наглядный пример постановки задачи ЛП. Подобными примерами изобилуют учебные пособия.

Пример. Фирма производит три вида продукции. Для изготовления каждого из них необходимо затратить рабочее и машинное время, а также сырье. В таблице 2.1 приведены затраты указанных ресурсов на производство единицы продукции.

Таблица 2.1 – Удельные затраты ресурсов (пример)

Вид продукции	Рабочее время час/ед. продукции	Машинное время час/ед. продукции	Сырье, ед. сырья/ ед. продукции
1 2 3	2 2 4	4 3 2	2 3 1

Необходимо определить, сколько и какого вида продукции следует производить для максимизации суточного валового дохода фирмы от реализации, если в расчете на одни сутки имеются следующие ресурсы: рабочее время – 24 ч, машинное время – 12 ч, сырье – 18 ед. Единица первого вида продукции стоит 16 $, второго – 20 $, третьего – 18 $.

Мы специально сформулировали задачу в таком виде, что она уже практически формализована. Можно сходу записать ее в форме (2.1)-(2.2), обозначив через число единиц продукции каждого вида.

(2.5)

Ясно, что по смыслу задачи ответ должен быть целочисленным, однако специальные методы целочисленного программирования здесь не рассматриваются. Ответ предлагается округлить.

В соответствии с правилом формирования двойственной задачи имеем:

(2.6)

В задаче (2.6) переменные – это оценки (удельные цены) ресурсов. Двойственная задача ставится в предположении, что производитель, по каким-либо причинам пропуская данный производственный цикл и распродавая производственные ресурсы, не хотел бы остаться «в проигрыше». Он желает на единицу выпуска каждого производственного процесса «заработать» не меньше, чем в случае действительной реализации этих процессов. Целевая функция реализует желание покупателя – заплатить за приобретаемые ресурсы как можно меньше.

Далее нам следует перейти к рассмотрению расширенной задачи ЛП, для чего запишем выражения (2.1), (2.2) в матричном виде:

(2.7)

Здесь имеется в виду, что строка, а столбец. Сопоставление (3.7) с (2.1), (2.2) позволяет видеть матрицу, векторы и их размерности.

Преобразуем теперь ограничения в виде неравенств в ограничения-равенства. Это необходимо для нахождения так называемого базисного допустимого решения. Базисное решение – это то, которое содержит ненулевые составляющие для такого числа переменных, которое равно строчной размерности системы ограничений. Остальные переменные в базисном решении равны нулю. если такое решение еще и допустимо, то оно и называется базисным допустимым решением. Для построения такого решения в каждое неравенство введем дополнительную переменную . Этим переменным можно придать экономический смысл. Так, если имеющийся объем го ресурса, то неиспользованная часть этого ресурса. Таким образом, число дополнительных переменных в расширенной задаче ЛП равно , а их общее число вместе с первоначальными равно . В расширенной задаче переменных всегда больше, чем ограничений. Таким образом, ограничения в виде равенств представляют собой недоопределенную систему линейных алгебраических уравнений.

Основные результаты линейного программирования даются следующими утверждениями, доказательство которых можно увидеть, например, в [1].

Утверждение 1. Если ограничения имеют допустимое решение, то они имеют и базисное решение.

Утверждение 2. Область допустимых решений является выпуклым множеством.

Утверждение 3. Базисные допустимые решения соответствуют вершинам выпуклого множества.

Утверждение 4. Если целевая функция имеет конечный минимум, то по крайней мере одно оптимальное решение является базисным.

Приведенные утверждения означают, что при поиске оптимального решения задачи ЛП в допустимой области можно ограничиться целенаправленным перебором базисных допустимых решений – вершин выпуклого многогранника. Симплекс-метод, разработанный Дж. Б. Данцигом, как раз и представляет собой вычислительную алгебраическую процедуру такого перебора.