2.3. Общее правило замены переменной интегрирования

Чтобы вычислить неопределённый интеграл по переменной x, можно сделать замену х на новую переменную z, связанную с переменной х дифференцируемой функцией, имеющей обратную дифференцируемую функцию. Для этого нужно выразить через z всё подынтегральное выражение (включая dx). После вычисления интеграла по переменной z нужно сделать обратную замену к переменной х.

Пример (замена переменной интегрирования)

рекомендуемая замена: x=2sint,  ;

т.к.cost >0 при ;

график заменяющей функции дает возможность убедиться в существовании обратной функции:

так как функция , является монотонной, то существует обратная функция ;

обратную замену нужно совместить с упрощением тригонометрического выражения, для этого удобно использовать прямоугольный треугольник:



Ответ:

2.4. Метод интегрирования по частям (Опишите метод интегрирования по частям)

Этот метод интегрирования выполняется по формуле интегрирования по частям, которая имеет следующий вид:

Формула интегрирования по частям,

где u(x), v(x) — дифференцируемые функции.

 Исходным является правило дифференцирования произведения:

. 

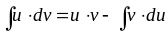Формулу интегрирования по частям эффективно применять, если интеграл является более простым по сравнению с интегралом .

Примеры (интегрирование по частям)

1)

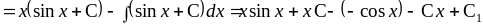
заметим, что при вычислении функции постоянную интегрирования можно не

учитывать;

2) = ;

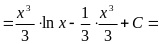3)

2.5. Основные типы интегралов, которые вычисляются с помощью формулы интегрирования по частям

C помощью формулы интегрирования по частям рекомендуется вычислять неопределенные интегралы перечисленных ниже типов.

I.	Обобщение: где — целый многочлен степени n=1,2,3,…
II.	III.
IV. «Круговые интегралы» (интегралы, приводящиеся к себе): ; .

Пример (вычисление «кругового

;

интеграл свелся к самому себе (так называемый «круговой интеграл»); записываем начало и конец выкладок и решаем уравнение относительно исходного интеграла:

;

этот интеграл часто используется в приложениях, поэтому он внесен в таблицу как дополнительный.

6. Упражнения для самостоятельной работы

1)	2)	3)
4)	5)	6)
7)	8)	9)
10)	11)	12)
13)	14)	15)
16)	17)	18)
19)	20)

Ответы к упражнениям для самостоятельной работы

1) (использовать формулу
2)	3)	4)
5)	6)	7)
8)	9)	10)
11)	12)	13)
14)	15)	16)
17)	18)	19)
20)

К началу параграфа