2. Основные свойства пределов.

1. . Предел алгебраической суммы равен сумме пределов слагаемых

2. . Предел произведения переменных величин равен произведению их пределов.

3. 3

4. 

5. 

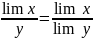
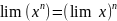
3. Предел функции в точке.

Даны две переменные величины x и y связанные функциональной зависимостью y = 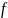(x). Рассмотрим вопрос о пределе функции при условии, что задан предел её аргумента.

Если при x a (x стремится к a), функция (x) b, то говорят, что предел функции (x) в точке x=a равен b и пишут 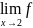(x) = b (рис. №1)

Опр.№2: Число b называется пределом функции (x) в точке a, если для всех значений x, достаточно близких к a и отличных от a, значит функции (x) сколько угодно мало отличаются от числа b. (рис. №1)

п. Найти

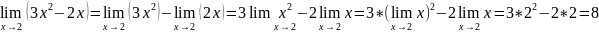
4. Приращение аргумента к приращению функции.

Если аргумент функции 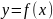изменяется от значения x до нового 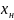, то разность 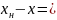Δx – называется приращением аргумента и обозначают символом Δх [читают: дельта икс] y = 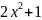(рис.№2)

Функция при изменении аргумента принимает новые значения 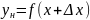т.е. приращение функции 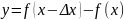Δ

п. Найти приращение аргумента и функции , если аргумент х изменяется от 1 до 1,02.

(рис. №2)

Решение: 1) Находим приращение аргумента Δх = 1,02 – 1 = 0,02;

2) Находим значение функции при старом значении аргумента, т.е. х = 1; y =

3) Находим значение функции при новом значении х = 1 + 0,002 = 1,02;

;

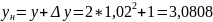5)Найдём Δy = 3,0808 -3 = 0,0808

II способ: Δy = 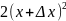+ 1; 2(

Δ y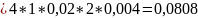

Контрольная работа: «Проверка вычислительных навыков»

Iв. 1) Упростить:

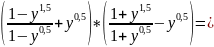
2)

IIв. 1)

2)

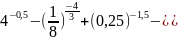
5) Понятие непрерывности функции.

Опр.№1: Функция 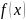называется непрерывной в точке , если а) эта функция определена в точке

б) приращение функции в точке стремится к нулю при Δx 0 т.е. 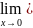График непрерывной функции представляют линию без разрыва.

Опр.№2: Функция называется непрерывной на отрезке [a,b], если она непрерывна в каждой точке этого отрезка. п. 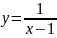Данная функция терпит разрыв при х=1

п. Найти

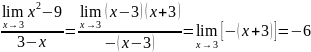
6) Предел функции на бесконечности.

Опр.: Число A называется пределом функции y = на бесконечности (или при x стремящимся к бесконечности) если для всех достаточно больших по модулю значений аргумента x соответствующее значение функции сколько угодно мало отличается от A

Из рис. №2 видно, что координаты изображающие значение функции сколько угодно мало отличаются от числа A=2, для любых больших x.

п. Найти 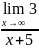: Решение: при 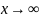значенатель x + 5 так же , а обратная ему величина 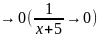. Следовательно, произведение , если

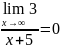
п. Пример на неопределенность вида :

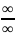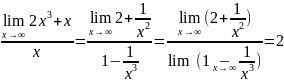
Решение: в этом примере числитель и знаменатель не имеют предел, т.к. возрастают. Для этого разделим числитель и знаменатель почленно на 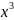(наивысшая степень в данном примере) т.к. 1/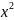 и 1/ при стремится к нулю.

Замечательные пределы:

1. Первый замечательный предел:

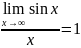
2. Второй замечательный предел:

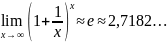
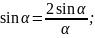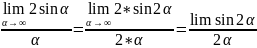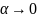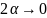п. Найти , если , то , тогда ;

п.

Предел функции

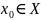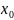Пусть функция определена на некотором промежутке X и пусть точка или . Составим из множества X последовательность точек: сходящихся к . Значения функции в этих точках также образуют последовательность:

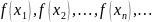
• Число A называется пределом функции в точке , если для любой сходящейся к последовательность значений аргумента , соответствующая последовательность значений функций сходится к числу A.

Это описывает так: .
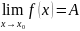