1.Геометрический смысл производной

Геометрическая интерпретация производной, впервые данная в конце XVII в. Лейбницем, состоит в следующем: значение про­изводной функции 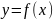в точке равно угловому коэффи­циенту касательной, проведенной к графику функции в той же точке (см. рис. 99), т.е. 

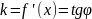.  (1) Таким образом, если функция  в точке   имеет производную, то график этой функции в точке с абсциссой   имеет касательную, и, наоборот, если в некоторой точке с абсциссой  существует касательная к графику, то при этом значении   существует производная. Иначе говоря, существование касательной к кривой   в некоторой точке с абсциссой  необходимо и достаточно для существования производной   в точке .

Геометрический смысл производной, выраженный равенством (1), дает наглядное представление о производной, позволяет проследить за ее изменением при движении точки М по кривой и дает возможность геометрически определить значение производной при данном значении  .

Из равенства (1) следует, что для нахождения углового коэффициента касательной к кривой в точке 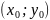нужно найти производную   и подставить в неё вместо абсциссу точки касания: .

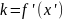Пусть дана непрерывная функция . Тогда в любой точке 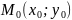, принадлежащей графику этой функции (рис. 102), можно провести касательную и нормаль (прямую, перпендикулярную касательной в точке касания). Уравнение касательной, как всякой прямой, проходящей через данную точку в данном направлении, имеет вид 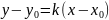, где 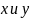– текущие координаты. Но 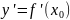и уравнение касательной запишется так:

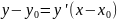. (2)

Уравнение нормали запишется в виде

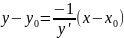. (3)

2.Механический смысл производной

Механическое истолкование производной было впервые дано И.Ньютоном. Оно заключается в следующем: скорость движения материальной точки в данный момент времени равна производной пути во времени, т.е.

.

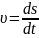Таким образом, если закон движения материальной точки задан уравнением 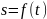, то для нахождения мгновенной скорости точки в какой-нибудь определённый момент времени нужно найти производную и подставить в неё соответствующее значение t. Для определённости будем считать, что путь измеряется в метрах, а время – в секундах.

3. Производная второго порядка и её механический смысл

Производную от данной функции часто называют первой производной (или производной первого порядка). Очевидно, что производная также является функцией, и если она дифференцируема, то от неё, в свою очередь, можно взять производную, которую называют второй производной (или производной второго порядка) и обозначают , .

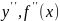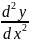Производной третьего порядка (или третьей производной) называют производную от второй производной. Её обозначают .

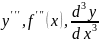Например, для функции имеем , , .

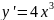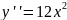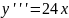Вообще производной n-го порядка от функции ) называется производная от производной 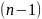-го порядка. Её обозначают: 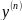, ,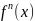 . Таким образом, производную -го порядка можно найти последовательным дифференцированием данной функции.

Рассмотрим механический смысл производной второго порядка.

Пусть тело движется прямолинейно по закону . Как известно, скорость 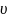движения тела в данный момент времени равна производной пути по времени, т.е. .

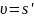Если тело движется неравномерно, то скорость с течением времени изменяется и за промежуток времени 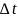получает приращение 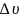. В этом случае величина отношения 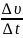, показывающая изменение скорости в единицу времени, называется средним ускорением в промежутке времени от .

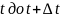Пусть 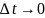; тогда а среднее ускорение стремится к величине, которая называется ускорением в данный момент времени t. Следовательно, ускорение движущегося тела представляет собой скорость изменения его скорости.

Обозначив ускорение через 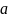, получим:

Таким образом, ускорение прямолинейного движения тела в данный момент равно второй производной пути по времени, вычисленной для данного момента.

В этом и заключается механический смысл второй производной.