Практическое построение жордановой нормальной формы матрицы
При получении такой задачи сразу
становится ясным то, что требуется найти
собственные значения матрицы (оператора).
Кстати, саму матрицу можно рассматривать
как оператор в пространстве столбцов.
Таким образом, нужно построить
характеристический многочлен и
постараться найти его корни. Считая
формально, что работаем в комплексном
пространстве, утверждаем, что все корни
суть собственные значения оператора.
Далее, возникает вопрос определения
размеров и количества жордановых клеток
для данного собственного значения. Для
этого введет величину
означающую число жордановых клеток
размерности
для собственного значения
.
Легко видеть (глядя на схему корневого
базиса), что размер клетки – это высота
соответствующего столбца в базисе,
т.е., размерность порождаемого им
циклического подпространства. Тогда
,
,
,
. . . . . . . .
,
. . . . . . . . .
,
.
Заменяя значения
,
,
на выражения (9.12), получим
,
,
,
. . . . . . . .
,
. . . . . . . . .
,
.
Ясно, что общей формулой является следующая:
.
где
– дефекты соответствующих операторов
(матриц). Учитывая соотношение между
рангом и дефектом
,
,
и тот факт, что ранги считать проще,
получаем формулу для
,
описывающую то же число посредством
вычисленных рангов матриц (операторов).
Именно:
.
Пример 9.25. Построить ЖНФ матрицы А, а также ее собственные и корневые подпространства,
.
Построим характеристический многочлен этой матрицы:
.
Отсюда видно, что собственными
значениями будут
и
,
причем первое трехкратное а второе
однократное. Это значит, что корневое
подпространство
имеет размерность 3, а
имеет размерность 1 и заведомо совпадает
с собственным подпространством. Найдем
сначала собственные подпространства.
Для этого решаем уравнение
.
Задавая вектор х матричным образом
в виде
и используя матрицу
с
,
а затем с
получаем две однородные системы линейных
алгебраических уравнений, общее решение
которых и дает представление о
соответствующих собственных
подпространствах. Строя фундаментальные
системы решений, выписываем подпространства
в виде линейных оболочек ФСР. Итак, для
:
Решая систему методом Гаусса в итоге получим общее решение:
Тогда ФСР, например, такая:
.
И собственное подпространство для
получается таким:
.
При этом
.
Интересно то, что уже сейчас можно представить ЖНФ матрицы А. Действительно, в силу малой размерности можно представить конфигурацию его корневого базиса, а именно:
Первый этаж составляют базисные векторы собственного подпространства. Их всего два, поэтому должны существовать векторы высоты 2. Поэтому нарисуем ЖНФ.
.
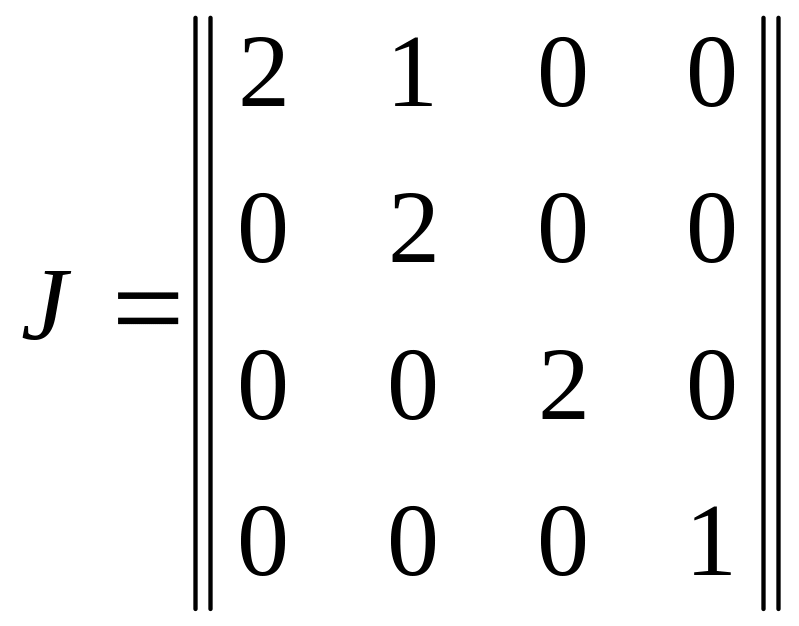В ней присутствует одна клетка Жордана второго порядка и одна первого порядка для , а для лишь одна клетка первого порядка.
Получим собственное подпространство для . Имеем:
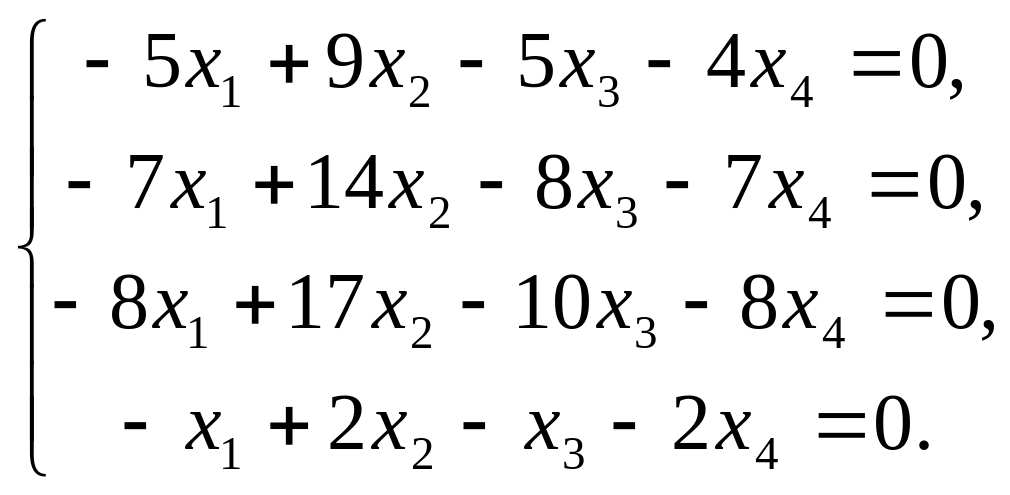
Решая систему, находим:
Откуда ФСР есть
и собственное подпространство для
таково:
.
С ним же совпадает, как было сказано, и соответствующее корневое подпространство.
Для того, что найти корневое подпространство для требуется решить уравнение
.
Возведем во вторую степень матрицу
и запишем соответствующую однородную
систему уравнений:
.
Тогда, очевидно, получим систему вида:
.
Это система ранга 1, поэтому общее решение должно иметь размерность 3, что вполне согласуется с теорией.
ФСР:
.
.
Если бы пришлось пользоваться
формулой для подсчета количества клеток,
то это уместно делать только для
.
Тогда вычислим
.
Но
,
,
.
В итоге получаем, что
.
Значит, будет лишь одна клетка первого
порядка для
,
и тогда остается лишь одна клетка второго
порядка. Хотя можно подсчитать и
.
Для этого потребуется знать
,
поэтому
.