ЕВКЛИДОВЫ ПРОСТРАНСТВА
Введение основного понятия
В произвольных абстрактных линейных пространствах над числовыми полями отсутствует возможность проведения измерений, как-то: длины вектора, расстояния между векторами и т. д. Это все при том, что в пространствах направленных отрезков подобные измерения возможны. Отсюда напрашивается вывод о необходимости введения некоторого универсального инструмента, с помощью которого измерения можно было бы осуществлять. Вспомним, что метрические понятия в пространствах направленных отрезков оказалось возможным выразить через понятие скалярного произведения. Но ведь само скалярное произведение определяется с помощью длины вектора и угла между направленными отрезками, чего в абстрактных пространствах как раз и нет. Решение задачи лежит в аксиоматизации свойств скалярного произведения направленных отрезков и переносе полученных аксиом в абстрактное вещественное пространство.
Определение 8.1. Пусть
произвольное вещественное линейное
пространство. Тогда скалярным
произведением в Х назовем
отображение
,
удовлетворяющее следующим аксиомам:
1.
;
2.
;
3.
;
4.
;
.
Пример 8.1. Очевидно, что обычное скалярное произведение направленных отрезков удовлетворяет этому определению.
Пример 8.2. Пусть
,
тогда для векторов
и
определим скалярное произведение
формулой
.
Легко проверить, что все аксиомы
выполняются.
Пример 8.3. Пусть, как в примере 8.2,
,
и заданы положительные вещественные
числа
.
Тогда скалярное произведение в этом же
пространстве определим формулой
.
Пример 8.4. Пусть
.
Для произвольных функций
и
скалярное произведение можно определить
формулой
.
Из предложенных аксиом легко получить ряд следствий, именно:
1.
;
2.
;
3.
;
4.
;
.
Наконец, для любых
и
имеем:
5.
,
для любых линейных комбинаций векторов
пространства Х. Для доказательства
последнего следствия можно использовать
математическую индукцию.
Определение 8.2. Евклидовым
пространством
называется вещественное линейное
пространство с введенным в нем скалярным
произведением.
Из этого определения следует, что приведенные примеры 8.1 – 8.4 одновременно представляют и евклидовы пространства, первые три из которых конечномерные, а последнее бесконечномерно. Как и ранее, будем в дальнейшем работать только с конечномерными евклидовыми пространствами.
Ортогональность
Из определения скалярного произведения
легко следует, что
.
В самом деле, например,
.
Но здесь интересен общий случай.
Определение 8.3. Пусть
– евклидово пространство и
.
Вектор
называется ортогональным к вектору
,
если
.
Ясно, что тогда и вектор
оказывается ортогональным вектору
.
Таким образом, это бинарное отношение
симметрично. Отношение ортогональности
часто обозначают
.
Лемма 8.1. Вектор, ортогональный к каждому вектору евклидова пространства, равен нулю.
Действительно, ведь тогда он ортогонален себе и по четвертой аксиоме обязан равняться нулю.
Следствие. Если
,
то
.
Определение 8.4. Система векторов называется ортогональной, если она состоит из одного ненулевого вектора или векторы ее составляющие попарно ортогональны.
Следующий результат связывает понятие ортогональности с понятием линейной независимости, что очевидно может иметь далеко идущие последствия.
Теорема 8.1. Ортогональная система, не содержащая нулевых векторов, линейно независима.
Доказательство. Случай
одноэлементной системы тривиален. Пусть
теперь задана ортогональная система
.
По определению здесь
для
,
,
и
.
Докажем линейную независимость системы
по
критерию ЛНЗ. Составим линейную комбинацию
векторов системы и приравняем ее нулю:
.
Умножим обе части равенства скалярно
на вектор
.
Получим
.
Тогда по четвертой аксиоме скалярного
произведения получается, что
.
Ясно, что в качестве множителя можно
взять любой
-й
вектор системы и показать, что
.
Таким образом, по критерию ЛНЗ
удостоверяемся в линейной независимости
системы
.
Определение 8.5. Вектор евклидова пространства называется нормированным, если его скалярный квадрат равен единице.
Любой ненулевой вектор можно
нормировать, т.е. перейти к коллинеарному
нормированному вектору. Действительно,
пусть
.
Тогда для
вектор
оказывается нормированным. Множитель
называется нормирующим множителем.
Определение 8.6. Система называется нормированной, если каждый вектор в ней нормирован.
Определение 8.7. Ортогональная и нормированная система называется ортонормированной.
Определение 8.8. Базисная
ортонормированная система называется
ортонормированным базисом. Сокращение
– ОНБ. Если
– ОНБ, то
.
(8.1)
Хотя пока неизвестен факт существования ортонормированных базисов, можно сформулировать два простейших свойства этого объекта.
Теорема 8.2. Пусть – ОНБ в . Тогда справедливы следующие утверждения:
1.
Если
,
то
;
2.
Система
является ОНБ тогда и только тогда, когда
,
где
,
а
скалярное произведение этих векторов
определяется формулой
.
Доказательство 1
.Умножая
скалярно обе части выражения
на вектор
,
,
и используя определение ОНБ, получаем
требуемое.
Доказательство 2 . Необходимость. Следствие 5 и определение сразу дают формулу скалярного умножения.
Достаточность. Пусть теперь
скалярное произведение задано указанным
в теореме способом. Тогда вектор
в данном базисе имеет координатную
строку, в которой все компоненты, кроме
-ой
равны нулю, а
-я
компонента равна единице. Поэтому
оказывается справедливой формула (8.1).
Что и требовалось.
Рассмотрим теперь специальную процедуру получения ортогональных систем, из которой можно будет получить факт существования ОНБ.
Теорема 8.3 (метод ортогонализации Грама-Шмидта).
Пусть задана линейно независимая
система
.
Тогда существует эквивалентная ей
ортогональная система
,
которая может быть получена следующим
образом:
1.
;
2.
,
,
где
.
Доказательство. Докажем
существование ортогональной системы
эквивалентной
индукцией
по числу векторов в
.
Ясно, что содержательный смысл рассуждения
по индукции в данном случае начинается
с
.
Для
имеем:
.
Здесь коэффициент
имеет смысл, ибо вектор
как вектор из линейно независимой
системы. Очевидно, что системы
и
эквивалентны. Пусть теперь теорема
справедлива для всех
.
Докажем результат для
.
Найдем скалярное произведение
,
где
.
Имеем:
.
Как видим, в итоге получается ортогональная
система. Каждый из коэффициентов
имеет смысл, ибо система
эквивалентна по индуктивному предположению
линейно независимой системе
(
)
и потому не может содержать нулевых
векторов (см. т. 5.5). Эквивалентность
систем, состоящих из
векторов, легко следует из пункта 2
теоремы.
Следствие 1. Ортонормированные базисы существуют.
Действительно, достаточно выбрать какой-либо базис в пространстве и подвергнуть его ортогонализации по схеме доказанной теоремы, а затем пронормировать получившиеся векторы.
Следствие 2. Каждую ортонормированную систему можно дополнить до ортонормированного базиса.
Пример 8.5. Построить ортонормированный
базис линейной оболочки
,
.
Скалярное произведение выберем такое
же, как в примере 8.2 для
.
Легко проверяется линейная независимость системы, на которой построена линейная оболочка. Поэтому применим метод ортогонализации к данной системе. Имеем:
;
.
Для вычисления
сначала вычислим коэффициенты
и
.
Получим
;
.
Поэтому
.
Проверка ортогональности системы
тривиальна. Подвергнем ее нормированию.
Нормирующие множители:
.
Отсюда получаем ОНБ данной линейной
оболочки:
Задача. Выяснить, что произойдет, если процесс ортогонализации применить к линейно зависимой системе.
Определение 8.9. Пусть
,
где
– евклидово пространство. Множество
называется ортогональным к множеству
,
если каждый вектор из
ортогонален каждому вектору из
.
Обозначение:
.
Очевидно, что в этом случае и
.
В основном в дальнейшем будем интересоваться случаем ортогональных подпространств.
Теорема 8.4. Для того чтобы
подпространство
было ортогонально подпространству
необходимо и достаточно, чтобы какой-либо
базис
был ортогонален какому-либо базису
.
Доказательство. Необходимость очевидна.
Достаточность. Пусть базисом
будет
,
а базисом
–
.
Эти базисы ортогональны друг другу.
Тогда любой вектор из
представится в виде
,
а любой вектор из
– в виде
.
Остается рассмотреть скалярное
произведение:
.
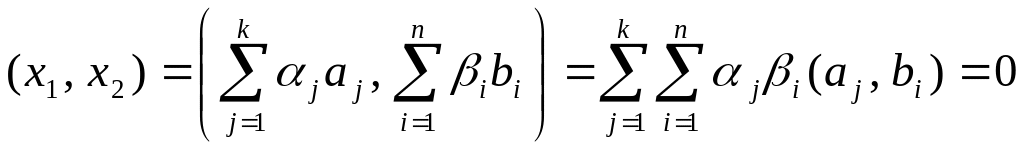Определение 8.10. Сумма подпространств
называется ортогональной, если слагаемые
в ней попарно ортогональны. Обозначение:
,
для
.
Лемма 8.2. Ортогональная сумма является прямой суммой.
Этот результат есть простое следствие второго критерия прямой суммы (см. т. 5.8).
Определение 8.11. Пусть
– евклидово пространство и
– произвольное непустое подмножество.
Тогда ортогональным дополнением к
А в Е называют множество векторов
из Е ортогональных к А. Обозначение:
.
Иными словами
.
Лемма 8.3. Ортогональное дополнение к произвольному непустому подмножеству в Е есть подпространство в Е.
Доказательство представляет собой простое упражнение на применения критерия подпространства (см. т. 5.1).
Теорема 8.5 (о разложении евклидова пространства).
Для любого полпространства
евклидова пространства Е справедливо
представление:
.
Доказательство. Пусть
будет ОНБ в
,
а
– ОН базис в
.
Покажем, что объединенная система
является базисом в Е. Объединенная
система очевидно ортонормированная.
Если она не является базисом в Е, то
она может быть дополнена до ОНБ по
следствию 2 из теоремы 8.3. Пусть одним
из дополняющих векторов будет
.
Тогда этот вектор ортогонален базису
,
и значит, ортогонален
.
Тогда
.
С другой стороны, вектор
ортогонален
базису
,
значит, ортогонален
.
Отсюда по лемме 8.1 получаем, что
.
Таким образом, дополнения до базиса
объединенной системы не существует,
т.е. она сама является ОН базисом Е.
Что доказывает теорему.
Добавим к сказанному несколько свойств ортогонального дополнения:
1.
;
2.
;
3.
;
4.
;
5.
;
подпространств.
Доказательство 3
.
Ясно, что
.
С другой стороны, из предыдущей теоремы
получаем:
.
Теперь из соображений размерности имеем
требуемое.
Доказательство 4
.
,
;
.