Определитель Вандермонда

Определение 4.19. Матрицей Вандермонда порядка называется матрица вида

,

определитель которой называется определителем Вандермонда.

Отметим красивый результат, посвященный вычислению такого специфического определителя. Именно:

Теорема 4.8. Справедлива следующая формула для вычисления определителя Вандермонда:

.

Доказательство получается индукцией по . Для формула очевидна. Делаем индуктивное предположение, что для всех , теорема справедлива. Будем ее доказывать, для случая . Изменим матрицу определителя следующим образом. Вычтем из каждой строки начиная снизу предыдущую строку, умноженную на . Получим определитель

= .

Последнее выражение получается после раскрытия преобразованного определителя по первому столбцу в соответствии с теоремой 4.5 и вынесения общих множителей по свойству 3. Теперь справа находится определитель Вандермонда порядка , и можно воспользоваться индуктивным предположением. Тогда имеем:

.

Полная линейная группа

В предыдущих построениях были описаны кольцо квадратных матриц и, в частности, аддитивная группа матриц. Возникает вопрос о построении мультипликативной группы матриц. Эта группа должна содержать квадратные матрицы одного порядка и быть заведомо неабелевой. Но на всем множестве получить групповую конструкцию не удается. В этом легко убедиться, используя теорему 4.7. Действительно, пусть определитель матрицы равен нулю. Обозначим обратный элемент к матрице через . В силу того, что единичная матрица играет роль мультипликативной единицы, то должно выполняться равенство . Но по теореме об умножении определителей 4.7 имеем:

.

Полученное противоречие говорит о том, что матрицы с нулевыми определителями заведомо не могут войти в гипотетическую мультипликативную группу.

Определение 4.20. Матрица называется невырожденной (неособенной), если ее определитель отличен от нуля. В противном случае матрица называется вырожденной (особенной).

Обозначим множество невырожденных матриц порядка над полем Р через .

Тогда справедлива следующая теорема.

Теорема 4.9. Пара – группа.

Доказательство. Алгебраичность операции следует из того, что матрицы заданы над полем. Поэтому, если , то , ибо в поле нет делителей нуля. Так что . Ассоциативность и наличие единицы уже обсуждалось в более широком контексте. Наконец, надо убедиться, что каждая матрица из рассматриваемого множества имеет в этом множестве обратный элемент. Этот обратный элемент может быть получен конструктивно. Действительно, пусть . Заменим каждый элемент матрицы его алгебраическим дополнением . Получим матрицу , затем транспонируем полученную матрицу и умножим результат на . Утверждаем, что . Ясно, что нужно проверить условие . Рассмотрим первое слева произведение и обозначим .

,

т.е. . Второе соотношение проверяется аналогично. Здесь использовали теорему 4.5 о разложении определителя по строке и теорему 4.6 о «чужих» дополнениях. Теорема доказана.

Полученная группа носит название полной линейной группы и обозначается или .

Определение 4.21. Пусть задана матрица . Тогда матрица называется обратной к матрице А, если выполнено условие

.

Теорема 4.10 (критерий обратимости матрицы)

Матрица обратима тогда и только тогда, когда она невырожденная.

Необходимость доказывается применением к указанному соотношению теоремы 4.7, а достаточность следует из теоремы 4.9.

Следствие. .

Все предыдущее в этом разделе говорит о том, что получен алгоритм вычисления обратной матрицы. Именно:

Вход: матрица .

1. Вычислить определитель матрицы А. Если то завершить работу с резолюцией «обратная матрица не существует», иначе продолжать.

2. Построить матрицу , где суть алгебраические дополнения к элементам (матрица называется присоединенной).

3. Транспонировать матрицу . Получить .

4. Вычислить .

5. Подать на выход .

Пример 4.10. Пусть требуется найти матрицу, обратную к А:

.

Вычисляем определитель: . Обратная матрица существует.

Теперь вычислим присоединенную матрицу:

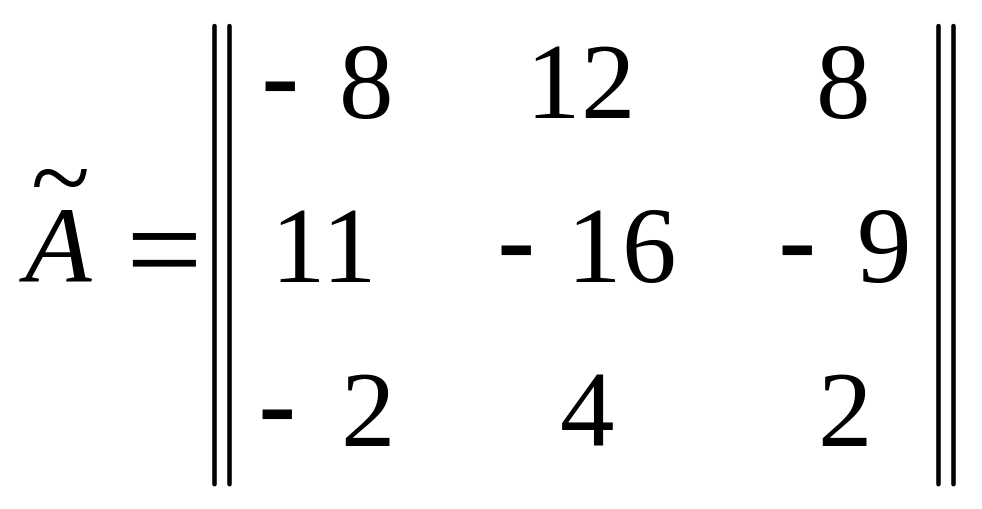и .

И, наконец,

.

Проверка легко подтверждает этот ответ.