16

IV. МАТРИЦЫ И ОПРЕДЕЛИТЕЛИ

Понятие о матрице

Понятие матрицы возникает в математике в самых разных ситуациях, но наиболее наглядно в системах линейных алгебраических уравнений (СЛАУ). Действительно, пусть задана система уравнений с неизвестными над полем Р:

,

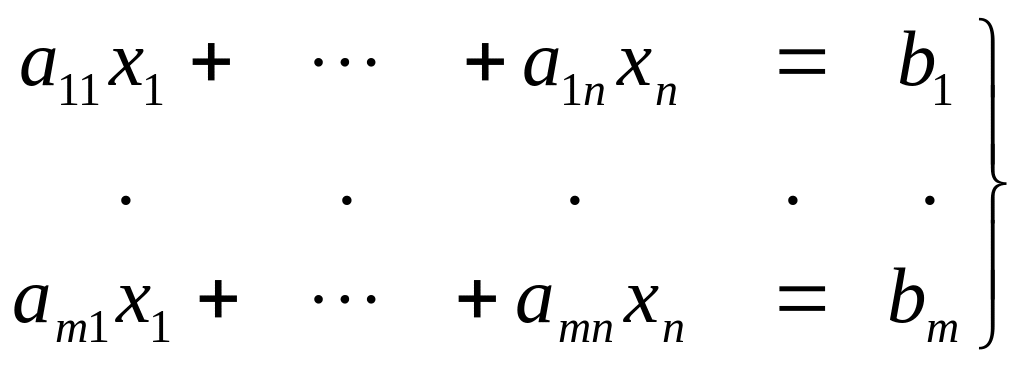где ,

Вполне естественно ожидать, что вопросы существования решения, а также само возможное решение зависит от прямоугольных таблиц вида:

, или .

Такие прямоугольные таблицы называют матрицами над полем Р. Последняя называется расширенной матрицей системы. Числа и называют размерами матрицы А. Если , то матрицу называют квадратной, а ее размер – порядком. Элементы поля называют элементами матрицы и собраны в строки и столбцы. В случае двойной индексации первый индекс означает номер строки, в которой стоит элемент, а второй – номер столбца. Строки нумеруются сверху вниз, а столбцы слева направо.

Множество матриц над полем Р размеров обозначим . А в случае – . Матрицы обычно обозначают большими латинскими буквами. Если надо указать, из каких элементов состоит матрица, то пишут

Определение 4.1. Матрица, все элементы которой равны нулю, называется нулевой.

Определение 4.2. Матрица называется верхней (нижней) треугольной, если для .

Определение 4.3. Квадратная матрица называется диагональной, если она одновременно является как нижней, так и верхней треугольной.

Определение 4.4. Совокупность элементов квадратной матрицы, расположенных вдоль диагонали, идущей из левого верхнего угла в правый нижний, называется главной диагональю матрицы, а вторая диагональ – побочной.

Определение 4.5. Диагональная матрица называется скалярной, если все диагональные ее элементы равны между собой.

Определение 4.6. Скалярная матрица называется единичной, если ее диагональные элементы равны единице поля.

Определение 4.7. Матрица вида

,

где – квадратные матрицы (блоки) произвольных порядков, расположенные так, что их главные диагонали составляют главную диагональ матрицы А, а остальные элементы, не входящие в блоки , равны нулю, называется клеточно-диагональной, или квазидиагональной.

Операции над матрицами

Определение 4.8. Две матрицы одинаковых размеров называются равными, если совпадают их элементы, стоящие на соответствующих местах.

Замечание. Для матриц равенство , т.е. означает для всех и .

Далее, рассмотрим операции над матрицами.

Определение 4.9. Пусть заданы матрицы . Их суммой называется матрица .

Таким образом, можно складывать матрицы над данным полем одинаковых размеров. При этом получается матрица тех же размеров.

Пример 4.1.

.

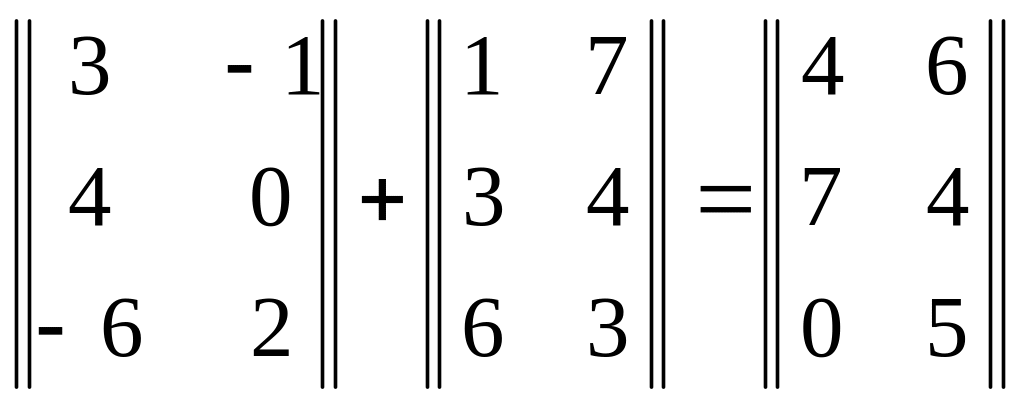Теорема 4.1. Пара – абелева группа.

Доказательство получается простой проверкой аксиом абелевой группы. Нейтральным элементом служит нулевая матрица соответствующих размеров.

Определение 4.10. Пусть задана матрица элемент поля . Тогда произведением матрицы на элемент называется матрица

.

Следовательно, умножая матрицу произвольных размеров на элемент поля, получаем матрицу тех же размеров, у которой каждый элемент есть произведение соответствующего элемента исходной матрицы на данный элемент поля.

Пример 4.2.

.

Отметим простейшие свойства операции умножения на элемент поля. Именно:

0. , ;

1. , ;

2. , ;

3. , .

Доказательство этих свойств не представляет труда.

Наконец, рассмотрим операцию умножения матриц.

Определение 4.11. Пусть заданы матрицы и . Произведением матрицы А на матрицу В называется матрица , такая, что для всех и .

Как видим из определения, не любые две матрицы можно перемножить. Требуется, чтобы число столбцов матрицы слева совпадало с количеством строк матрицы справа. Но даже если существуют оба произведения и , то как легко заметить на примерах, произведение вообще говоря не равно произведению . Это легко объясняется несимметричностью использования строк и столбцов левого и правого сомножителей.

Пример 4.3.

.

Уже отмечалось, умножение матриц не коммутативно. Тем не менее, эта операция обладает свойством ассоциативности.

Лемма 4.1. Умножение матриц ассоциативно.

Теорема 4.2. – ассоциативное кольцо с единицей. Если , то кольцо имеет делители нуля.

Доказательство сводится к проверке аксиом кольца. При этом можно учесть теорему 4.1. В качестве единицы выступает единичная матрица . Действительно, эту матрицу можно представить в виде , где Поэтому, например, если

, то .

Отметим еще важное свойство, связывающее операцию умножения матрицы на элемент поля и умножение собственно матриц. Именно:

.

Определение 4.12. Пусть задана матрица . Тогда матрица называется транспонированной по отношению к А.

Транспонирование означает, что строки матрицы А становятся столбцами матрицы в соответствии с нумерацией. Отметим свойства операции транспонирования:

0. ;

1. ;

2. ;

3. ;

4. .