Изоморфизм линейных пространств
При изучении алгебраических структур легко заметить известны параллелизм свойств, связанных с операциями. Это касается и линейных пространств. Для наведения определенного порядка в бесконечной совокупности пространств изобретен специальный инструмент. Его называют изоморфизмом ЛП.
Определение 5.19. Пусть заданы
два линейных пространства над одним и
тем же полем
и
.
Изоморфизмом из
в
называется биекция
,
сохраняющая линейные операции, т.е.,
1.
;
2.
.
Обозначение:
.
Лемма 5.17. Бинарное отношение изоморфизма линейных пространств является отношением эквивалентности на множестве всех линейных пространств над данным полем.
Приведем еще несколько важных свойств изоморфизма .
1.
;
2.
;
3.
;
4. Линейно зависимая система из отображается в линейно зависимую в ;
5. Линейно независимая система из отображается в линейно независимую в ;
6. Базис отображается в базис ;
7.
;
8. Прямая сумма подпространств в отображается в прямую сумму образов этих подпространств в .
Докажем последнее свойство. Во-первых,
покажем, что образ подпространства
является подпространством. Действительно,
воспользуемся критерием подпространства
(см. теорему 5.1) . Пусть
– некоторое произвольное подпространство
в
,
а
,
т.е., совокупность образов элементов из
в
.
Тогда
.
Последнее включение следует из того,
что линейная комбинация
,
ибо
– подпространство в
.
Здесь учли еще, что
и
для
.
Рассмотрим для простоты случай двух
слагаемых в прямой сумме. Пусть имеется
прямая сумма
в
.
Образами этих подпространств в
пусть будут
и
.
Составим из последних сумму
.
Предположим, что слагаемые в ней имеют
общий ненулевой вектор
.
Тогда прообраз этого вектора
будет лежать как в
,
так и
,
т.е., находиться в пересечении
.
При этом
,
ибо у нулевого вектора в
образом служит лишь нулевой вектор из
(см. свойство изоморфизма 1
).
А это противоречит следствию 2 из теоремы
5.8. Свойство доказано.
Отметим теперь эквивалентное определению 5.19 утверждение.
Теорема 5.9 (критерий изоморфности пространств).
Два конечномерных линейных пространства, заданных над одним и тем же полем, изоморфны тогда и только тогда, когда имеют одинаковые размерности.
Доказательство. Необходимость. Следует из свойства 7 изоморфизма.
Достаточность. Пусть два линейных
пространства
и
заданы над полем Р и
.
Зададим в
базис
,
а в
– базис
и определим отображение
равенством:
,
,
положим
.
Легко видеть, что так определенное
отображение является биективным и
сохраняет линейные операции. Именно
.
А также
.
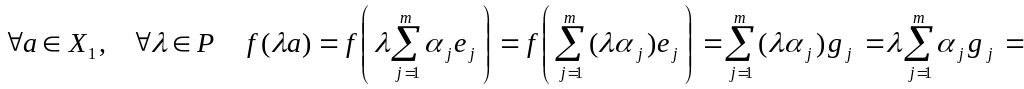
Здесь приняли, что
,
.
Таким образом, теорема полностью доказана.
В итоге все конечномерные пространства, заданные над одним общим полем, можно разбить на попарно непересекающиеся классы изоморфных между собой пространств (лемма 5.17). Эти пространства с точки зрения свойств операций в них неразличимы. Хотя, конечно, конкретная природа элементов этих пространств может существенным образом отличаться.
Пример 5.18. В соответствии с последней теоремой изоморфны пространства
1)
и
;
2)
.
Последний пример требует разъяснения.
Рассмотрим пространство
-мерных
строк над полем Р. В этом пространстве
довольно легко обнаружить базис,
состоящий из т.н. единичных строк:
. . . . . . . . . .
По второму критерию линейной зависимости
эта система линейно независима
(рассуждение от противного). И очевидно,
что каждый вектор из
линейно через такую системы выражается:
.
Таким образом,
.
Такие пространства (в том числе и
пространства столбцов высоты
)
будем называть арифметическими и
обозначать
.
Учитывая, что
,
любые вычисления в
-мерном
пространстве над полем Р можно
производить, совершив изоморфный
переход, в арифметическом пространстве.
Эти пространства оказываются удачной
моделью любого пространства соответствующей
размерности в том, что касается линейных
операций.