Эквивалентные системы векторов

Определение 5.8. Две системы векторов называются эквивалентными, если каждая из них линейно выражается через другую систему.

Лемма 5.4 (критерий эквивалентности).

Две системы векторов линейного пространства эквивалентны тогда и только тогда, когда совпадают их линейные оболочки.

Лемма 5.5. Бинарное отношение эквивалентности систем векторов является отношением эквивалентности, т.е. рефлексивно, симметрично и транзитивно.

Из последней леммы следует, что все системы векторов данного пространства можно разбить на попарно непересекающиеся классы эквивалентности. Каждому такому классу будет отвечать некоторая линейная оболочка.

Теорема 5.5 (сравнения).

Пусть заданы две системы векторов: и , причем первая – линейно независимая. Тогда, если каждый вектор линейно выражается через

векторы , то .

Доказательство. Построим новую систему . Эта система линейно зависима, ибо первый вектор линейно выражается через остальные. Применим к этой системе теорему 5.4. Так как , как вектор из ЛНЗ системы, то найдется вектор , , такой, что линейно выражается через предыдущие. Поэтому в линейных представлениях векторов системы он может быть заменен соответствующими линейными комбинациями. Если вектор удалить из системы , то получим систему , через которую выражается система . Добавим слева в вектор и получим систему , которая, очевидно, является ЛЗ. И согласно второму критерию ЛЗ в ней должен быть вектор, выражающийся через предыдущие. Но этим не может быть вектор , так как принадлежит ЛНЗ системе, и по той же причине. Поэтому найдется вектор , который выражается через предыдущие. Если его удалить из системы , то получим систему , через которую выражается . Присоединим к вектор слева и т.д. В этой процедуре важно то, что после удаления вектора системы получается система, через которую линейно выражается система . При этом векторы не могут исчерпаться ранее того, как будут присоединены все векторы из . Что и означает .

Следствие 1. Эквивалентные линейно независимые системы содержат одинаковое количество векторов.

Следствие 2. Каждая система из более векторов взятая из линейной оболочки, построенной на векторах, линейно зависима.

Определение 5.9. Базой ненулевой системы векторов называется эквивалентная ей подсистема.

Замечание. Нулевая система базы не имеет.

Рассмотрим некоторые свойства базы.

1. База ЛНЗ системы совпадает с самой системой.

2. Подсистема ненулевой системы будет ее базой тогда и только тогда, когда она максимально ЛНЗ.

Замечание. Максимально ЛНЗ подсистема та, к которой нельзя присоединить ни одного вектора системы, сохраняя свойство ЛНЗ.

3. База системы не изменится, если к системе добавить вектор, являющийся линейной комбинацией векторов системы.

4. Каждый вектор системы линейно выражается через векторы базы единственным образом.

Доказательство последнего свойства можно вывести из того факта, что если вектор выражается через ЛНЗ систему, то это его представление единственно. Действительно, пусть вектор линейно выражается через ЛНЗ систему двумя способами.

.

Тогда ,

И по критерию ЛНЗ получаем, что , т.е. .

Однозначное описание вектора линейной оболочки через базу порождающей системы можно осуществить, отображая сам вектор в строку коэффициентов, которую удобно назвать координатной строкой вектора в данной базе: если , то

.

Такое отображение, очевидно, обладает линейными свойствами, т.е., линейные операции над векторами отвечают такие же операции над координатными строками.

Учитывая следствие 1 предыдущей теоремы, можно утверждать, что две базы одной и той же системы эквивалентны. Отсюда получаем новое определение.

Определение 5.10. Рангом ненулевой системы векторов называется число векторов какой-либо его базы. Ранг нулевой системы считается равным нулю.

Рассмотрим теперь некоторые свойства ранга системы.

1. Ранг ЛНЗ системы равен числу векторов системы.

2. Ранг ЛЗ системы меньше числа векторов системы.

3. Ранги эквивалентных систем равны.

4. Ранг подсистемы не превосходит ранга системы.

5. Если ранг подсистемы равен рангу системы, то у них есть общая база.

6. Если система линейно выражается через систему , то ранг не превосходит ранга .

7. Ранг системы не изменится, если к ней присоединить или удалить из нее вектор, являющийся линейной комбинацией остальных.

Рассмотрим теперь, т.н., элементарные преобразования системы векторов.

Определение 5.11. Элементарными преобразованиями (ЭП) системы векторов называют следующие:

1. Перемена местами (транспозиция) двух векторов системы;

2. Умножение любого вектора системы на элемент поля ;

3. Прибавление к любому вектору любого другого вектора системы, умноженного на произвольный элемент поля.

Лемма 5.6. Элементарные преобразования системы векторов являются эквивалентными, т.е., приводят к системе эквивалентной данной.

Посмотрим теперь, как можно вычислять базу и ранг системы, пользуясь элементарными преобразованиями. Это удобно сделать на примере работы с матрицами-строками, ибо, как было сказано, векторы легко описывать в координатной форме.

Пример 5.10. Пусть задана система векторов

.

Найдем какую-либо ее базу и определим ранг. Для этого приведем ее элементарными, а значит эквивалентными, преобразованиями к треугольному (трапецеидальному) виду. Получим

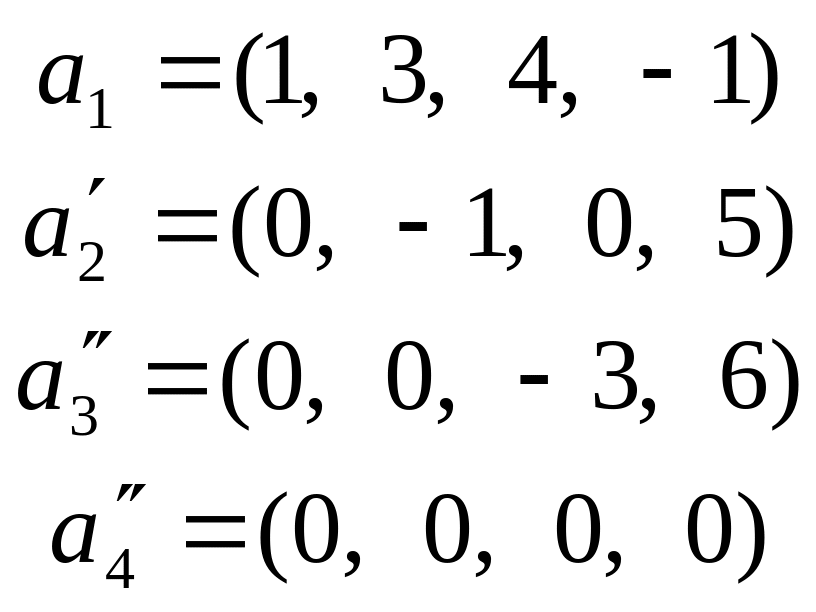
Ясно, что последняя система эквивалентна исходной. Нулевой вектор не может входить в базу и поэтому его естественно удалить. После чего остается три вектора, образующие ЛНЗ систему, ибо ни один из них не может быть выражен через нижестоящие, а первый вектор не равен нулю (см. теорему 5.4). Поэтому ранг последней системы, а значит и первой, равен трем. Так как векторы не переставлялись местами и сохранили свои номера, то первые три вектора исходной системы образуют одну из ее баз.