
Колебания маятника под действием сил сухого трения
Пусть в произвольный момент времени штангу, на которой закреплены только элемент сухого трения и груз, отклонили от положения равновесия на угол φ, как показано на рис. 4.
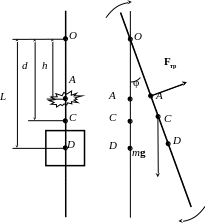
Рис. 4. Схема маятника, колеблющегося под действием силы тяжести и силы сухого трения
Под действием силы тяжести маятник стремится вернуться в первоначальное положение. Сила трения Fтр, модуль которой не зависит от угла φ отклонения маятника, направлена против движения кисточки, закреплённой на штанге в т. A. Основной закон динамики вращательного движения в этом случае записывается так:
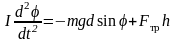 .
(19)
.
(19)
Из (19) после элементарных преобразований получим линейное неоднородное дифференциальное уравнение второго порядка:
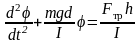 .
(20)
.
(20)
Поскольку
|Fтр| = const, то циклическая
частота ω затухающих колебаний
величины φ совпадает с циклической
частотой 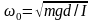 свободных колебаний той же системы в
отсутствие трения [3, с. 118-119].
свободных колебаний той же системы в
отсутствие трения [3, с. 118-119].
Чтобы оценить значение силы трения, воспользуемся законом сохранения энергии, в соответствии с которым работа силы трения Aтр за половину периода T/2 равна убыли механической энергии маятника за тот же промежуток времени. Пусть маятник отклонили от положения равновесия на угол φ1, как показано на рис. 5.
|
|
Рис. 5. Изменение положения маятника через половину периода колебаний |
Рис. 6. Временнáя зависимость амплитуды колебаний, затухающих под действием сил сухого трения |
В начальный момент времени маятник отпустили без сообщения дополнительной скорости (Ek1 = 0). Если в качестве нулевого уровня потенциальной энергии выбрать уровень, проходящий через центр масс маятника в положении равновесия, то в начальный момент времени энергия маятника равна
E1 = Ep1 = mg|ОС|·(1 – cos φ1) = mgd(1 – cos φ1) ≈ mgd φ12 / 2. (21)
При получении (21) учтено, что угол φ1 малый, и поэтому sin φ1 ≈ φ1.
Если момент сил трения не слишком большой, то через время T/2 маятник отклонится с другой стороны от положения равновесия на максимальный угол φ2 < φ1 (Ek2 = 0). При этом элемент сухого трения пройдёт расстояние, равное длине дуги |ОА|·(φ1+φ2) = h (φ1+φ2), и сила трения совершит работу
Aтр = Fтр h (φ1+φ2), (22)
тогда механическая энергия маятника уменьшится до значения
E2 = Ep2 = mgd(1 – cos φ2) ≈ mgd φ22 / 2. (23)
Таким образом, из закона сохранения энергии Aтр = E1 – E2 следует
Fтр h (φ1+φ2) ≈ mgd ( φ12 – φ22) / 2, (24)
откуда путём элементарных математических преобразований получим
Fтр ≈ mgd (φ1 – φ2) / (2h) = mgd Δφ1/2 / (2h), (25)
где Δφ1/2 – угол, на который уменьшается амплитуда колебаний маятника за половину периода T/2. За полный период амплитуда колебаний уменьшится на Δφ = 2Δφ1/2, тогда выражение (25) можно записать в виде:
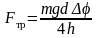 . (26)
. (26)
Поскольку подобные рассуждения можно произвести и для первого, и для второго, и для последующих периодов колебания маятника, то последовательность максимальных отклонений образует убывающую арифметическую прогрессию (линейная зависимость от времени), и колебания полностью прекращаются через конечное число циклов. В противоположность этому, если затухание колебаний происходит из-за вязкого трения, то максимальные отклонения убывают в геометрической прогрессии (экспоненциально) и формально движение продолжается бесконечно долго. График колебаний, затухающих под действием сил сухого трения, представлен на рис. 6, где пунктирная линия изображает зависимость амплитуды от времени.

 а
а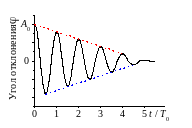 б
б