
Лабораторная работа № 11. Моделирование механических затухающих колебаний
Цель работы: изучение затухающих колебаний методом моделирования. Наблюдение затухающих электромагнитных колебаний, изучение их характеристик.
Краткая теория
Экспериментальное изучение механических колебаний, в том числе затухающих, является трудоемкой задачей, требующей высокой точности постановки эксперимента. В условиях учебной лаборатории весьма перспективным является использование методов моделирования. При помощи моделирования наглядные и достаточно точные количественные характеристики затухающих механических колебаний могут быть получены значительно проще.
Условимся называть моделированием процесс замены изучения какого-либо явления в реальных условиях изучением его при помощи тех или иных моделей, в условиях, специально подобранных для удобства экспериментирования. При этом, кроме измерения размеров тел, участвующих в явлении, и материалов, из которых они изготовлены, очень часто исследуемый процесс может быть заменен другим, который либо зависит от наиболее важных для данного явления величин, либо имеет совсем другую природу, но сходное математическое описание. Моделирование является продолжением эксперимента новыми средствами.
Данная
лабораторная работа посвящена физическому
и математическому моделированию,
основанному на математических аналогиях
между механическими колебаниями и
электрическими колебаниями в
 - цепях. Физической моделью для изучения
характеристик затухающих колебаний
является колебательный контур, в котором
периодически возбуждаются колебания.
- цепях. Физической моделью для изучения
характеристик затухающих колебаний
является колебательный контур, в котором
периодически возбуждаются колебания.
Механические колебания
Колебательными
называются процессы, при которых
параметры, характеризующие состояние
колебательной системы, обладают
определенной повторяемостью во времени.
Такими процессами, например, являются
суточные и годовые колебания температуры
поверхности Земли, колебания маятников
и т. п. Если промежутки времени, через
которые состояния системы повторяется,
равны между собой, то колебания называются
периодическими, а промежуток времени
между двумя последовательными одинаковыми
состояниями системы – периодом колебаний
 .
Среди периодических колебаний особое
место занимают колебания гармонические,
т. е. колебания, при которых характеристики
движения системы изменяются по
гармоническому закону, например:
.
Среди периодических колебаний особое
место занимают колебания гармонические,
т. е. колебания, при которых характеристики
движения системы изменяются по
гармоническому закону, например:
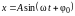 , (1)
, (1)
где
 - отклонение материальной точки от
положения равновесия (смещение);
- отклонение материальной точки от
положения равновесия (смещение);
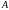 – амплитуда колебаний (максимальное
отклонение от положения равновесия);
– амплитуда колебаний (максимальное
отклонение от положения равновесия);
 - фаза колебаний;
- фаза колебаний;
 - начальная фаза (значение фазы для
колебаний в момент времени
- начальная фаза (значение фазы для
колебаний в момент времени
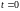 );
);
 - круговая или циклическая частота
колебаний.
- круговая или циклическая частота
колебаний.
а) Свободные колебания при отсутствии трения (собственные колебания)
Свободными
называются колебания системы, выведенной
из положения равновесия и представленной
затем самой себе. Предположим, что на
тело, выведенное из положения равновесия,
действуют силы, пропорциональные
смещению и противоположно ему направленные:
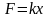 ,
где
,
где
 - коэффициент пропорциональности. Силы,
изменяющиеся подобным образом, как
упругие силы, независимо от их природы
называются «квазиупругими». Если
пренебречь силами трения, уравнение
движения по второму закону Ньютона
можно записать в виде
- коэффициент пропорциональности. Силы,
изменяющиеся подобным образом, как
упругие силы, независимо от их природы
называются «квазиупругими». Если
пренебречь силами трения, уравнение
движения по второму закону Ньютона
можно записать в виде
 (2)
(2)
или
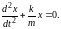 (3)
(3)
Последнее уравнение является дифференциальным уравнением гармонических колебаний, решением которого будет гармоническая функция
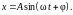 (4)
(4)
В том, что (4) действительно является решение уравнения (3) , легко убедиться путем подстановки (4) в (2):
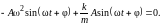 (5)
(5)
Очевидно,
что (5) будет выполняться для любого
произвольного момента времени в том
случае, если
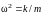 .
Следовательно, решением уравнения (3)
действительно является гармоническая
функция (4) с циклической частотой:
.
Следовательно, решением уравнения (3)
действительно является гармоническая
функция (4) с циклической частотой:
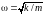 (6)
(6)
б) Свободные колебания при наличии трения (затухающие колебания)
Предположим
теперь, что на колеблющееся тело действуют
силы сопротивления движению, пропорциональны
скорости тел и противоположно направленные,
например, силы вязкого трения при малых
скоростях движения тела:
 .
.
Дифференциальное уравнение движения с учетом квазиупругих сил можно записать в виде:
 (7)
(7)
Введем
обозначения:
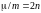 и
и
 .
С учетом этих обозначений дифференциальное
уравнение движения принимает форму:
.
С учетом этих обозначений дифференциальное
уравнение движения принимает форму:
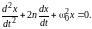 (8)
(8)
Наличие квазиупругих сил позволяет сделать заключение о том, что тело будет совершать колебательное движение. Но, в отличие от собственных колебаний, энергия колебаний будет уменьшаться, расходуясь на преодоление трения. Следовательно, амплитуда колебаний должна зависеть от времени, постоянно уменьшаясь. Кроме того, силы трения тормозят движение, что должно приводить к уменьшению частоты колебаний. С учетом сказанного решение уравнения (8) можно искать в виде:
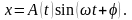 (9)
(9)
При таком законе движения частота колебаний:
 . (10)
. (10)
Решением данного уравнения является зависимость:
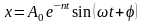 . (11)
. (11)
Это так называемые затухающие колебания. При затухающих колебаниях амплитуда с течением времени убывает по экспоненциальному закону. В то же время отношение двух последовательных амплитуд, отстоящих друг от друга на один период колебаний, от времени не зависит и остается постоянным:
 (12)
(12)
Величина
 ,
определяющая быстроту убывания амплитуды,
называется показателем затухания.
Натуральный логарифм отношения амплитуд
(12) называется логарифмическим декрементом
затухания.
,
определяющая быстроту убывания амплитуды,
называется показателем затухания.
Натуральный логарифм отношения амплитуд
(12) называется логарифмическим декрементом
затухания.
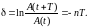 (13)
(13)
Для
практических расчетов берут обычно
абсолютное значение логарифмического
декремента:
 .
.
Как
видно из (23), показатель затухания
имеет размерность
[с-1],
т.е.
его можно записать в виде
 ,
а логарифмический декремент тогда
равен:
,
а логарифмический декремент тогда
равен:
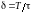 .
Величина, обратная логарифмическому
декременту затухания
.
Величина, обратная логарифмическому
декременту затухания
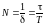 ,
показывает, какое число полных колебаний
совершит тело, пока амплитуда его
колебаний уменьшится в
,
показывает, какое число полных колебаний
совершит тело, пока амплитуда его
колебаний уменьшится в
 раз. Действительно, через
раз. Действительно, через
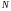 периодов после начала колебаний, т. е.
к моменту времени
периодов после начала колебаний, т. е.
к моменту времени
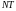 амплитуда уменьшится в
амплитуда уменьшится в
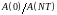 раз:
раз:
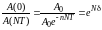
Если
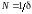 ,
амплитуда уменьшается в
раз.
,
амплитуда уменьшается в
раз.
Как это следует из (20), круговая частота колебаний равна:
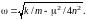 (14)
(14)
В
зависимости от величины затухания
(коэффициента трения
 )
возможны различные типы движения.
)
возможны различные типы движения.
В случае сильного затухания
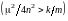 колебательное движение отсутствует.
Тело, выведенное из положения равновесия,
лишь постепенно возвращается в это
положение. Такое движение обычно
называют апериодическими колебаниями.
колебательное движение отсутствует.
Тело, выведенное из положения равновесия,
лишь постепенно возвращается в это
положение. Такое движение обычно
называют апериодическими колебаниями.В случае критического затухания
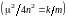 ,
т.е.
,
т.е.
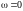 .
.Если
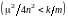 ,
т.е. в случае слабого затухания, имеют
место затухающие колебания.
,
т.е. в случае слабого затухания, имеют
место затухающие колебания.
