Лабораторная работа № 6 приложение основного закона динамики к вращательному движению.

Приборы и принадлежности: маятник Обербека, секундомер, штангенциркуль, набор грузов по 100-200 г., вертикальный масштаб.

Введение:

При вращении твердого тела вокруг неподвижной оси все частицы тела совершают вращательное движение, причем линейные скорости и ускорения различных частиц тела, вообще говоря, различны. Если угловая скорость изменяется во времени, то это изменение можно характеризовать угловым ускорением.

Для данного вращающегося тела угловое ускорение определяется действием суммы моментов сил. Такая зависимость должна существовать потому, что равновесие тела определяется равенством нулю моментов сил. Как только момент сил относительно оси вращения не будет равен нулю, равновесие нарушится, начнется вращательное движение и возникает угловое ускорение.

Для отыскания связи между угловым ускорением тела и моментом сил, действующих на него, рассмотрим движение одной какой-то выделенной частицы вращающегося тела (рис. 1). Пусть частица массой , находиться на расстоянии от оси вращения OO’.

Рис. 1

На частицу могут действовать как внутренние, так и внешние силы. Внешние силы приложены со стороны других тел, а внутренние – со стороны других частиц того же тела. Обозначим через величину проекции суммы внутренних сил, действующих на , на направление, перпендикулярное к ; – проекция на то же направление суммы внешних сил.

К каждой точке вращающегося тела применим 2-й закон Ньютона:

(1)

где - линейное ускорение точки, связанное с угловым ускорением вращающегося тела соотношением .

Подставляя в (1) значение , затем, умножая справа и слева уравнение (1) на , получим:

(1')

Величина численно равная произведению массы частицы на квадрат расстояния до оси вращения, называется моментом инерции точки относительно неподвижной оси вращения. Величины и определяют моменты внутренних и внешних сил, действующих на i-ю точку. Уравнения типа (1) и (1’) можно записать для любых точек тела. Суммируя выражение (1’) по всем элементам тела, получим:

(2)

Угловое ускорение постоянно для всех элементов, поэтому его можно вынести за знак суммы.

Величина равная сумме моментов инерции отдельных элементов, называется моментом инерции тела относительно оси вращения. Величина равна 0, так как каждая внутренняя сила имеет равную и противоположную ей силу, приложенную к другой частице тела с тем же самым плечом. Величина определяет полный момент всех сил, приложенных к телу. Вводя обозначение момента инерции тела и момента сил 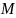, перепишем уравнение (2) в виде:

(3)

Это есть основной закон динамики твердого тела, вращающегося вокруг неподвижной оси. Этот закон аналогичен основному закону динамики поступательного движения, но вместо величины силы в уравнение (3) входит момент сил относительно оси, вместо линейного ускорения – угловое ускорение, вместо массы – момент инерции тела относительно оси вращения. Основной закон вращательного движения в форме уравнения (3) применим для таких вращающихся систем, у которых момент инерции в процессе вращения остается постоянным.

Если при вращении тела момент инерции изменяется, то применяются более общая форма основного закона вращения тела – закон изменения момента количества движения:

(4)

Величина называется импульсом моментом сил, а величина моментом количества движения.

Согласно равенству (4), изменение момента количества движения твердого тела численно равно импульсу момента приложенных к нему сил.

При отсутствии момента сил момент количества движения остается постоянным. Это следствие известно под названием закона сохранения момента количества движения.