
Примеры решения задач
Задача 1
Два
шарика с одинаковыми радиусами, массы
которых
![]() и
и
![]() ,
соединены легкой пружинкой длины
,
соединены легкой пружинкой длины
![]() и жесткостью
и жесткостью
![]() Система находится на абсолютно гладком
столе. В некоторый момент времени
пружинку растянули на
Система находится на абсолютно гладком
столе. В некоторый момент времени
пружинку растянули на
![]() и отпустили. Найти:
и отпустили. Найти:
а) период малых колебаний;
б) закон изменения во времени расстояния между шариками.
Решение.
В
начальный момент времени
![]() пружинка растянута на
и шарики относительно стола покоятся.
Поместим начало координат в центр
инерции системы, а ось OX направим
вдоль пружины. После того как шарики
будут отпущены, они начнут колебаться.
Центр инерции остается в покое, так как
полный импульс шариков в условиях задачи
сохраняется.
пружинка растянута на
и шарики относительно стола покоятся.
Поместим начало координат в центр
инерции системы, а ось OX направим
вдоль пружины. После того как шарики
будут отпущены, они начнут колебаться.
Центр инерции остается в покое, так как
полный импульс шариков в условиях задачи
сохраняется.
Введем вектор, описывающий относительное движение шариков:
![]() . (6.2)
. (6.2)
Тогда
в равновесном положении
![]() .
.
Предположив, что пружина растянута в пределах упругих деформаций, можно записать, что действующая на первый шарик упругая сила
![]()
где
![]() . (6.3)
. (6.3)
Тогда уравнение движения шариков запишутся в виде
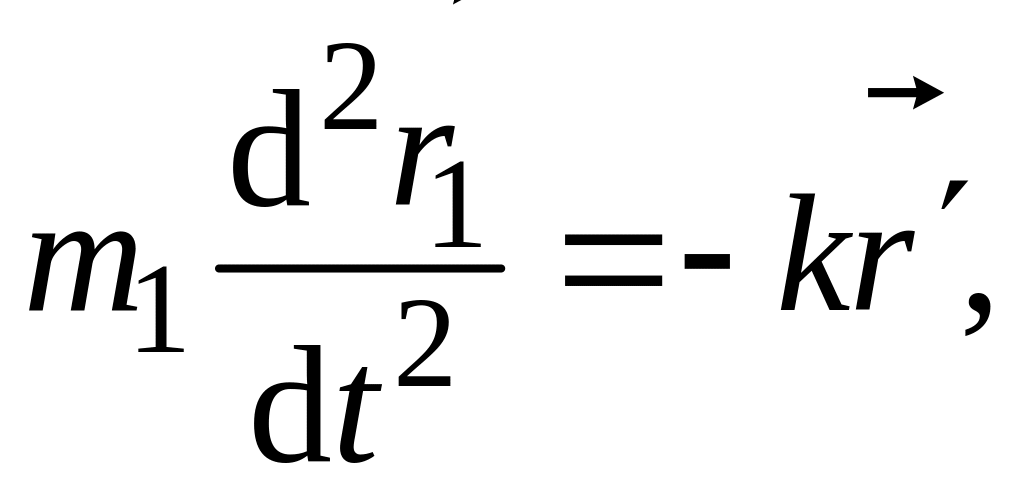 (6.4)
(6.4)
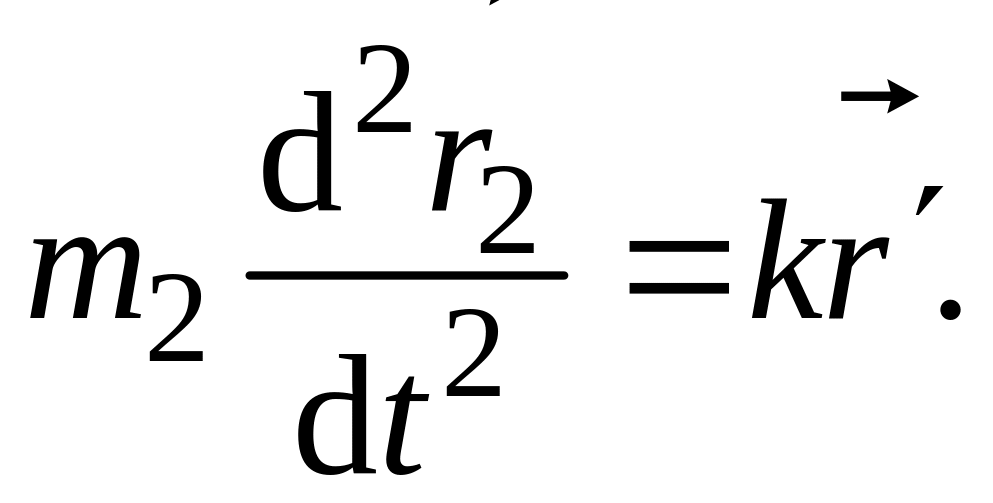 (6.5)
(6.5)
Поскольку масса пружины пренебрежимо мала, то в соответствии с выбором начала координат
![]()
Используя эту формулу, из выражения (6.2) получаем
![]()
![]() (6.6)
(6.6)
Подставив
выражения для
![]() и
и
![]() в уравнение (6.4) или (6.5), имеем
в уравнение (6.4) или (6.5), имеем
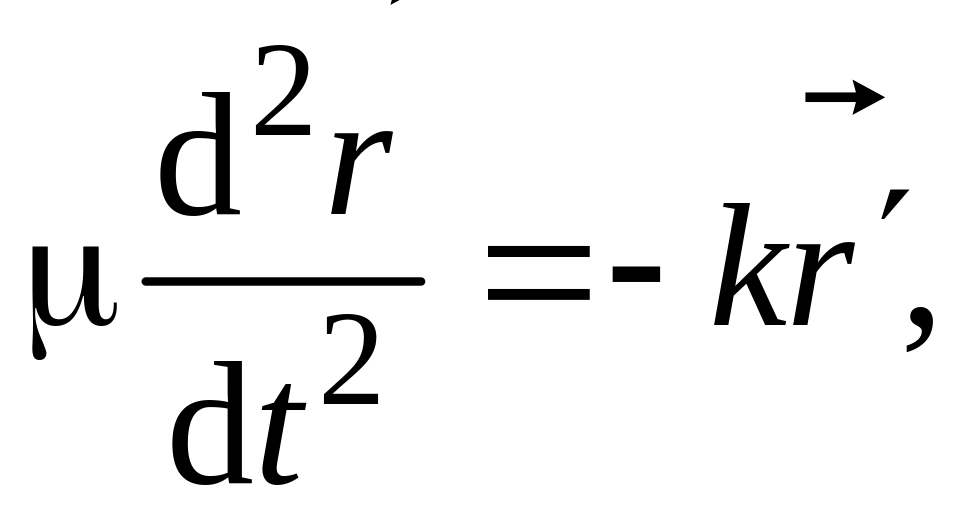 где
– приведенная
масса системы:
где
– приведенная
масса системы:
![]() .
Учитывая, что
.
Учитывая, что
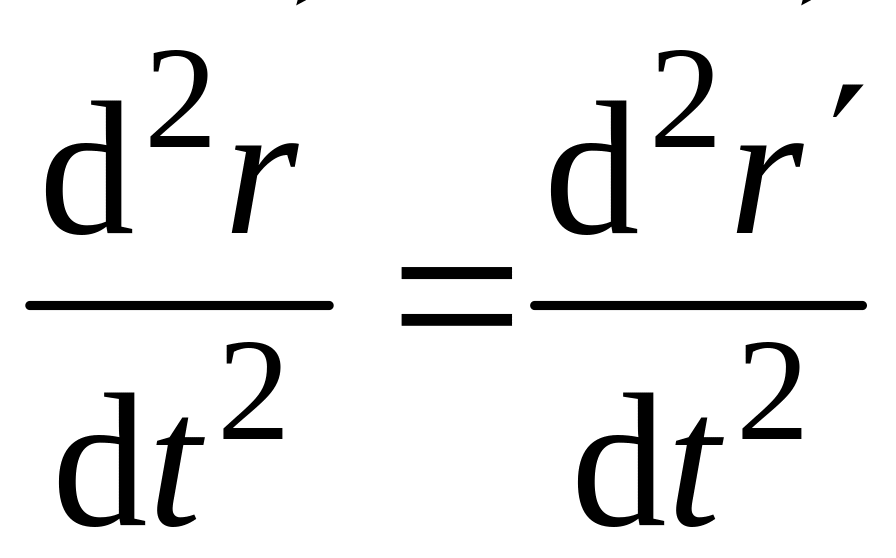 ,
приходим к уравнению гармонических
колебаний
,
приходим к уравнению гармонических
колебаний
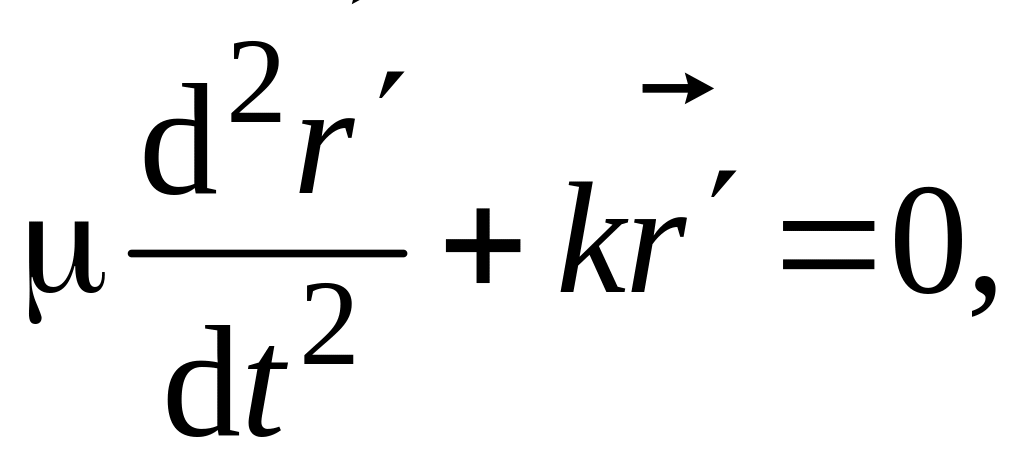
или в проекции на ось OX
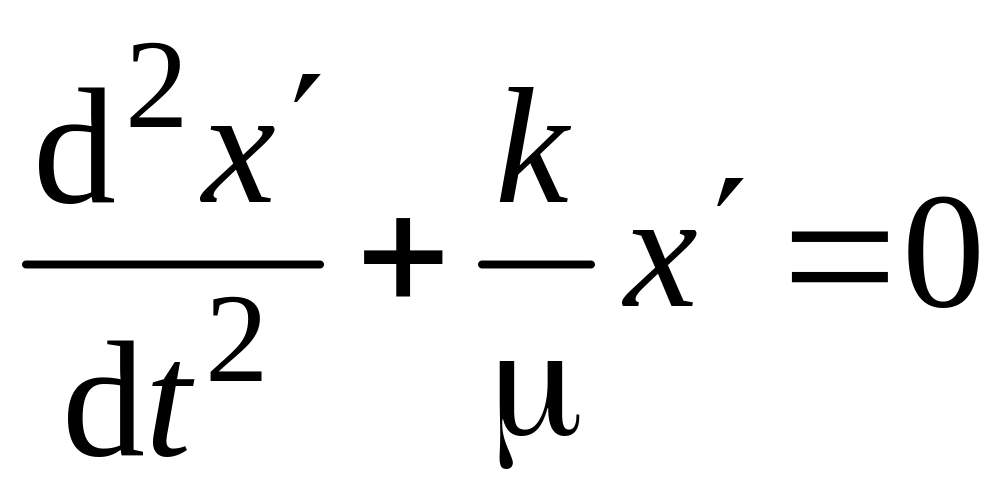 , (6.7)
, (6.7)
где
![]() .
.
Колебания шариков имеют период
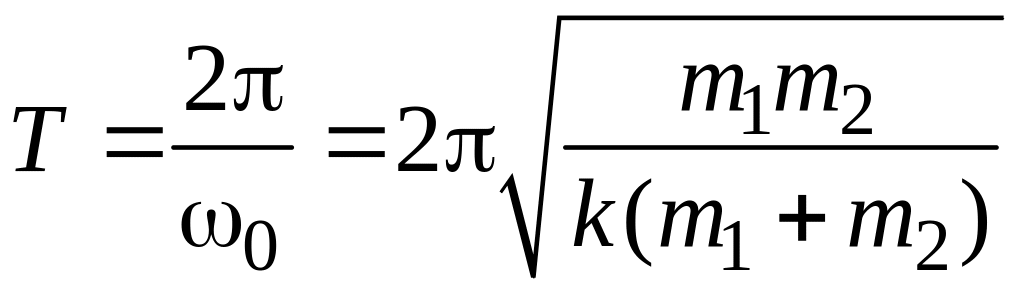 .
.
Общее решение уравнения (6.7) можно представить в виде
![]() ,
,
где
![]() и
– константы, определяемые из начальных
условий
и
– константы, определяемые из начальных
условий
![]()
![]()
Получаем уравнения
![]()
![]()
Не
ограничивая общности, можно взять
![]() .
Тогда
.
Тогда
![]() и,
и,
следовательно,
![]()
Закон
изменения относительного расстояния
![]() находится из соотношения (6.3):
находится из соотношения (6.3):
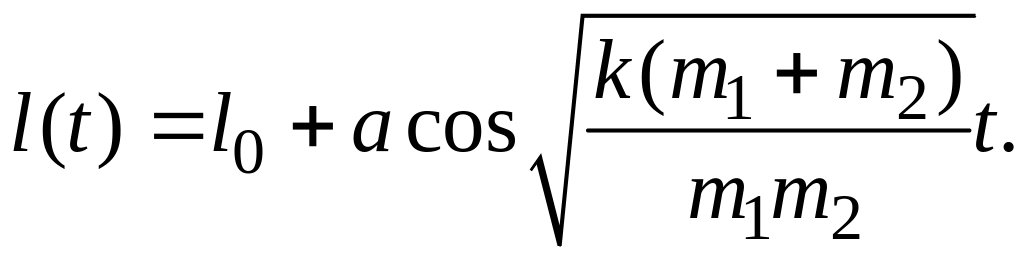
Ответ:
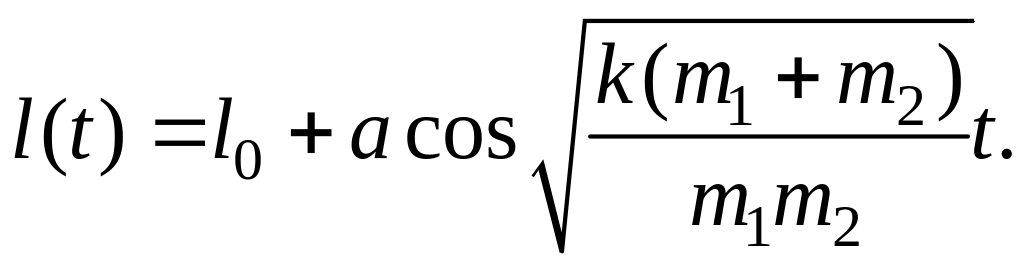
Задача 2
В
плоскости
![]() движется точка массой
под действием притягивающей к началу
координат силы, пропорциональной
расстоянию точки от начала координат.
Коэффициент пропорциональности
движется точка массой
под действием притягивающей к началу
координат силы, пропорциональной
расстоянию точки от начала координат.
Коэффициент пропорциональности
![]() .
В начальный момент
положение точки определяется вектором
.
В начальный момент
положение точки определяется вектором
![]() и ее начальная скорость
и ее начальная скорость
![]() .
Найти уравнение траектории точки.
.
Найти уравнение траектории точки.
Решение.
Уравнение движения точки:
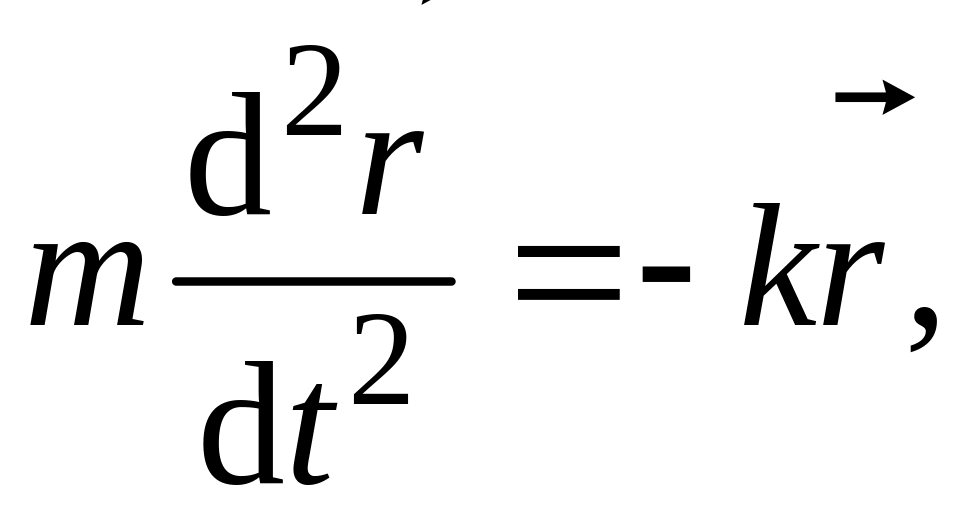 ,
,
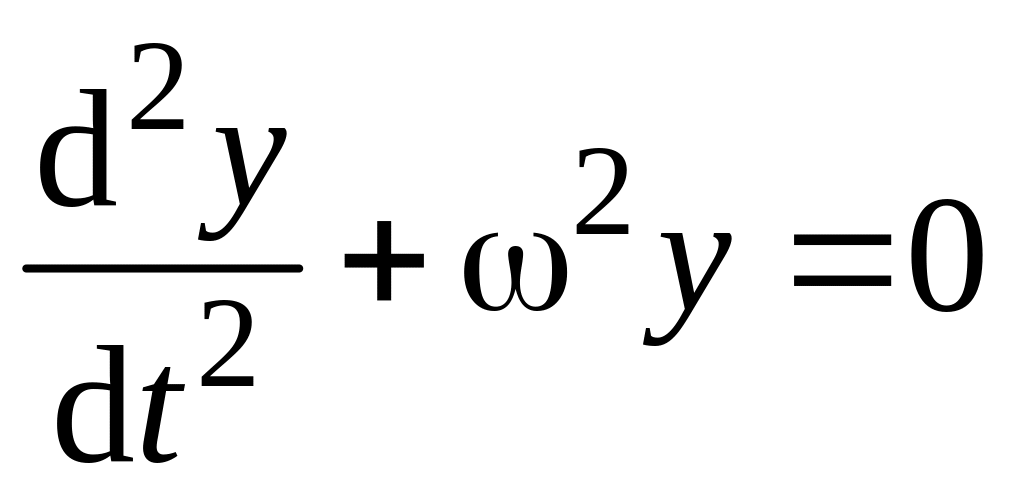 ,
,
![]()
Характеристическое
уравнение последних соотношений имеет
вид
![]() ,
его корни мнимые, поэтому общее решение
дифференциальных уравнений движения
таково:
,
его корни мнимые, поэтому общее решение
дифференциальных уравнений движения
таково:
![]()
![]()
Вместо
постоянных интегрирования
![]() введем новые постоянные
введем новые постоянные
![]() так что
так что
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
Тогда общее решение дифференциальных
уравнений движения таково:
.
Тогда общее решение дифференциальных
уравнений движения таково:
![]() ,
,
![]()
Найдем производные по времени этих равенств:
![]() ,
,
![]() .
.
Определим произвольные постоянные, подставляя начальные условия в последние четыре уравнения. Получаем систему уравнений:
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
Отсюда
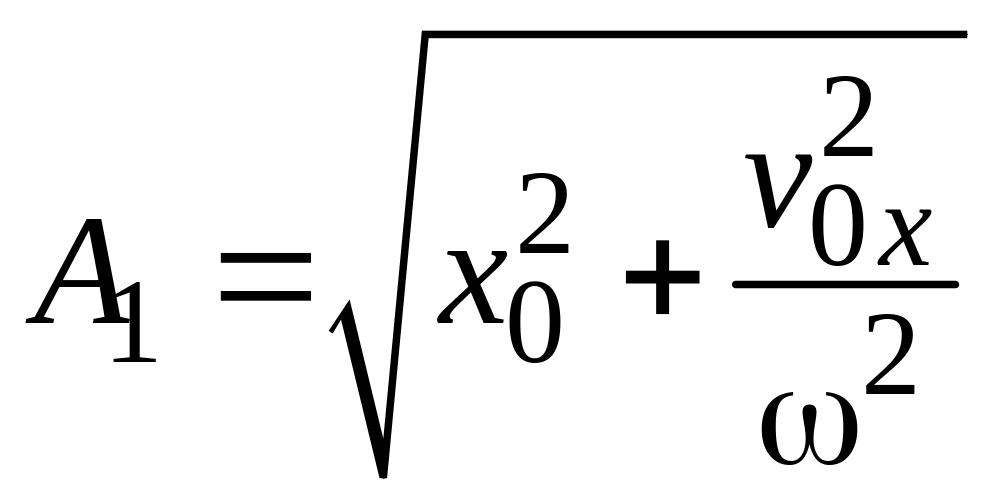 ,
,
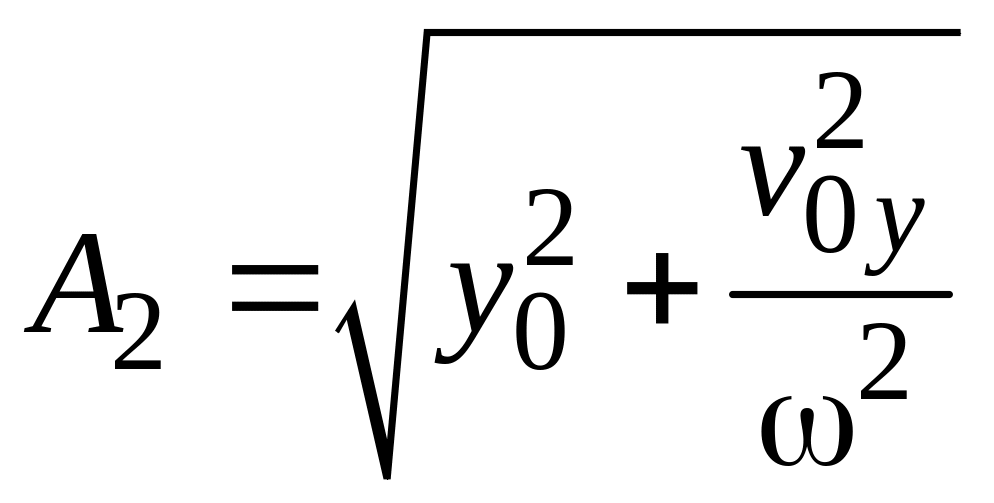 ,
,
![]() ,
,
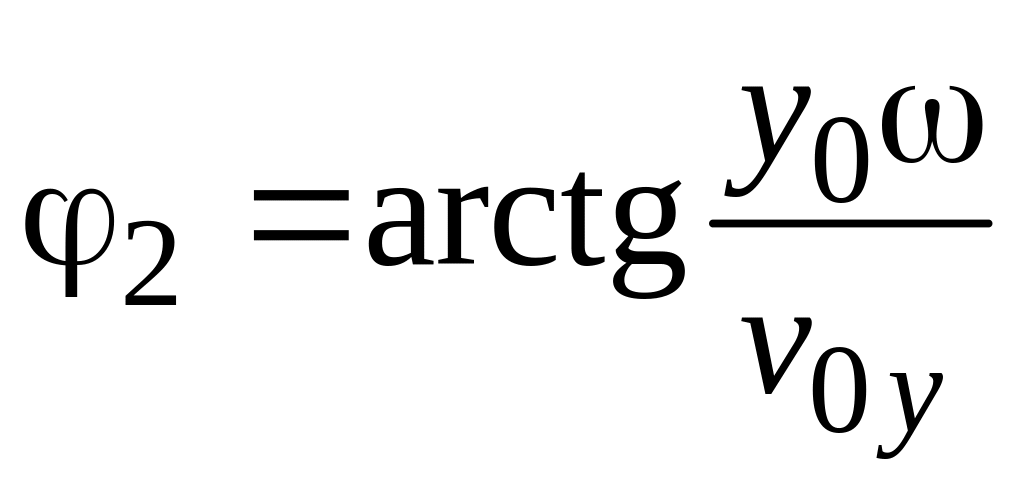 .
.
Из
найденных решений дифференциальных
уравнений движения следует, что в
направлении осей
![]() и
и
![]() точка совершает гармонические колебания
с частотой
и амплитудами
точка совершает гармонические колебания
с частотой
и амплитудами
![]() и
и
![]() .
Фазы колебаний
.
Фазы колебаний
![]() и
и
![]() .
Определим траекторию точки при наложении
взаимно перпендикулярных колебаний.
Для этого введем понятие разности фаз
.
Определим траекторию точки при наложении
взаимно перпендикулярных колебаний.
Для этого введем понятие разности фаз
![]() и уравнение движения по оси
запишем в виде
и уравнение движения по оси
запишем в виде
![]() .
.
Возведем в квадрат и сложим следующие уравнения:
![]() ,
,
![]()
В результате получим искомое уравнение траектории:
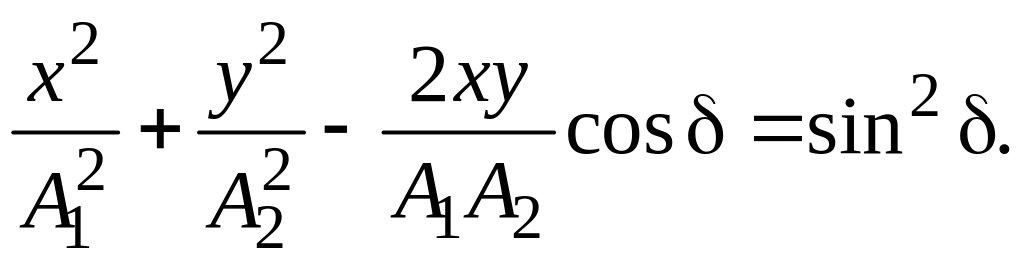
Это уравнение эллипса с центром в точке О. Плоскость эллипса и его размеры определяются начальными условиями, разность фаз определяет ориентацию эллипса в плоскости движения.
Ответ:
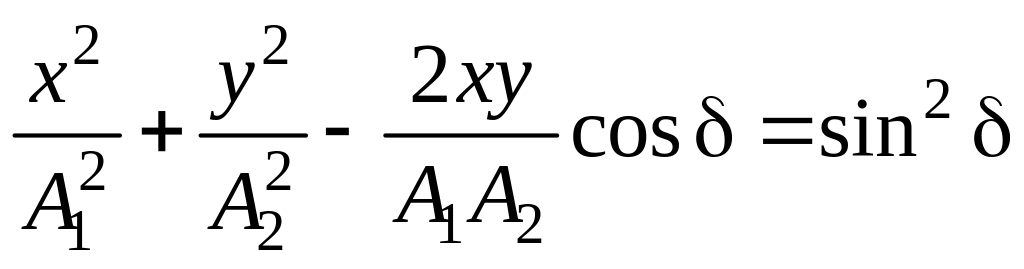 ,
где
,
где
![]() ,
,
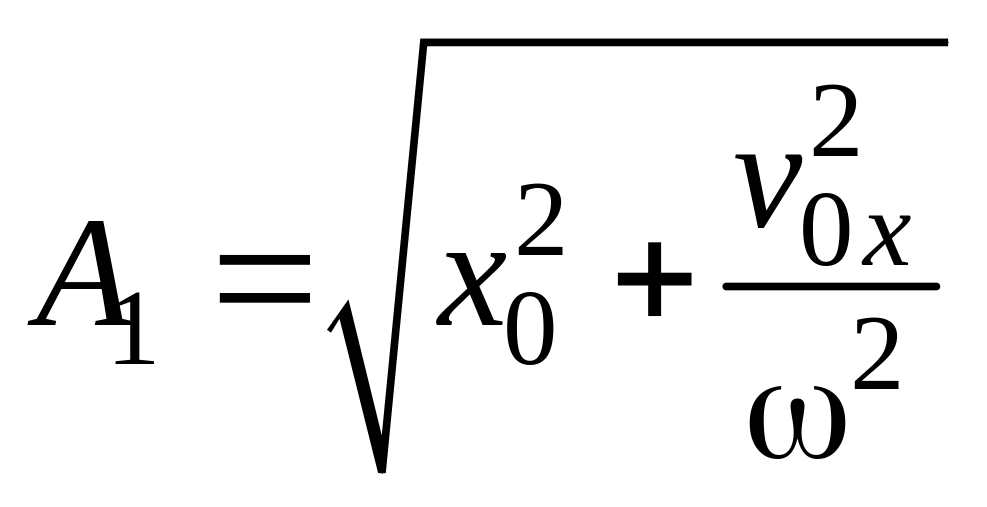 ,
,
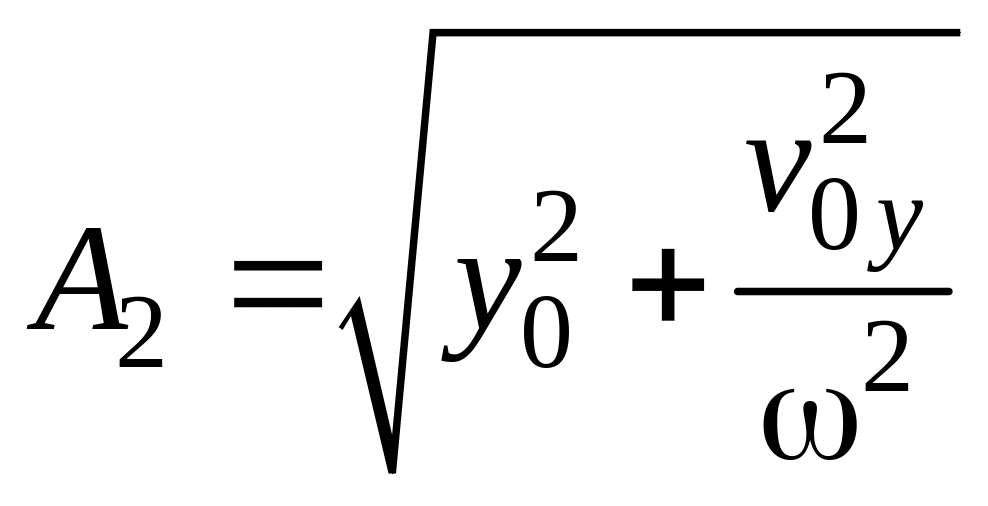 ,
,
![]() ,
,
![]() .
.
Задача 3
Однородный
стержень массой
и длины
совершает малые колебания в вертикальной
плоскости вокруг оси OZ, проходящей
через одну из его точек. К верхнему концу
стержня прикреплена пружинка жесткостью
![]() .
Найти расстояние между центром инерции
стержня и осью OZ, при котором частота
колебаний будет наибольшей. Трением
пренебречь.
.
Найти расстояние между центром инерции
стержня и осью OZ, при котором частота
колебаний будет наибольшей. Трением
пренебречь.
Решение.
Записываем уравнение вращательного движения стержня относительно оси OZ:
![]() (6.8)
(6.8)
где
![]() – момент
силы упругости;
– момент
силы упругости;
![]() – момент
силы тяжести (относительно точки О).
Момент инерции стержня относительно
оси OZ, согласно теореме Штейнера:
– момент
силы тяжести (относительно точки О).
Момент инерции стержня относительно
оси OZ, согласно теореме Штейнера:
![]()
где
![]() ;
– центр
инерции стержня (рис. 6.1)
;
– центр
инерции стержня (рис. 6.1)
Рис. 6.1 |
Спроектируем уравнение (5.8) на ось OZ, считая, что в рассматриваемый момент времени стержень движется от положения равновесия:
Предполагая колебания малыми, для силы упругости имеем
и уравнение (6.9) перепишется в виде |
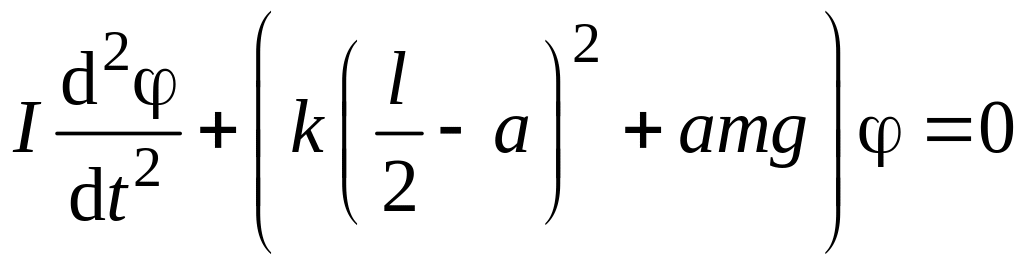 . (6.10)
. (6.10)
Уравнение (6.10) представляет собой дифференциальное уравнение гармонических колебаний с частотой
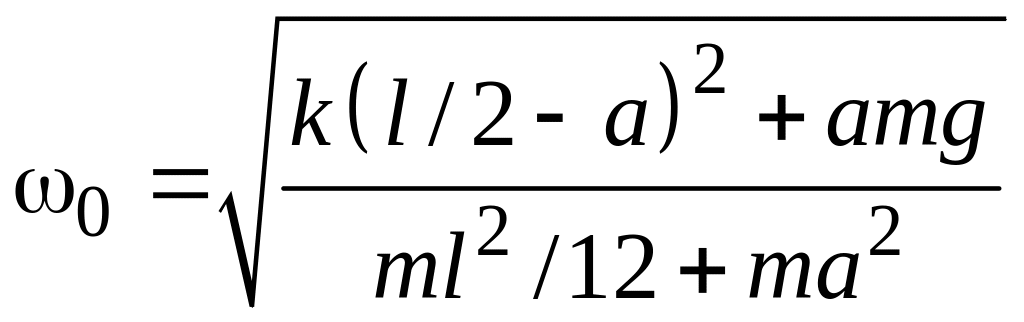 . (6.11)
. (6.11)
Чтобы
найти наибольшую частоту, продифференцируем
![]() по
по
![]()
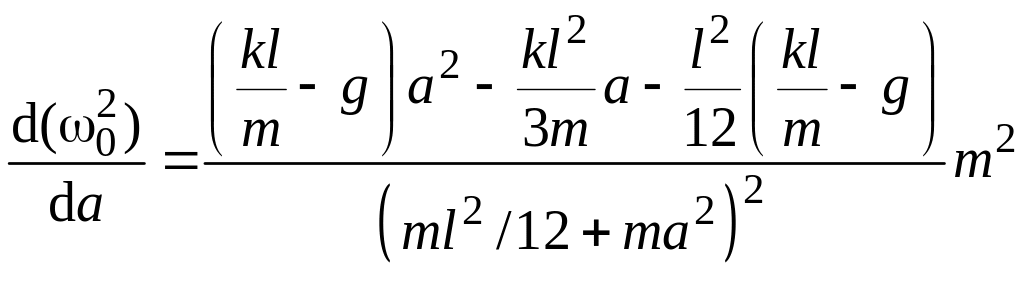 .
.
Приравнивая
производную нулю, находим требуемое
расстояние
![]()
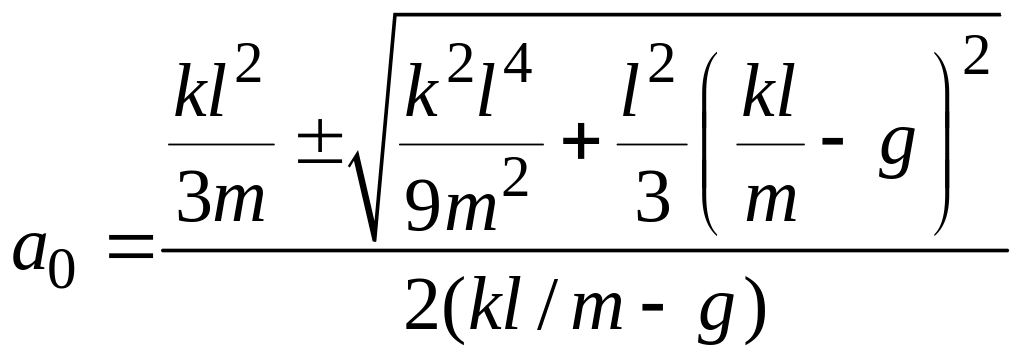 .
.
Учитывая, что по условию задачи , получаем
![]() .
.
Так
как
![]() ,
в числителе следует выбрать знак минус.
Тогда
,
в числителе следует выбрать знак минус.
Тогда
![]() .
Используя стандартные правила исследования
функции на экстремум, легко показать,
что найденное значение а0
соответствует максимуму функции
.
Используя стандартные правила исследования
функции на экстремум, легко показать,
что найденное значение а0
соответствует максимуму функции
![]() .
Подставляя
в выражение (6.11), окончательно получим
.
Подставляя
в выражение (6.11), окончательно получим
![]() .
.
Ответ:
![]() ,
,
![]() .
.
Задача 4
В
сплошном однородном цилиндре радиусом
|
Рис. 6.2 |
Решение.
Задача сводится к нахождению дифференциального уравнения колебаний цилиндра. С этой целью мысленно заполним полость тем же веществом, из которого сделан цилиндр. Образовавшийся таким образом сплошной однородный цилиндр назовем цилиндр 1, а цилиндр вдвое меньшего радиуса, заполняющего полость, – цилиндр 2. Массы цилиндров обозначим соответственно и . При повороте системы из положения равновесия на угол центр масс цилиндра 1 остается на прежней высоте, а колебания возникают за счет смещения центра масс цилиндра 2.
Запишем уравнение динамики вращательного движения для цилиндра относительно мгновенной оси, проходящей через точку О:
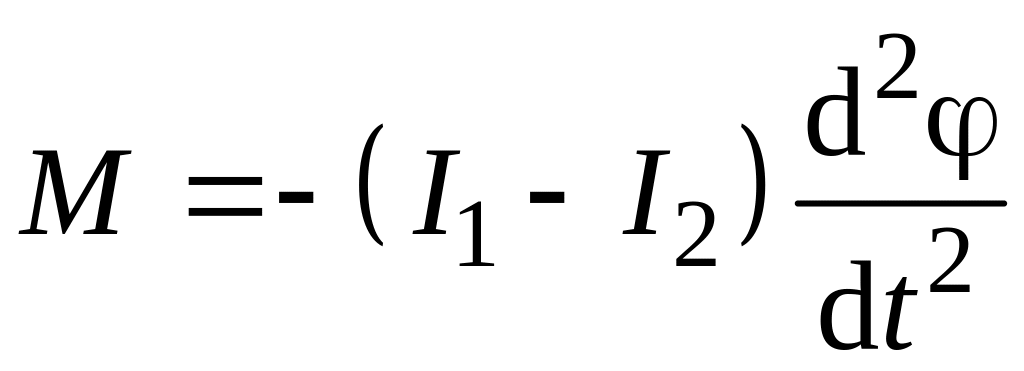 , (6.12)
, (6.12)
где
![]() – момент
силы тяжести цилиндра 2;
– момент
силы тяжести цилиндра 2;
![]() и
и
![]() – моменты
инерции цилиндров относительно мгновенной
оси.
– моменты
инерции цилиндров относительно мгновенной
оси.
При изменении угла величины и изменяются. Но для малых колебаний этими изменениями можно пренебречь и отнести и к тому моменту, когда система находится в положении равновесия. В этом положении с помощью теоремы Гюйгенса–Штейнера
![]() , (6.13)
, (6.13)
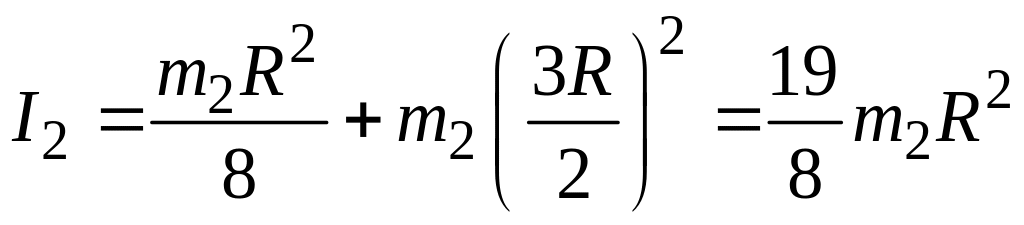 . (6.14)
. (6.14)
Момент силы тяжести цилиндра 2:
![]() .
(5.15)
.
(5.15)
Подставляя
(6.13)–(6.15) в (6.12) и учитывая, что
![]() ,
получаем дифференциальное уравнение
колебаний:
,
получаем дифференциальное уравнение
колебаний:
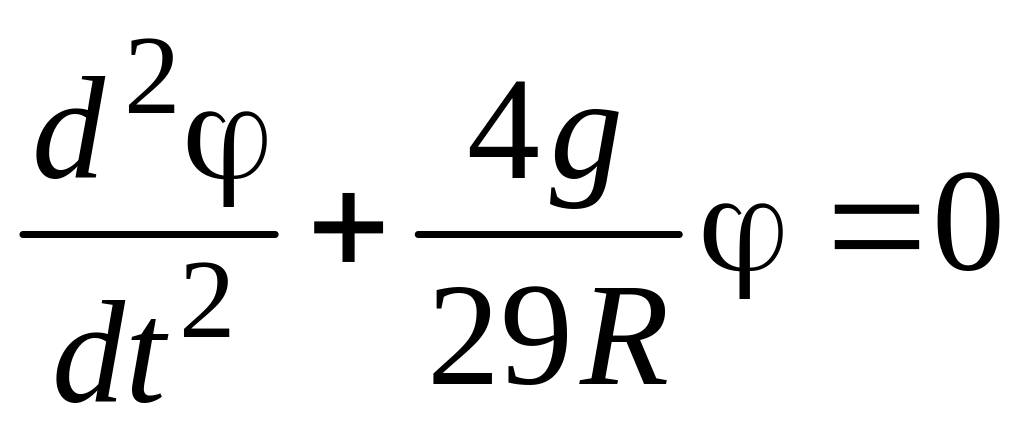 . (6.16)
. (6.16)
Из
теории собственных колебаний следует,
что квадрат собственной частоты колебаний
![]() .
Тогда период колебаний равен
.
Тогда период колебаний равен
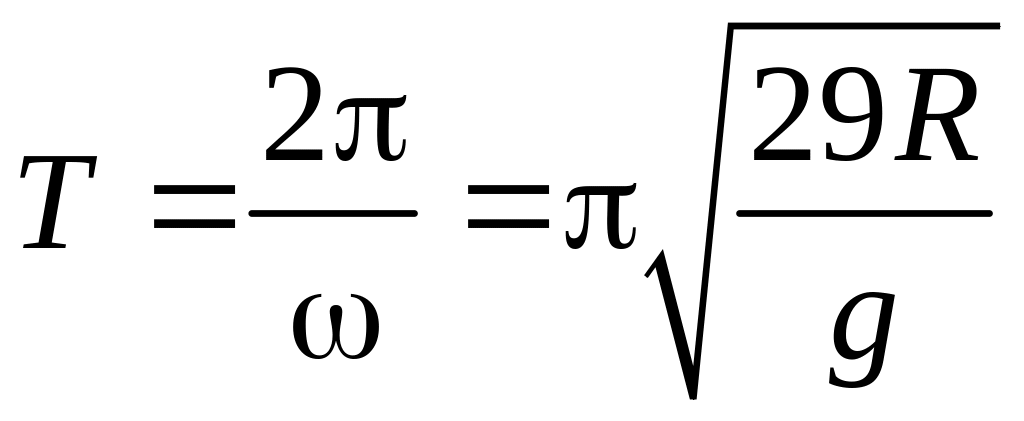 .
.
Ответ:
![]()
Задача 5
На
тележке укреплен горизонтальный
стержень, по которому может скользить
без трения муфта массой
![]() 1 кг.
К муфте прикреплены две
1 кг.
К муфте прикреплены две
пружины, общий коэффициент упругости которых = 1 Н/см. В состоянии равновесия центры масс муфты и тележки находились на одной вертикали. Какое возникает движение, если сместить муфту из положения равновесия на величину = 6 см и прикрепить нитью к тележке, а затем нить пережечь? Масса тележки без муфты |
Рис. 6.3 |
=5 кг, массой пружины пренебречь. Силу трения не учитывать.
Решение.
Если
отклонение муфты от общего центра масс
![]() ,
а отклонение тележки
,
а отклонение тележки
![]() ,
то
,
то
![]() (6.17)
(6.17)
Уравнение движения тележки
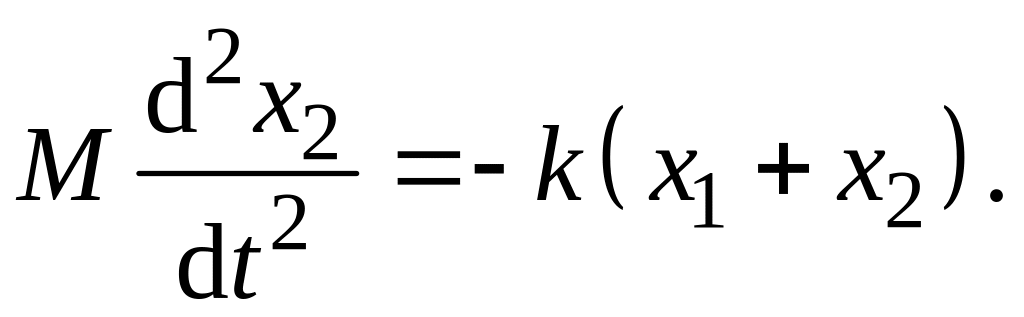 (6.18)
(6.18)
Заменяя из равенства (6.17), получаем дифференциальное уравнение колебаний:
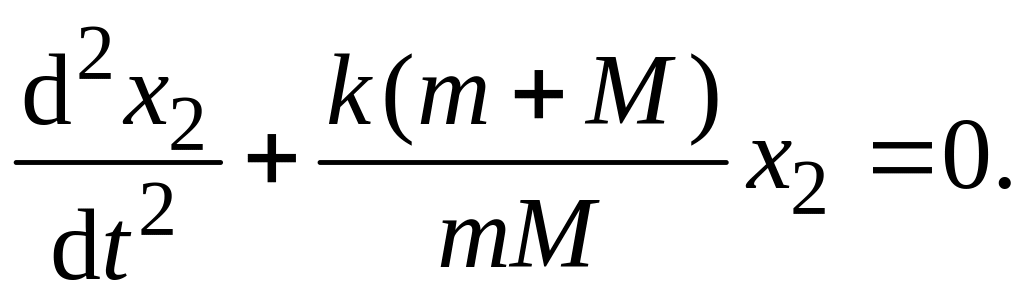 (6.19)
(6.19)
Аналогично для муфты
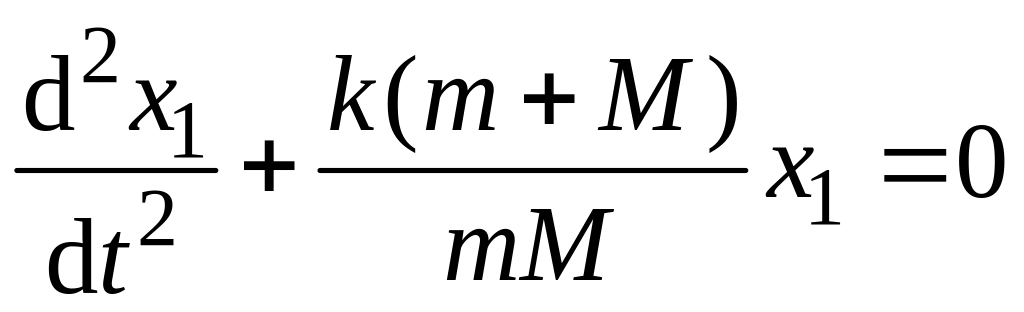 . (6.20)
. (6.20)
Следовательно,
будут происходить гармонические
колебания тележки и муфты с частотой
![]() с–1.
с–1.
Амплитуды
колебаний муфты
![]() = 5 см,
тележки
= 5 см,
тележки
![]() = 1 см.
= 1 см.
Ответ:
![]() =5 см,
=5 см,
![]() =1 см.
=1 см.
Задача 6
Затухающие колебания материальной точки массой происходят в плоскости XOY по закону
![]()
![]()
Найти:
а) путь, пройденный частицей до полной остановки;
б) логарифмический декремент затухания, при котором этот путь
минимален.
Решение.
Прежде всего найдем величину скорости частицы как функцию времени:
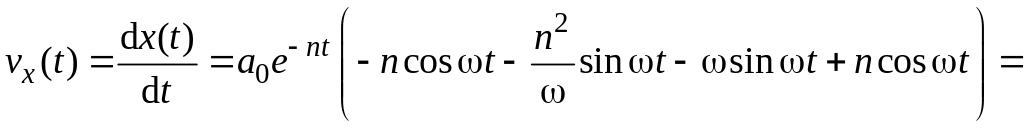
![]()
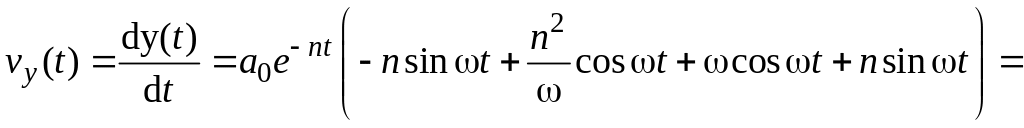
![]()
Следовательно, величина скорости
![]() .
.
Путь,
пройденный материальной точкой к моменту
времени
![]()
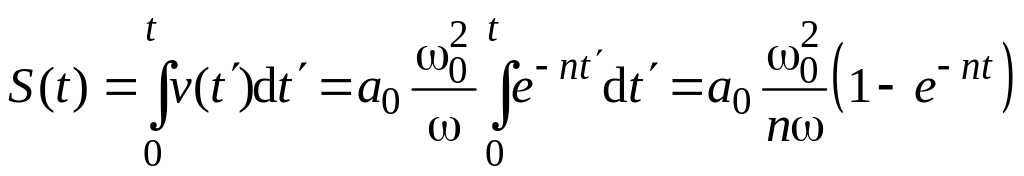 .
.
Путь, пройденный частицей до полной остановки:
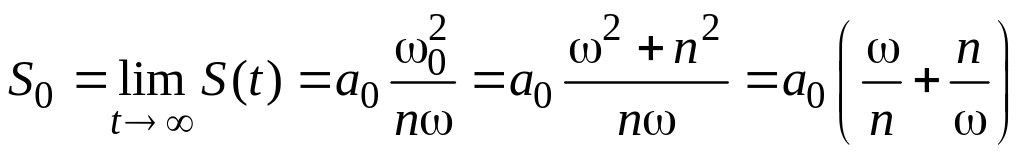 . (6.21)
. (6.21)
Из
выражения (6.21) следует, что путь
![]() минимален, когда
минимален, когда
![]() Учитывая, что логарифмический декремент
затухания
получаем
Учитывая, что логарифмический декремент
затухания
получаем
![]()
Ответ:
а)
![]() б)
б)
![]()
Задача 7
Груз
массой
подвешен на пружине жесткости
![]() .
На него действует возмущающая вертикальная
сила
.
На него действует возмущающая вертикальная
сила
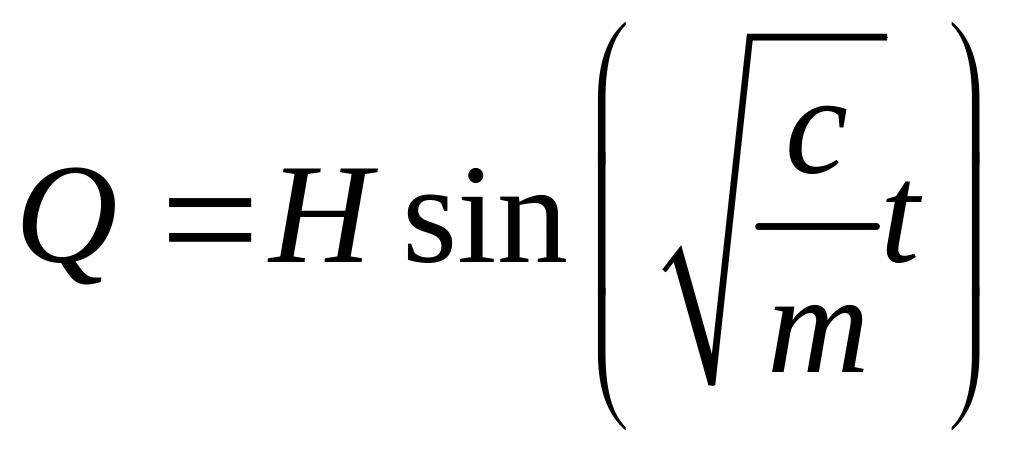 и сила сопротивления
и сила сопротивления
![]() Определить амплитуду вынужденных
колебаний груза.
Определить амплитуду вынужденных
колебаний груза.
Решение.
Запишем дифференциальное уравнение вертикальных колебаний груза, считая ось направленной вертикально вверх:
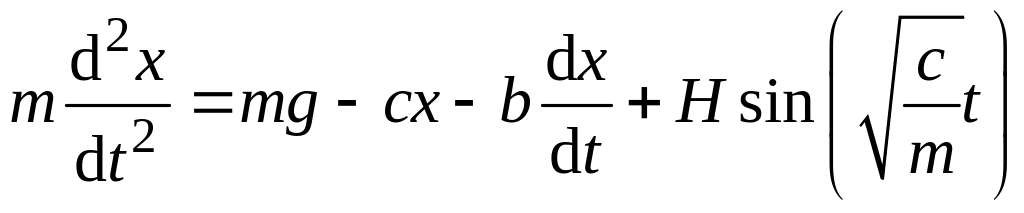 ,
,
или
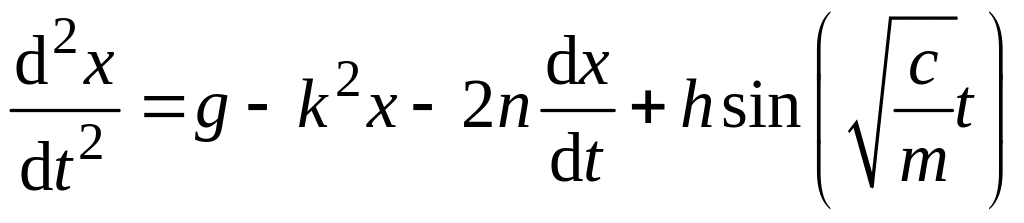 ,
,
где
![]()
![]()
![]() .
.
Решение
дифференциального уравнения вкладывается
из общего решения
соответствующего однородного уравнения
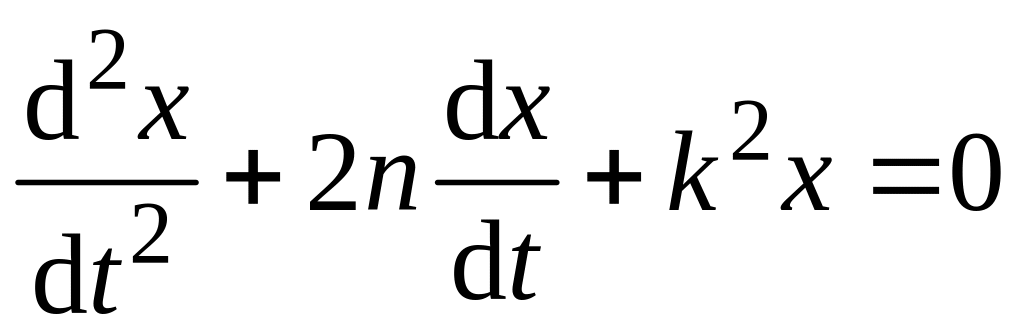 и частного решения
неоднородного уравнения
и частного решения
неоднородного уравнения
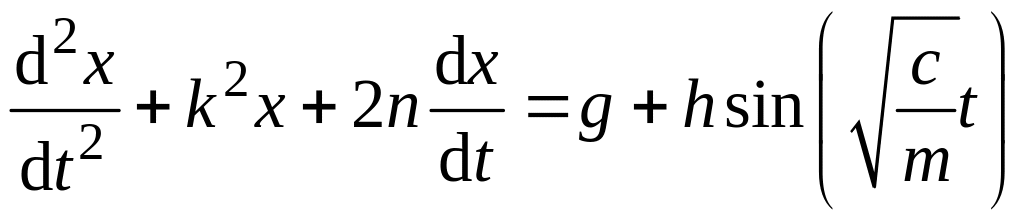 ;
– вынужденные
колебания. Будем искать
в виде
;
– вынужденные
колебания. Будем искать
в виде
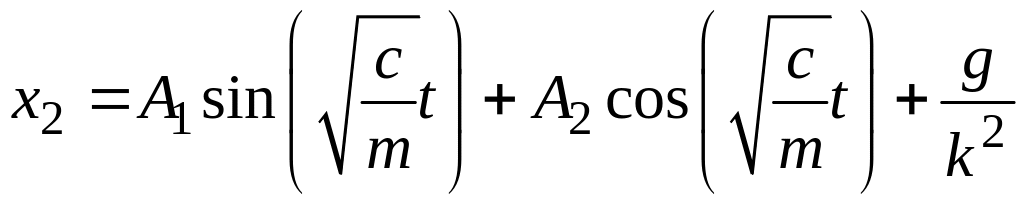 .
.
Для определения и найдем:
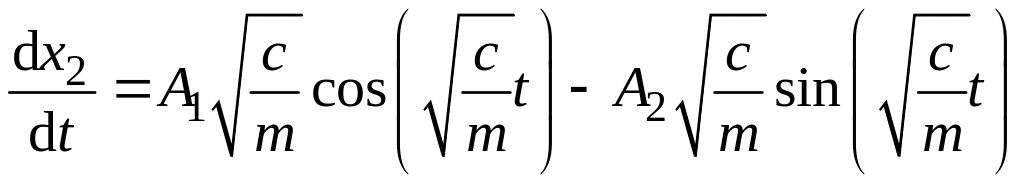 ,
,
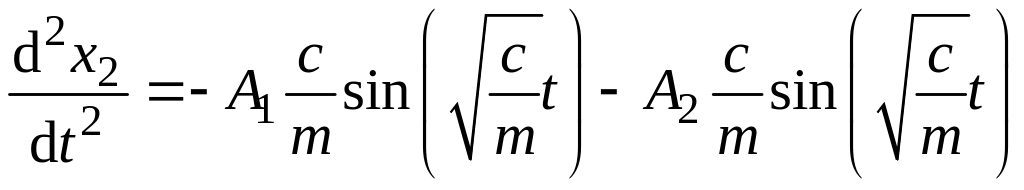
и подставим в неоднородное
дифференциальное уравнение. Приравнивая
в полученном выражении коэффициенты
при
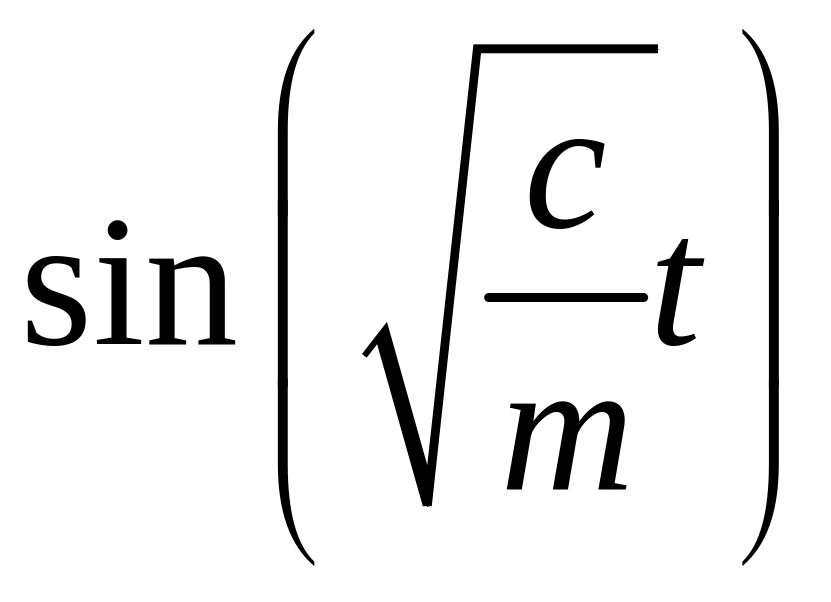 и
и
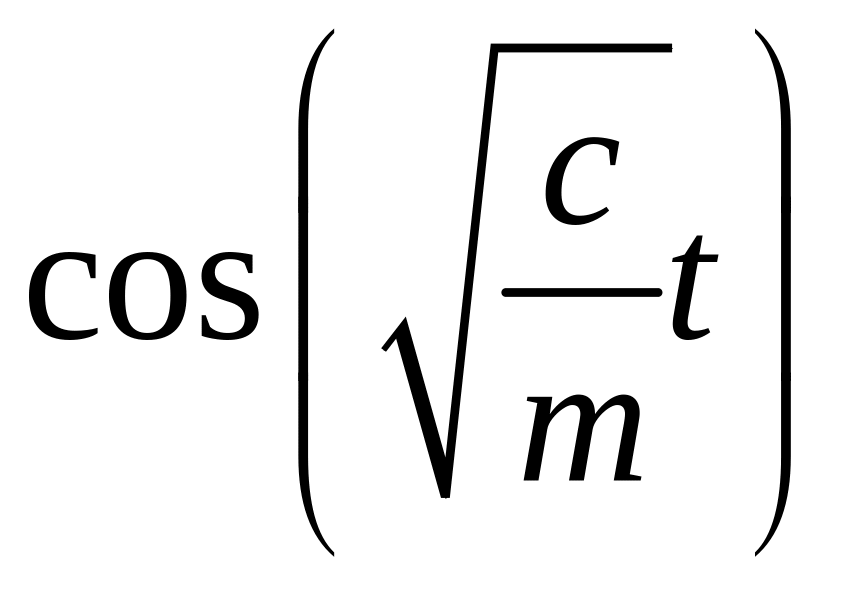 ,
получаем:
,
получаем:
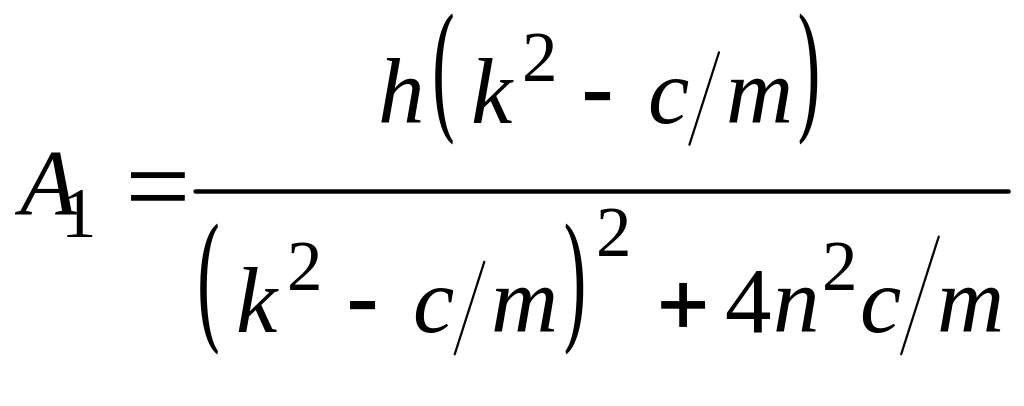 ,
,
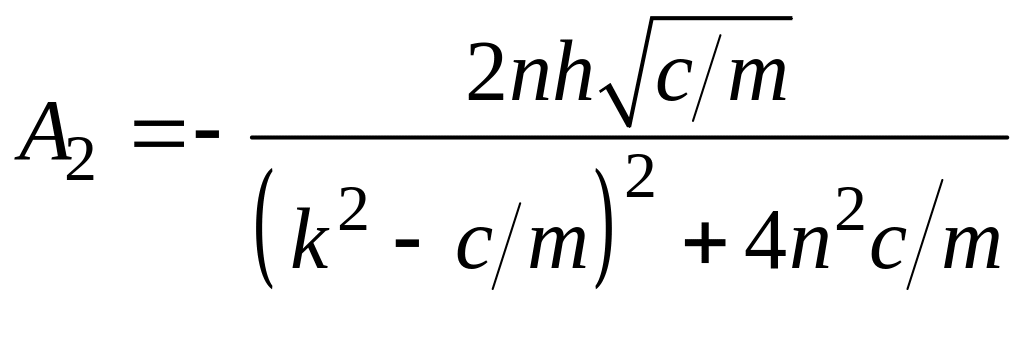 .
.
Введем обозначения:
 ,
,
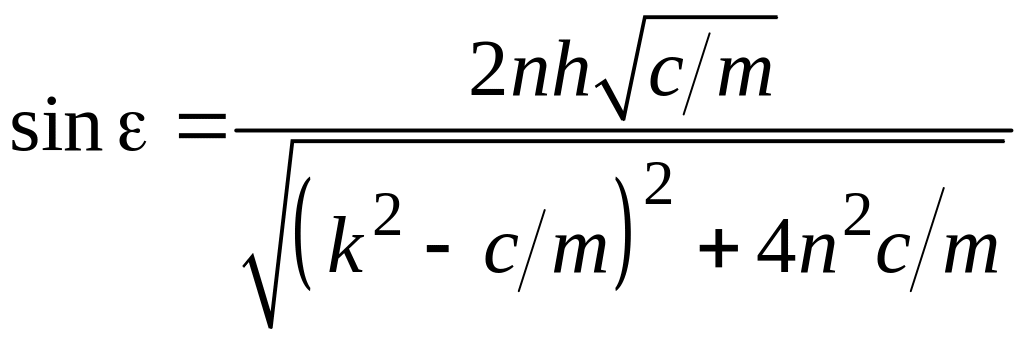 ,
,
тогда
![]() ,
,
где
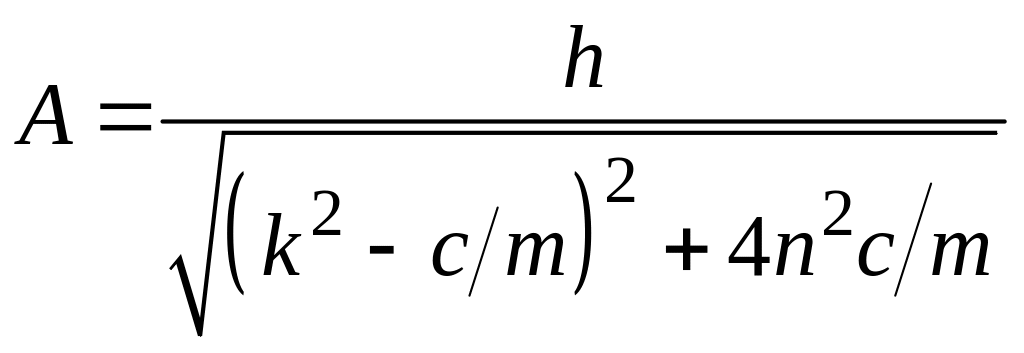 – амплитуда колебаний.
– амплитуда колебаний.
Учитывая значения
![]() ,
,
![]() ,
находим
,
находим
![]() .
.
Ответ:
![]()
![]()
Задача 8
Материальная
точка массой
![]() кг
движется по горизонтальной прямой под
действием силы
кг
движется по горизонтальной прямой под
действием силы
![]() Н. Кроме того, на точку действует
возмущающая сила
Н. Кроме того, на точку действует
возмущающая сила
![]() Н. По какому закону движется точка, если
в начальный момент времени
Н. По какому закону движется точка, если
в начальный момент времени
![]() ;
;
![]() м/с
и возмущающая сила в начале движения
совпадает по направлению со скоростью
м/с
и возмущающая сила в начале движения
совпадает по направлению со скоростью
![]() ?
?
Решение.
Составим дифференциальное уравнение движения точки, направив ось по ее траектории точки:
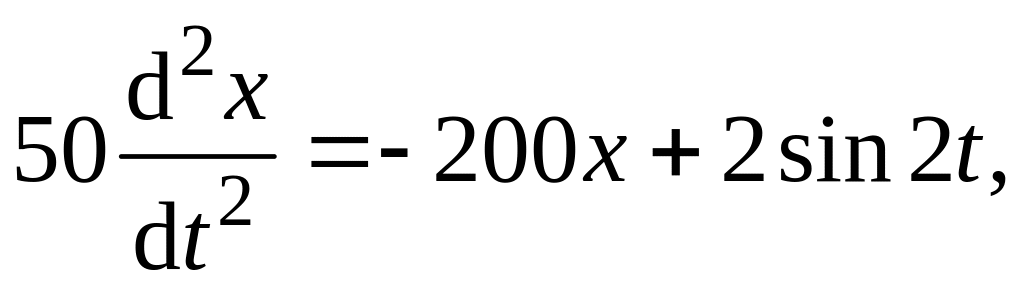 или
или
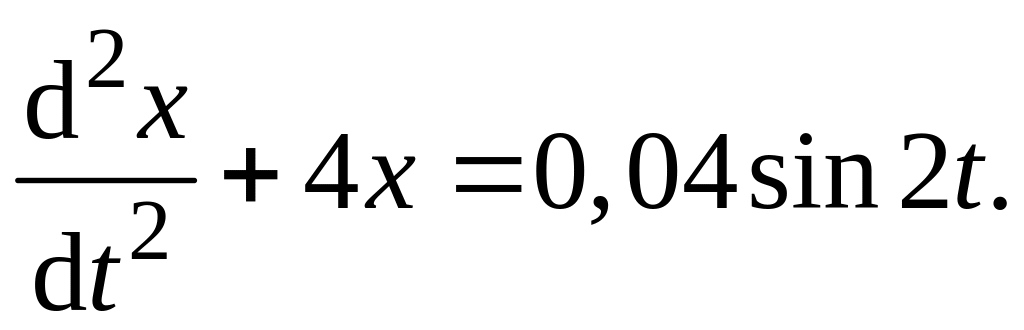
Частота
собственных колебаний (![]() )
и частота вынуждающей силы (
)
и частота вынуждающей силы (![]() )
совпадают, следовательно, имеет место
явление резонанса. Общее решение
неоднородного уравнения найдем как
сумму
решения соответствующего однородного
уравнения
)
совпадают, следовательно, имеет место
явление резонанса. Общее решение
неоднородного уравнения найдем как
сумму
решения соответствующего однородного
уравнения
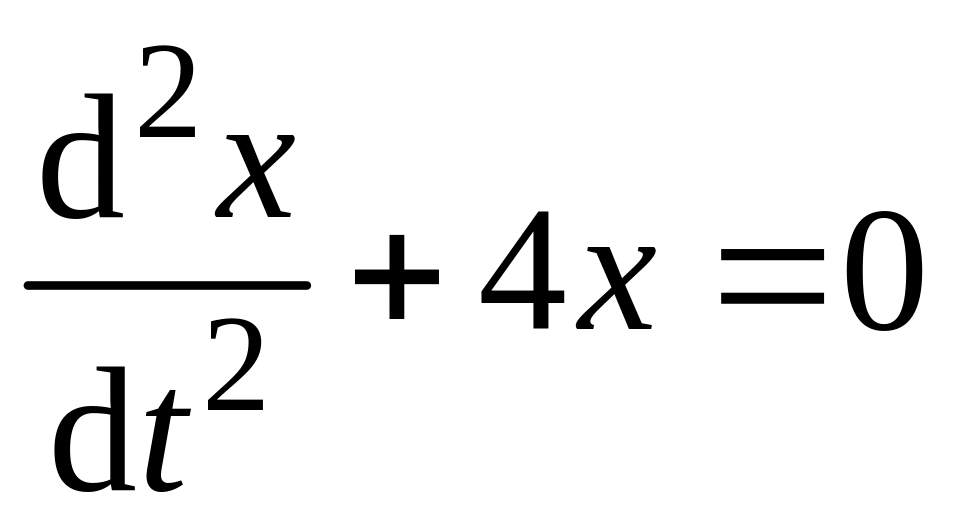 и честного решения
неоднородного уравнения. Будем считать
и честного решения
неоднородного уравнения. Будем считать
![]() ;
;
![]() Для определения
Для определения
![]() найдем
найдем
![]()
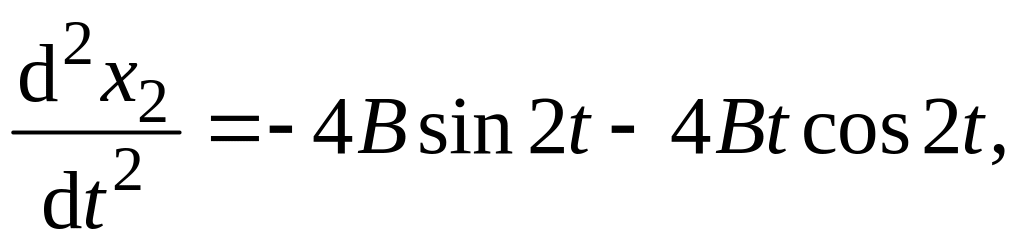
и подставим в неоднородное
уравнение. Получаем
![]() ;
тогда
;
тогда
![]() Используя начальные условия
Используя начальные условия
![]()
![]() .
Имеем:
.
Имеем:
![]() ,
,
![]()
Ответ:
![]()
Задача 9
Найти
уравнение стоячей волны в однородном
тонком стержне длиной
![]() один из торцов которого закреплен, а
также спектр его собственных частот.
Плотность вещества стержня
,
модуль Юнга
один из торцов которого закреплен, а
также спектр его собственных частот.
Плотность вещества стержня
,
модуль Юнга
![]()
Решение.
Пусть
на свободном торце стержня, находящемся
в начале координат, созданы гармонические
колебания
![]() Тогда при условии пренебрежения
затуханием вдоль стержня, лежащего на
оси OX, распространяется упругая
волна
Тогда при условии пренебрежения
затуханием вдоль стержня, лежащего на
оси OX, распространяется упругая
волна
![]() ,
,
![]() (6.22)
(6.22)
которая затем отражается
от закрепленного торца
![]() .
В каждой точке волнового поля между
торцами будут складываться колебания
от падающей и отраженной волны. Уравнение
отраженной волны имеет вид
.
В каждой точке волнового поля между
торцами будут складываться колебания
от падающей и отраженной волны. Уравнение
отраженной волны имеет вид
![]() ,
,
где
![]() – сдвиг
колебаний по фазе в отраженной волне в
точке
по сравнению с колебаниями в точке O:
– сдвиг
колебаний по фазе в отраженной волне в
точке
по сравнению с колебаниями в точке O:
![]() (6.23)
(6.23)
Второе слагаемое в формуле (6.23) обусловлено неподвижностью точек закрепленного в точке торца, которая будет обеспечена, если колебания в точке в падающей и отраженной волнах будут в противофазе. Таким образом,
![]() (6.24)
(6.24)
Складывая уравнения (6.22) и (6.24), получаем уравнение стоячей волны
![]()
![]() . (6.25)
. (6.25)
Спектр
собственных частот стержня
![]() найдем из условия синфазности колебаний
в отраженной волне в точке O
с колебаниями источника, т. е.
найдем из условия синфазности колебаний
в отраженной волне в точке O
с колебаниями источника, т. е.
![]()
![]() .
.
или
![]()
Отсюда
![]() ,
,
![]() . (6.26)
. (6.26)
В
продольной упругой волне
![]() .
Поэтому
.
Поэтому
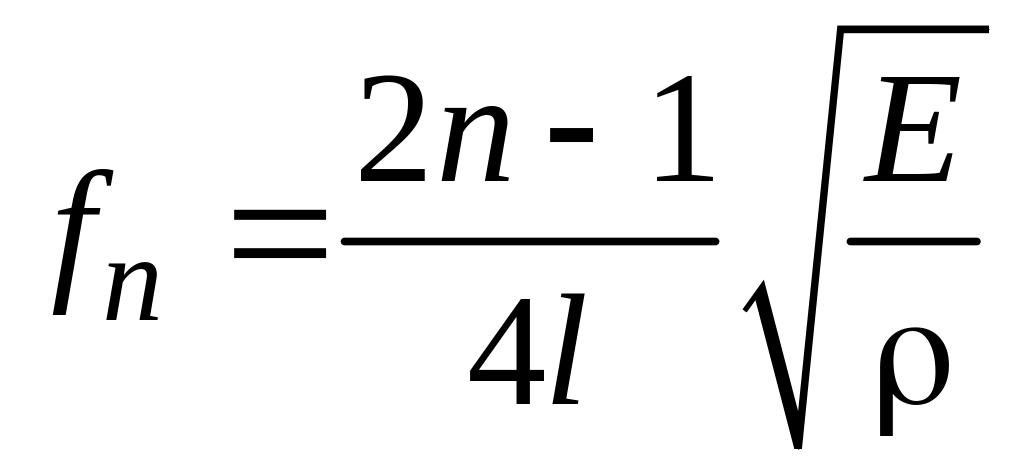 ,
.
,
.
Если
частота колебаний равна
,
то, согласно (6.26),
![]() ,
и уравнение стоячей волны (6.25) примет
вид
,
и уравнение стоячей волны (6.25) примет
вид
![]()
Ответ:
![]()
Задача 10
Найти
энергию упругой стоячей волны в однородном
тонком стержне массой
![]() один конец которого закреплен, если на
свободном конце созданы колебания с
собственной частотой
и амплитудой
один конец которого закреплен, если на
свободном конце созданы колебания с
собственной частотой
и амплитудой
![]()
Решение.
Энергия упругой волны определяется формулой
![]()
где
![]() – плотность
энергии;
– плотность
энергии;
![]() – область
волнового поля.
– область
волнового поля.
В нашем случае
;
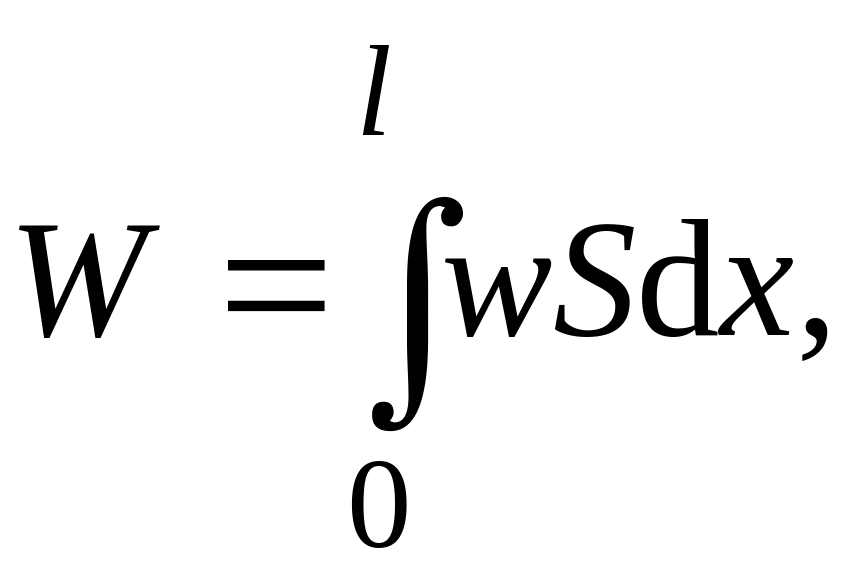 (6.27)
(6.27)
где
– плотность
вещества стержня;
![]() – площадь
его поперечного сечения.
– площадь
его поперечного сечения.
Из решения предыдущей задачи следует
![]()
где
![]() ;
;
![]() .
Поэтому с учетом того, что
.
Поэтому с учетом того, что
![]() плотность энергии волны
плотность энергии волны
![]()
![]() .
.
Подставляя выражение для в формулу (6.27), находим
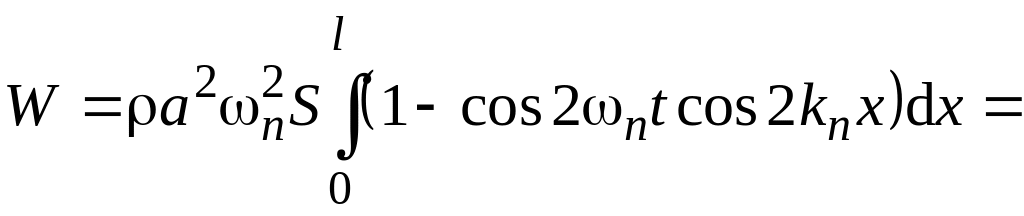
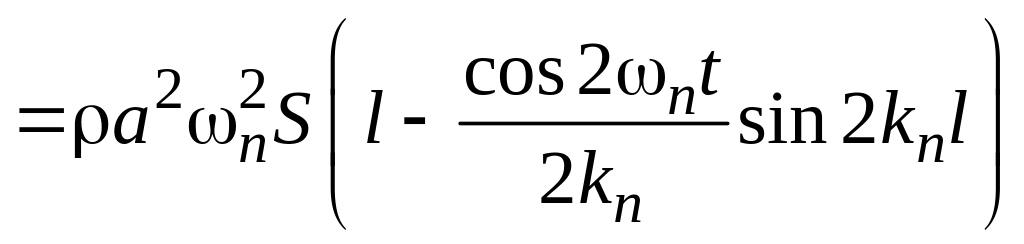 .
.
Но поскольку для
собственной частоты
![]() то
то
![]() и
и
![]() .
.
Ответ:
![]()
Задача 11
Плоская
волна
![]() распространяется в упругой среде
плотностью
.
Найти средний за период колебаний поток
энергии плоской волны через поверхность
полусферы, задаваемой уравнением
распространяется в упругой среде
плотностью
.
Найти средний за период колебаний поток
энергии плоской волны через поверхность
полусферы, задаваемой уравнением
![]() .
.
Решение.
Вектор
плотности потока энергии
![]() выражается через плотность энергии
и скорость распространения волны
выражается через плотность энергии
и скорость распространения волны
![]() следующим образом:
следующим образом:
![]() ,
,
где
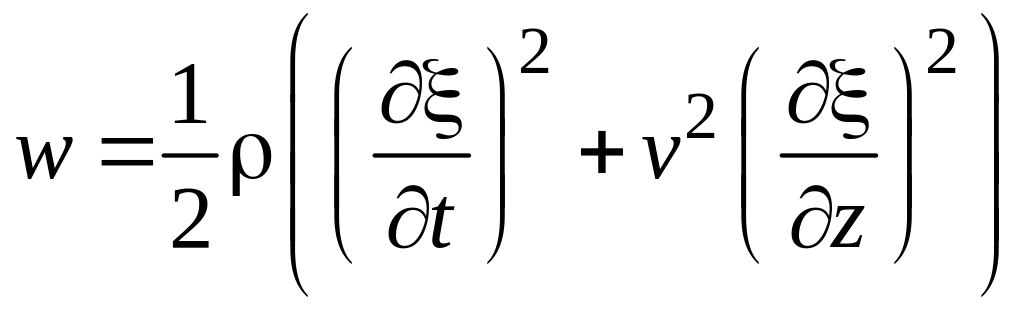 ; (6.28)
; (6.28)
![]() .
.
Дифференцируя
уравнение плоской волны по
и
![]() получаем:
получаем:
![]() ; (6.29)
; (6.29)
![]() . (6.30)
. (6.30)
Подставляя выражения (6.29) и (6.30) в (6.28), находим
![]()
Следовательно,
![]() .
.
Поток энергии через полусферу (см. рис. 6.4)
Рис. 6.4 |
Элемент площади поверхности сферы |
радиусом
в сферических координатах имеет вид
![]() .
Поэтому, учитывая, что
.
Поэтому, учитывая, что
![]() ,
получаем
,
получаем
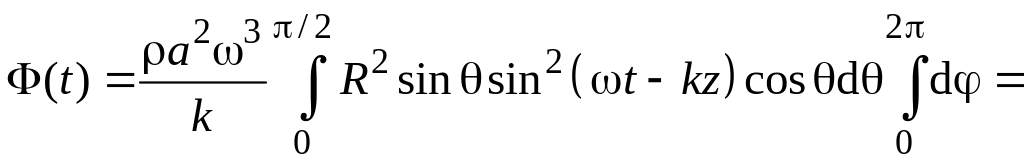
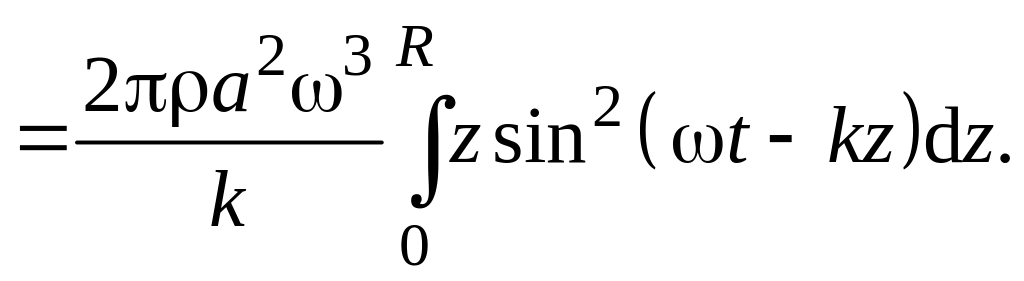 (6.31)
(6.31)
По определению средний за период колебаний поток энергии
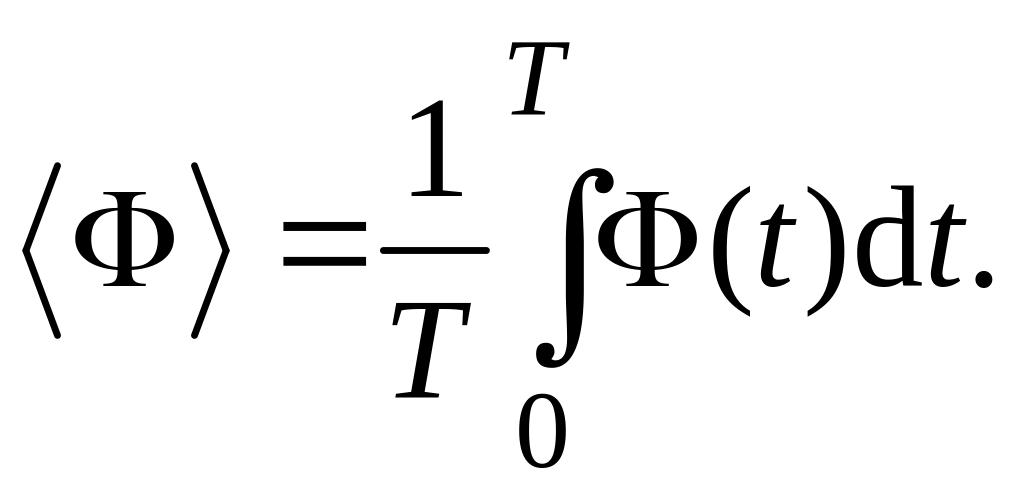 (6.32)
(6.32)
Подставляя выражение (6.31) в (6.32), находим
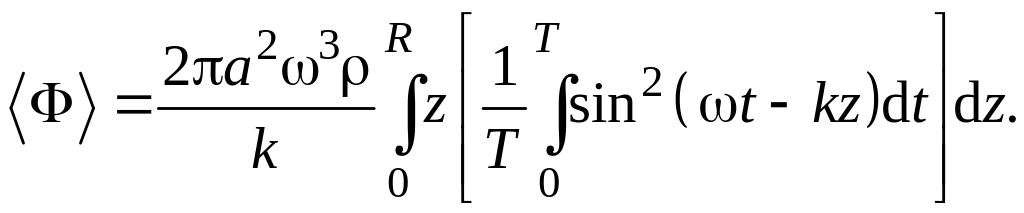
Так как
![]()
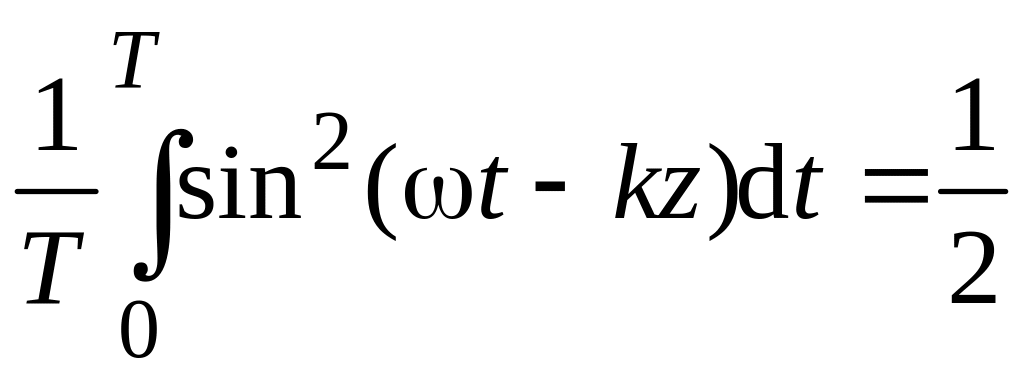 .
.
Следовательно,
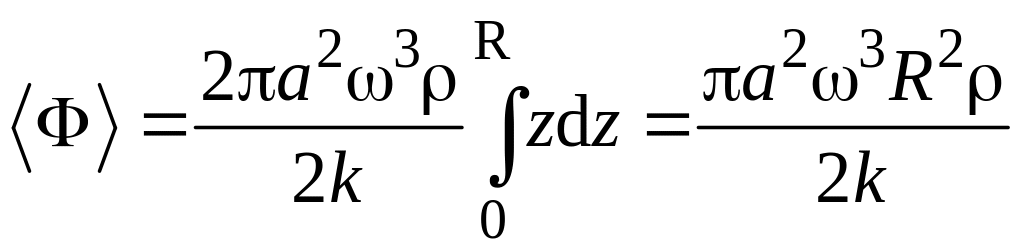 .
.
Ответ:
![]()





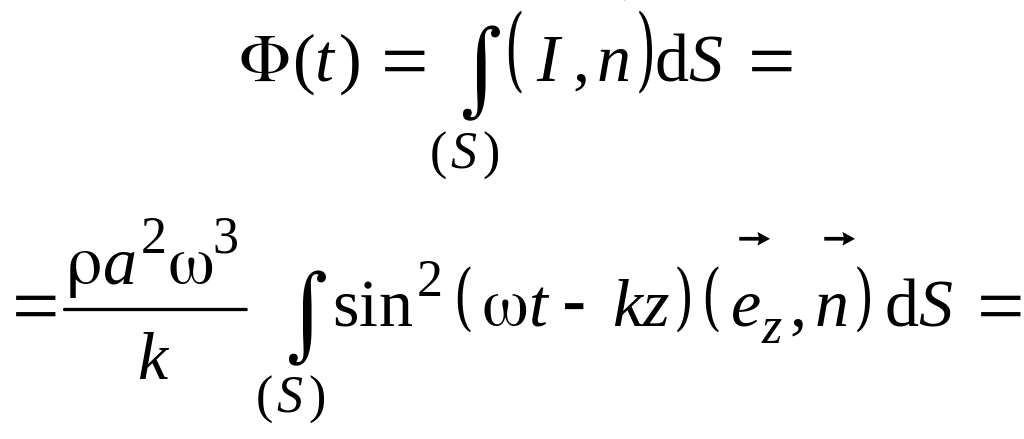
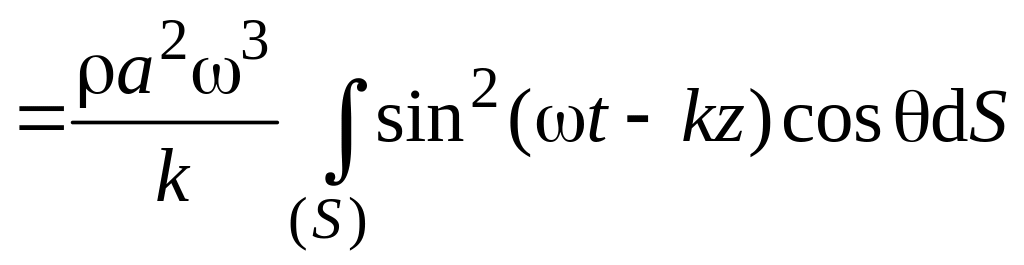 .
.