6. Колебания и волны

____________________________________________________________________________________________________________________________________________________________________________________________________________________________

Краткая теория и методические указания

Важными характеристиками колебательного движения являются их форма, периодичность и т. д. Эти характеристики, независимо от природы колебаний, присущи как колебаниям механическим, так и электрическим, тепловым. Что же касается причин, вызывающих и обусловливающих колебания, то они определяются природой колебательной системы. Далее будем рассматривать механические колебательные системы, например, колебания системы при выводе ее из положения равновесия при наличии внутренних упругих взаимодействий, а затем предоставленной самой себе, которые называются свободными. Характер свободных колебаний зависит от того, насколько большим будет сопротивление движению. Если таковым можно пренебречь, то колебания можно считать чисто гармоническими, с неизменной амплитудой, а при наличии трения амплитуда колебаний будет с течением времени уменьшаться по определенному закону, и колебания нельзя представить только гармонической функцией. В первом случае колебания обычно называют собственными, во втором – затухающими.

Тело (материальная точка) массой двигается по прямой так, что положение ее описывается координатой На точку действует упругая сила где  – положительная постоянная. В точке сила При уходе точки вправо ( ) сила , т. е. действует в направлении точки равновесия О. При уходе тела влево ( ) сила положительна, т. е. снова действует в направлении точки О. Таким образом, всякий раз сила стремится вернуть тело в точку О, которая называется положением равновесия. Примером может служить тело на конце горизонтально расположенной пружины.

Уравнение движения тела, движущегося под действием силы имеет следующий вид: 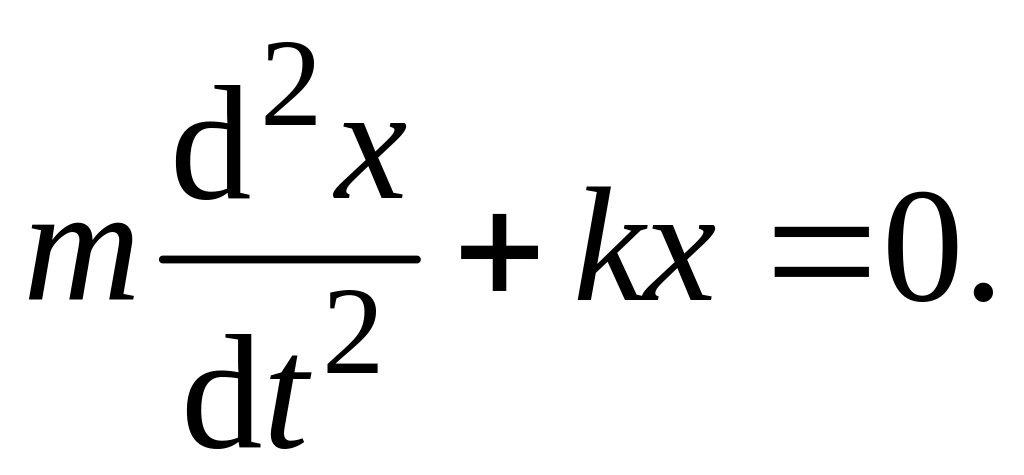Это дифференциальное уравнение второго порядка для отыскания зависимости . Обычно его записывают в ви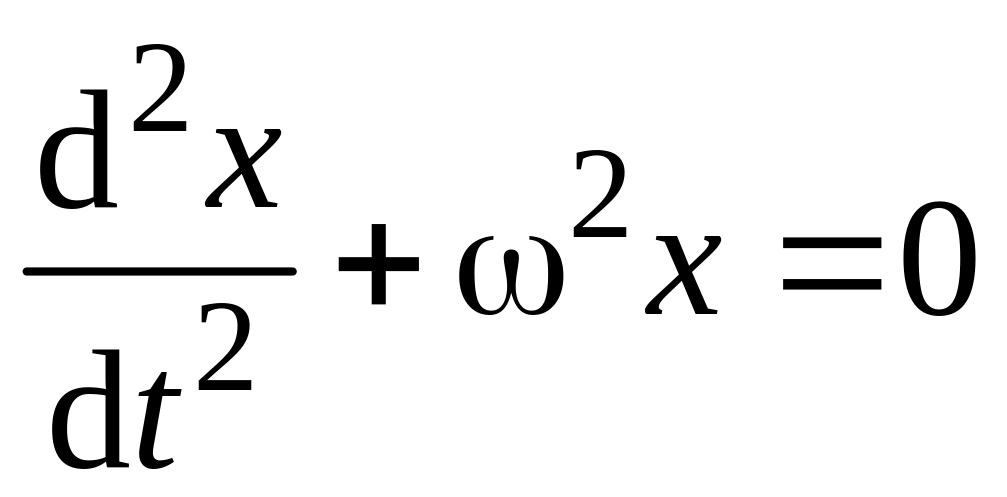де , где  – заданная константа.

Решением этого уравнения является выражение

(6.1)

Здесь  – амплитуда колебания,  – его фаза, где  – частота,  – начальная фаза (при ). Так как есть периодическая функция времени формула (6.1) описывает периодически меняющуюся координату, и движение точки является периодическим –колебательным. Колебания, совершающиеся по закону косинуса (или синуса), т. е. когда закон движения имеет вид (6.1), называются гармоническими.

Характеристика зависит от свойств точки (массы) и действующей силы (коэффициента упругости), и зависят от начальных условий. Поскольку изменяется от –1 до +1, значение определяется как координата при фазе …; т. е. как максимальное отклонение от положения равновесия 0.

Косинус есть периодическая функция своего аргумента  =  , где  – целое число. Поэтому если вместо взять момент времени , такой, что аргумент косинуса отличается от аргумента на величину то т. е. есть период функции . Из условия следует, что или  – период колебаний. На равне с циклической частотой часто используют линейную частоту . Из определения следует, что период колебаний зависит только от частоты (свойств колебательной системы) и не зависит от амплитуды.

Имея дело с законом движения колеблющейся точки, например, в виде (6.1), нужно помнить, что значение при этом откладывают не от произвольно выбранного начала координат, как это было в других задачах, а обязательно от точки равновесия. Нетрудно доказать, что если при горизонтально расположенной пружине положение равновесия, от которой велся отсчет координат, находился в точке О, то при вертикально подвешенной пружине положение равновесия определяется из условия Таким образом, положение равновесия теперь находится в точке , отстоящей от точки О на расстоянии

Не всегда колебания происходят под действием упругих сил. Примером может служить плоский математический маятник, движение которого происходит под действием силы тяжести и реакции связи. Координата от угла отклонения от положения равновесия зависит гармонически, а от времени – негармонически. В самом деле, для того чтобы была представлена в виде необходимо, чтобы угол был пропорционален (линейно зависел от времени), иначе говоря, В действительности этого нет: положение равновесия тело проходит быстро, вблизи наибольшего отклонения движется медленно, останавливается и возвращается (здесь изменяет знак).

Таким образом, колебания маятника в общем случае не являются гармоническими, однако если угол мал, то оказывается, что закон движения маятника приблизительно описывается гармонической функцией времени. При малом угле результирующая сила направленная по касательной к траектории (окружности), приблизительно совпадает со своей проекцией на ось : . Поскольку при малом значении ( , ), то где знак минус указывает на то, что сила направлена в сторону, противоположную увеличению значения Положение маятника однозначно определяется координатой , причем , и при малых значениях . Для определения координаты запишем уравнени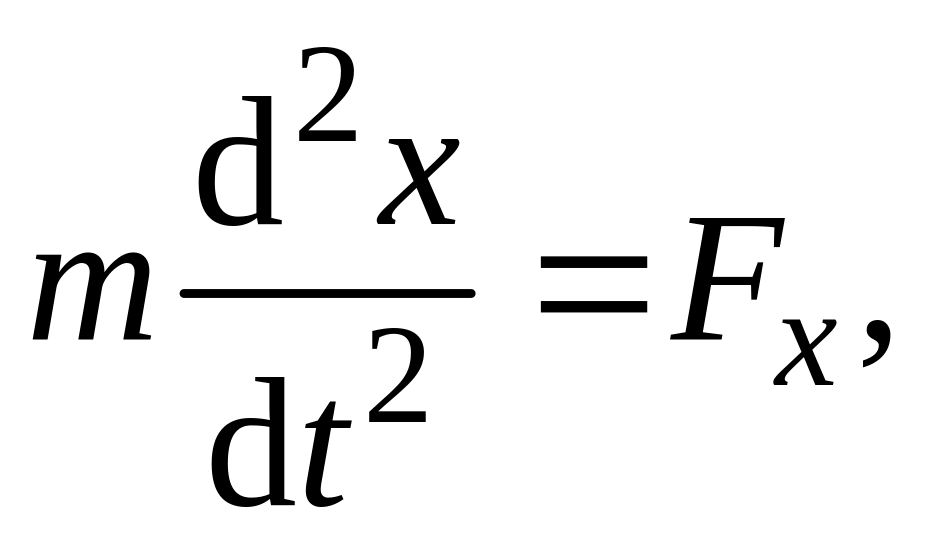е т. е. 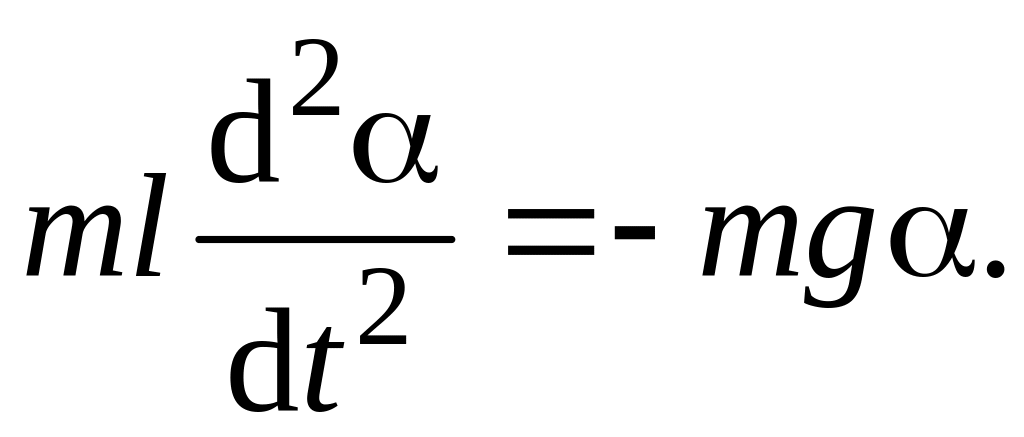Уравнение 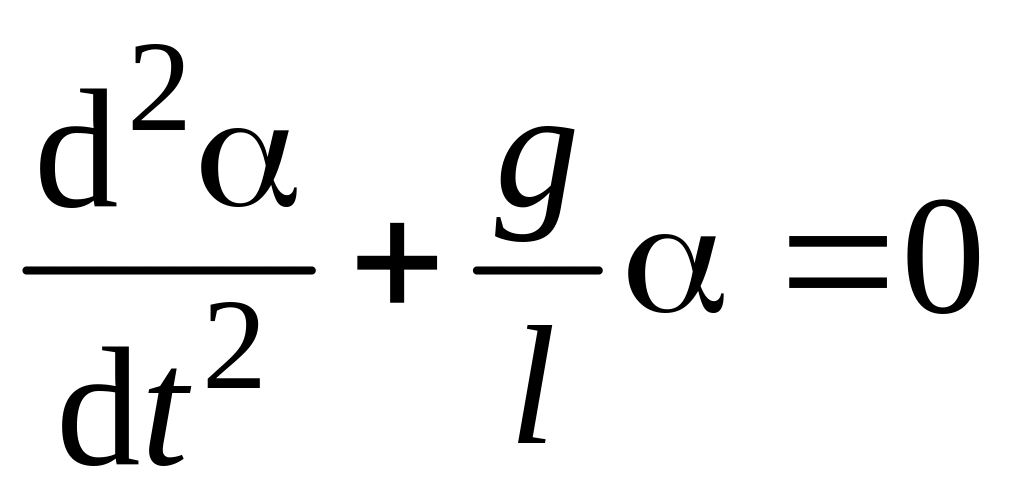является уравнением движения для гармонических колебаний математического маятника, частота которого Следовательно, решением данного уравнения является , где амплитуда и начальная фаза определяются из начальных условий. Приблизительно . Период колебаний ,

В задачах о математическом маятнике необходимо учитывать, что если маятник находится в неинерциальной системе отсчета, т. е. в системе отсчета, которая движется относительно инерциальной системы с некоторым ускорением то период его колебаний где  – ускорение свободного падения в неинерциальной системе отсчета. Это ускорение можно найти из векторного уравнения , где  – ускорение свободного падения в инерциальной системе отсчета.

Выясним теперь характер колебаний рассмотренной системы при наличии трения. При этом будем полагать, что силы трения пропорциональны скорости тела и противоположно ей направлены. Такими силами, например, являются силы вязкого трения при достаточно малых скоростях движения тела. Если тело выведено из положения равновесия на величину x и при этом имеет скорость dx/dt, то на него будут действовать квазиупругая сила –kx и сила сопротивления движению –v, где,  – коэффициент сопротивления.

Согласно второму закону динамики дифференциальное уравнение колебаний будет иметь вид

,

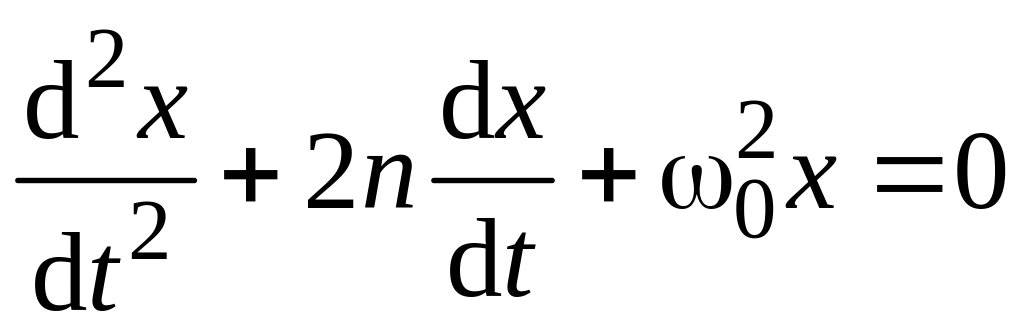где

Решение этого уравнения можно получить, исходя из следующих соображений. Во-первых, наличие квазиупругих сил свидетельствует о том, что в системе, выведенной из положения равновесия, должны возникнуть колебания. Во-вторых, наличие сил сопротивления движению приводит к тому, что энергия колебательной системы и, следовательно, амплитуда колебаний с течением времени должны уменьшаться, кроме того, сопротивление среды, тормозя движение тела, влияет на быстроту колебаний, т. е. циклическая частота колебаний может зависеть от сопротивления среды. Следовательно, решение уравнения имеет вид

.

Вынужденными называются колебания системы, возникающие под воздействием внешней силы с амплитудой . Их характер определяется как свойствами самой колебательной системы, так и внешней силой. По основному закону динамики можно составить дифференциальное уравнение движения:

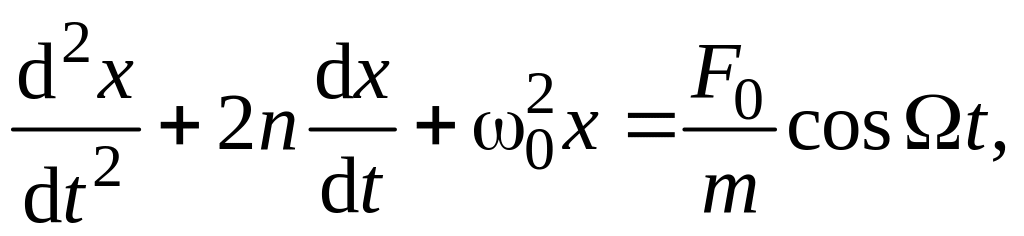
где  – циклическая частота вынуждающей силы.

Такие уравнения называются неоднородными (или уравнениями с правой частью). Как известно из теории дифференциальных уравнений, решение неоднородного уравнения можно представить в виде суммы общего решения однородного уравнения, соответствующего данному неоднородному, и какого-либо частного решения всего неоднородного уравнения в целом. Однородное уравнение, соответствующее данному неоднородному, получим, если правую часть уравнения положить равной нулю, т. е. получим дифференциальное уравнение затухающих колебаний. Что же касается частного решения всего неоднородного уравнения в целом, то оно может быть представлено гармонической функцией, изменяющейся с той же частотой, что и сама внешняя сила. При частоте вынуждающей силы, равной нулю, т. е. при действии постоянной внешней силы, тело отклоняется от положения равновесия и, когда сила упругости уравновесит внешнюю силу, движение прекратится. При бесконечно большой частоте вынуждающей силы тело, обладая массой (инертностью), не успевает получить заметное смещение за период колебаний. При промежуточных значениях частоты амплитуда отлична от нуля, следовательно, амплитуда зависит от частоты вынуждающей силы. По том же соображениям фаза колебаний тела также должна зависеть от частоты вынуждающей силы и отличаться от фазы самой силы.

Первой частью решения уравнения для однородного уравнения (затухающие колебания) через достаточно большой промежуток времени, когда прекратятся переходные процессы, можно пренебречь. Поэтому будем рассматривать только вторую часть решения, т. е. частное решение уравнения в виде гармонической функции:

.