1.2.Закон Кулона. Принцип суперпозиции электростатических полей.

1. З акон Кулона: сила взаимодействия двух точечных зарядов направлена по прямой, соединяющей эти заряды и численно равна: 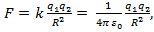где 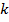– коэффициент пропорциональности, который в системе СИ равен

В векторной форме: .

Е сли заряды одноименные, то

Если заряды разноименные, то

2. Принцип суперпозиции:

Если на точечный заряд действует несколько зарядов,

то

3. Также можно получить: 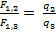. Следовательно, получим способ измерения заряда через эталонный ( .

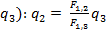2. Электрическое поле и его свойства. Напряженность. Поток вектора напряженности. Теорема Остроградского-Гаусса и примеры ее применения.

Взаимодействие зарядов происходит посредством поля.

Напряженность электрического поля – это вектор, численно равный отношению силы, действующей на положительный заряд, помещенный в данную точку поля, к заряду:

.

Размерность напряженности системе СИ: [E] = В/м.

Электрические поля подчиняются принципу суперпозиции: напряженность поля, создаваемого несколькими зарядами, равна векторной сумме напряженностей полей, создаваемых каждым зарядом в отдельности.

Силовые линии.

С иловые линии – это линии, в каждой точке которых вектор напряженности направлен по касательной.

Разноименные Одноименные

заряды: заряды:

Поток вектора напряженности. Теорема Остроградского-Гаусса.

Поток вектора через площадку dS есть скалярное произведение

где –элементарный поток, – элементарная площадка

Если площадка конечна, то .

Теорема Остроградского-Гаусса

Поток вектора напряженности электрического поля через любую замкнутую поверхность равен алгебраической сумме зарядов, находящихся внутри поверхности, деленная на электрическую постоянную

Это связь между электрическим полем и зарядами, его создающими (полем и истоком).

Данная теорема позволяет решать следующие задачи:

1. По заданной конфигурации зарядов можно определить электрическое поле.

2. По заданному электрическому полю можно найти конфигурации зарядов.

3. Это закон Кулона в полевой форме.

Рассмотрим примеры.

П ример 1: Дано тело сферической формы, заряд распределен равномерно.

Возьмем сферу радиуса и учитывая то, что нет никаких искажений получим:

То есть поле тела сферической формы, может быть рассчитано как поле точечного заряда такой же величины, помещённого в центре сферы.

Пример 2: Возьмем бесконечную равномерно заряженную плоскость, плотность заряда .

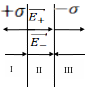
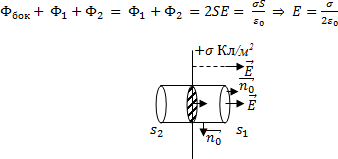
Пример 3: Изобразим силовые линии между двумя бесконечными

разноименно одинаково по модулю заряженными пластинами,

используя принцип суперпозиции. Участки I и III идентичны и на них напряженность равна нулю: . На участке II: Электрическое поле

заключено между бесконечными плоскостями.

3. Работа сил электростатического поля. Разность потенциалов и потенциал.

Связь разности потенциалов с напряженностью.

Из механики нам известна формула элементарной работы:

, где – проекция вектора

перемещения на направление вектора . (Заряд создает поле, в этом поле

перемещается положительный заряд + q.)

Отсюда получаем:

эта разность зависит только от выбора начальной и конечной точек и не зависит от формы пути.

Физическая величина, численно равная работе по перемещению единичного положительного заряда из одной точки в другую есть разность потенциалов между этими точками поля.

Т.о. можно говорить о разности потенциалов как о некоторой энергетической характеристике двух точек поля. Если одну из точек можно как-то определить, задать, то все другие точки поля будут иметь однозначные характеристики относительно этой точки.

До этого мы имели дело с интегралом: , представим теперь, что . Тогда:

Тогда получаем:

Потенциал точки численно равен работе по перемещению единичного положительного заряда из данной точки в бесконечность.

Далее рассмотрим следующее равенство: . Или:

Распишем вектора : и . Подсчитаем их скалярное произведение:

Таким образом, – градиент (векторная величина) скалярной величины . То есть: . Градиент потенциала показывает направление наибольшего возрастания скалярной величины . Тогда показывает направление наибольшего убывания потенциала .

Точки поля, в которых потенциал постоянен, образуют эквипотенциали. Силовые линии напряженности перпендикулярны эквипотенциалям. Например, в электролитической ванне можно наблюдать следующее: