3. Оценка точности косвенных измерений
При оценке точности косвенных измерений первоначально получают формулу для относительной погрешности. Для этого данную функциональную зависимость подвергают ряду операций:
1) логарифмируют;
2) дифференцируют;
3) переходят от бесконечно малых приращений dx к конечным Δx;
4) знаки минус заменяют на плюс.
В качестве примера произведем
перечисленный выше набор операций с
формулой плотности цилиндра
.
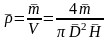1)
2)
3)
.
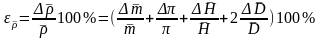Зная относительную погрешность можно найти абсолютную по формуле:
.
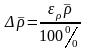4. Правила вычисления погрешностей
Погрешность обычно выражают одной значащей цифрой и лишь при особо ответственных измерениях – двумя. Погрешности измерения указывают, какие цифры являются сомнительными в числовом значении измеренной величины. Так как точность определения физической величины определяется измерением, а не вычислением, то округление числового значения результата измерения производится до цифры того же порядка, что и значение погрешности.
При округлении результатов измерений необходимо помнить следующие правила приближенных вычислений.
1. Лишние цифры у целых чисел заменяются нулями, а у десятичных дробей отбрасываются,
Например, Y= 123 357 ± 678 (до округления); Y = 123 400 ± 700 (после округления).
2. Если заменяемая нулем или отбрасываемая цифра старшего разряда меньше 5, то остающиеся цифры не изменяются, а если указанная цифра больше или равна 5, то последняя остающаяся цифра увеличивается на единицу:
Например, Y = 237,46 ± 0,13 (до округления); Y= 237,5 ± 0,1 (после округления).
При представлении окончательных результатов физических измерений часто применяют запись числовых значений в виде десятичной дроби, умноженной на необходимую степень числа десять.
Например, числа 3106; 0,0285; 0,120 записываются так: 3,106∙103; 2,85∙10-2; 1,2∙10-1. Скорость света 300 000 км/с обычно записывают как 3∙105 км/с.
5. Графическое представление результатов экспериментов
В большинстве случаев экспериментального изучения различных физических явлений целесообразно представить полученные зависимости в виде графика.
Как оценить, согласуются ли результаты опыта с ожидаемой величиной, получаемой из зависимости между измеряемыми величинами? Наглядное представление об этом получают, сопоставляя теоретическую кривую и найденные экспериментально точки. Особенно удобно проверить, ложатся ли данные точки на прямую. Поэтому при построении графиков желательно выбирать такие координаты, чтобы ожидаемая зависимость была линейной.
Например, при определении ускорения свободного падения из соотношения h= gt2/2 между высотой и временем падения удобно строить график координатах (t2, h). Тогда g= 2 tg α, т. е. определяется по всей совокупности результатов измерений t и h [по наклону прямой h(t2)].
Экспериментальные точки на графике представляют в виде крестиков, размах по высоте и ширине которых равен удвоенным погрешностям измерения, отложенных по осям величин.