Сравнение вещественных чисел.

Для любых двух вещественных чисел a и b установлено одно из отношений: (a равно b), 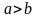или (a больше b или b больше а). Отношение = обладает свойством: если и , то .

Вместо отношения пишут также (b меньше a). Запись вида (или, что то же, ) обозначает, что либо , либо . Соотношения , , , называются неравенствами. Неравенства и называются строгими неравенствами.

Число а, удовлетворяющее неравенству , называется положительным, а число a, удовлетворяющее неравенству , – отрицательным.

Отношения >, < обладают следующими свойствами.

10. Если и , то (транзитивность).

11. Если , то 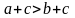(к обеим частям неравенства можно прибавлять любое число и при этом знак неравенства не изменяется).

12. Если и , то .

13.Если , то (при умножении неравенства на отрицательное число знак неравенства изменяется на противоположный) .

14. Если и , то (неравенства одного знака можно почленно складывать).

Непрерывность вещественных чисел

15. Пусть X и Y – два множества, состоящие из вещественных чисел. Тогда, если для любых чисел и выполняется неравенство , то существует хотя бы одно число c, такое, что для любых чисел x и y выполняются неравенства

.

Следует заметить, что свойством непрерывности обладает множество всех вещественных чисел, но им не обладает множество только рациональных чисел. Действительно, пусть множество X состоит из рациональных чисел x, для которых выполняется неравенство , а множество Y состоит из рациональных чисел y, для которых выполняется неравенство 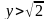. Тогда, очевидно, для любого числа и любого числа выполняется неравенство . Однако, не существует рационального числа c такого, чтобы выполнялись неравенства . В самом деле, таким числом могло бы быть только , которое, но оно не является рациональным.

Теперь окончательно будем считать, что вещественные числа представляют собой множество элементов, обладающих свойствами 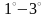. Такое определение вещественных чисел называется аксиоматическим, а свойства аксиомами вещественных чисел.

В дальнейшем будем иметь дело с различными множествами вещественных чисел. Всюду, где это не может привести к неточности, для краткости вещественные числа будем называть просто числами.

Если – произвольные числа, то запись означает, что число x максимальное (минимальное) из чисел .

Установим взаимно-однозначное соответствие между точками бесконечной направленной прямой и множеством вещественных чисел. Пусть , где

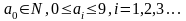.Рассмотрим направленную прямую, на которой указаны две точки О и Е. Точка О – начало отчета, отрезок ОЕ – масштабный отрезок. Точке О поставим в соответствии число , которое называется нулем.

а) Сначала произвольной точке М поставим в соответствии определенное вещественное число, указав каким образом будет выписываться (строиться) бесконечная десятичная дробь которая соответствует точке М.

Пусть точка Е лежит справа от 0. Будем рассматривать точку М, лежащую лишь справа от точки О, т.к. точкам, которые лежат слева будут соответствовать отрицательные вещественные числа, десятичные знаки которых определены так же, как и для точек справа от О.

Число a₀ положим равным максимальному числу отрезков ОЕ, которые укладываются внутри отрезка ОМ. Если остатка не получается, то полагаем Если отрезок ОЕ укладывается внутри отрезка OM и остается отрезок меньший, чем ОЕ, то цифру , выбираем как наибольшее число отрезков , целиком укладывающихся внутри .

Если после этого не получается остатка, то полагаем Если получается остаток 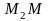, то цифру находим, сравнивая длину отрезка с отрезком 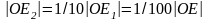. Продолжая этот процесс, получим бесконечную десятичную дробь , соответствующую точке М.

Таким образом, любой произвольной точке численной прямой поставлено в соответствие вещественное число х. Легко проверить, что двум различным точкам прямой будут соответствовать два различных числа или две различные десятичные дроби.

б) Теперь покажем обратное, что любому вещественному числу соответствует некоторая точка М направленной прямой. Воспользуемся аксиомой Кантора: для любой последовательности вложенных отрезков :

на прямой существует хотя бы одна точка М, принадлежащая всем отрезкам .

Пусть произвольное положительное вещественное число, а и две конечные десятичные дроби, т.е. два рациональных числа, удовлетворяющих неравенству: . Числа называются нижним и верхним n-значными приближениями числа x.

Рациональное число соответствует точке прямой ОЕ, которое определяется следующим условием:

.

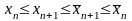Точно также рациональное число соответствующее точке .Т.к. , то отрезки вложены друг в друга. В силу аксиомы Кантора существует точка М, которая принадлежит всем отрезкам одновременно. В силу построенного выше соответствия образом точки М будет вещественное число .

Следовательно, построено взаимно однозначное соответствие между множеством действительных чисел и множеством точек на прямой линии. Прямая линия, на которой откладываются вещественные числа, называется числовой прямой. Ясно, что точке О соответствует число 0, а точке Е – число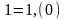 .