
- •Глава 2. Числовые последовательности
- •2.1. Сходящиеся числовые последовательности
- •2.2.Арифметические свойства сходящихся последовательностей
- •Определение 8. Последовательность называется бесконечно большой, если
- •В этом случае, если , то пишут , если или , то пишут .
- •В заключение докажем теорему, которая определяет число e, играющее очень важную роль в математике. Теорема 8. Последовательность имеет предел.
- •Следуя Эйлеру, предел этой последовательности обозначают через e. Таким образом, записывают:
- •2.3. Теорема Больцано-Вейерштрасса. Фундаментальные последовательности
- •2.4. Числовые ряды.
- •2.5. Контрольные вопросы.
- •26. Числовые ряды
- •2.6. Примеры решения задач
- •2.7. Задачи для самостоятельного решения
2.7. Задачи для самостоятельного решения
Написать пять первых элементов каждой из последовательностей, заданных их общими элементами:
1. .
2.
.
2. .
.
3.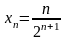 .
4.
.
4. .
.
Зная несколько первых элементов последовательности, написать формулу общего элемента таких последовательностей:
5.
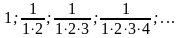 6.
6.
 …
7.
2; 10; 26; 82; 242; 730; ...
…
7.
2; 10; 26; 82; 242; 730; ...
Написать пять первых элементов последовательности, используя формулу общего элемента этой последовательности:
8. 9.
9.
Ограничены ли последовательности:
10. .
11.
.
11.
 .
.
12.
 . 13.
. 13.
 .
.
14. 1, 0, 2, 0, 3, 0, 4, 0, 5, ...
Пользуясь определением, доказать, что последовательности являются бесконечно большими:
15. .
16.
.
16. .
.
17.
 . 18.
. 18.
Используя определением, доказать, являются ли бесконечно малыми такие последовательности:
19.
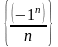 . 20.
. 20.

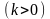 .
.
21. .
22.
.
22.
23.
Показать, что частное двух бесконечно
больших последовательностей
 и
и
 может быть любой последовательностью,
используя в качестве примеров
последовательности
может быть любой последовательностью,
используя в качестве примеров
последовательности
 и
и
 .
.
24.
Докажите, что если
 – бесконечно малая последовательность,
– бесконечно малая последовательность,
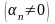 ,
то
,
то
 – бесконечно большая последовательность.
– бесконечно большая последовательность.
25.
Покажите, что неограниченная
последовательность
 не является бесконечно большой.
не является бесконечно большой.
26.
Докажите, что последовательность
 имеет своим пределом число 2.
имеет своим пределом число 2.
27.
Докажите, что последовательность
 имеет своим пределом число 0.
имеет своим пределом число 0.
Используя определение предела, докажите, что:
28.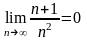 . 29.
. 29. .
.
30. .
31.
.
31. .
.
(Указание:
представить выражение общего элемента
последовательности в виде
 или
или
 .)
.)
32.
 33.
33.
 34.
34.
 .
.
35.
Докажите, что если
 ,
то
,
то
 .
.
36.
Известно, что последовательность
бесконечно большая, а последовательность
имеет конечный предел
 .
Что можно сказать о последовательности
.
Что можно сказать о последовательности
 ?
?
37.
Известно, что
 .
Найдите номер
,
начиная, с которого выполняется
неравенство
.
Найдите номер
,
начиная, с которого выполняется
неравенство
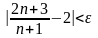 ,
где
,
где
 .
.
Приведите
примеры таких последовательностей:
и
,
что
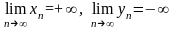 ,
кроме того:
,
кроме того:
38.
 .
39.
.
39.
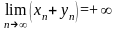
40.
 41.
41.
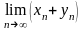 не существует.
не существует.
Приведите
примеры таких последовательностей
и
,
чтобы
,
 и, кроме того:
и, кроме того:
42.
 . 43.
. 43. .
.
44. 45.
45.
 не существует.
не существует.
46.
Известно, что последовательности
и
расходятся. Могут ли последовательности
,
быть сходящимися? расходящимися? Ответы
обоснуйте примерами последовательностей
 .
.
47.Докажите,
что (
– любое число).
(
– любое число).
48.Докажите,
что последовательность с общим элементом
 сходится
и найдите ее предел.
сходится
и найдите ее предел.
49.Последовательность
задана рекуррентным соотношением
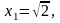
 .
Докажите, что эта последовательность
сходится, и найдите ее предел.
.
Докажите, что эта последовательность
сходится, и найдите ее предел.
Найти пределы:
50.
 . 51.
. 51.
 .
.
52. . 53.
. 53. .
.
54.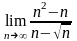 . 55.
. 55. .
.
56. .
57.
.
57. .
.
58. 59.
59.
60. . 61.
. 61.
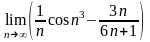 .
.
62. . 63.
. 63. .
.
64.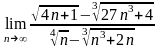 . 65.
. 65. .
.
66. 67.
67.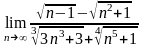
68. 69.
69.
70. 71.
71.
72. 73.
73.
74. 75.
75.

