Определение 8. Последовательность называется бесконечно большой, если

.

В этом случае, если , то пишут , если или , то пишут .

Теорема 7. а) Если и 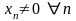, то последовательность – бесконечно малая;

б) если , то последовательность - бесконечно большая.

□ а) Пусть . Тогда для последовательности имеем: , т. е. – бесконечно малая.

б) Доказать самостоятельно. ■

В заключение докажем теорему, которая определяет число e, играющее очень важную роль в математике. Теорема 8. Последовательность имеет предел.

□ Сначала заметим, что при выполняется неравенство

или . (3)

Воспользуемся формулой бинома Ньютона:

При а=1, b=1/n получим:

Последовательность с ростом n возрастает, т.к. увеличивается каждый член суммы, а число членов всякий раз увеличивается на единицу, т.е. не убывает и ограничена. Тогда по теореме 3последовательность сходится.

■

Следуя Эйлеру, предел этой последовательности обозначают через e. Таким образом, записывают:

Известно, что (способ вычисления покажем в дальнейшем): e= 2,71828 …

Постоянное число e называют числом Д.Непера (1550-1617). Логарифм числа а по основанию e называется натуральным логарифмом числа а и обозначается символом a.

2.3. Теорема Больцано-Вейерштрасса. Фундаментальные последовательности

Больцано Бернар ( 1781-1848), Вейерштрасс Карл (1815-1897).

Определение 9. Пусть - числовая последовательность и - возрастающая последовательность натуральных чисел. Последовательность называется подпоследовательностью последовательности .

Если подпоследовательность сходится, то ее предел называется частичным пределом последовательности . Например, последовательность не сходится, т.е. расходится. Ее подпоследовательность расходится, а сходится.

Теорема 9. Если последовательность сходится, то любая ее подпоследовательность также сходится и имеет тот же предел.

□ Пусть и , тогда . Очевидно, . Это значит, что . ■

Теорема 10 (о вложенных отрезках). Пусть - последовательность вложенных отрезков, т.е. , и или . Тогда существует по меньшей мере одна точка, принадлежащая всем отрезкам одновременно.

□ По условию последовательность не убывает, а не возрастает. Также по условию и ограничены, т.к. . Тогда по теореме 3существуют и . Причем (по теореме сравнения).Очевидно, что . Т.о., точки и принадлежат всем вложенным отрезкам (они могут и совпадать). ■

Теорема 11 (Больцано - Вейерштрасс). Из всякой ограниченной можно выделить сходящуюся подпоследовательность.

□ Пусть последовательность ограничена. Это означает, что , т.е. все значения лежат на отрезке 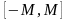.Обозначим для удобства этот отрезок как . Разделим его пополам. По крайней мере, один из полученных отрезков содержит бесконечное число членов последовательности (или оба).

Выберем ту часть отрезка , где - бесконечное множество, и обозначим ее через . Отрезок снова делим пополам и выбираем ту половину, где членов числовой последовательности бесконечно много и обозначаем ее и т.д. Получим последовательность вложенных отрезков. Причем длина отрезков равна:

, .

В силу теоремы 10, существует точка с, которая принадлежит всем отрезкам:

(4)

Построим подпоследовательность сходящуюся к числу с. В качестве 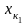возьмем любой член последовательности . В качестве возьмем элемент последовательности , лежащий на , у которого (т.к. на членов последовательности бесконечно много, то так всегда можно выбрать). В качестве возьмем элемент последовательности из отрезка 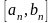, у которого :

(5)

Покажем, что . Действительно, из (4) и (5) и геометрических соображений следуют неравенства . Переходя к пределу, получим . ■

В качестве иллюстрации к этой теореме можно взять ограниченную последовательность , которая расходится. Её подпоследовательность - сходится.

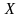Пусть - ограниченная последовательность: . Обозначим через множество частичных пределов последовательности . Ясно, что (по теореме 10).Очевидно, что ограничено, т.к. если , то из неравенства Поскольку - ограниченное множество, то и Обозначим ,

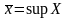Теорема 12. Числа , являются частичными пределами последовательности , т.е. , (без доказательства).

Определение 10. Числа и называются соответственно верхним и нижним пределами последовательности и обозначаются:

, .

Пример. Последовательность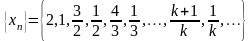 имеет верхний и нижний пределы , .

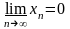Определение сходимости последовательности связано с пределом этой последовательности, который заранее неизвестен, т.е. трудно непосредственно проверять сходимость. Поэтому желательно использовать для этого некоторые “внутренние свойства” последовательностей.

Определение 11. Последовательность называется фундаментальной, если

.

Ясно, что члены фундаментальной последовательности с увеличением номера сближаются между собой.

Теорема 13. Если последовательность фундаментальная, то она ограничена.

□ Фиксируем .Тогда . Возьмем , тогда и

.

Т.е. все члены при 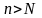ограничены числом .

Положим . Очевидно, , т.е. по определению последовательность ограничена. ■

Теорема 14 (критерий Коши,1789-1857). Для того чтобы последовательность была сходящейся, необходимо и достаточно, чтобы она была фундаментальной.

□ а) Необходимость. Пусть сходится, - предел. Докажем, что она фундаментальная. По определению имеем:

.

Тогда

,

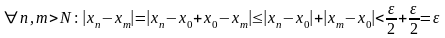т.е. - фундаментальная.

б) Достаточность. Пусть - фундаментальная последовательность. Докажем, что она сходится.

Последовательность ограничена (теорема 13).Следовательно, можно выделить подпоследовательность , сходящуюся к некоторому числу .Покажем, что и сходится к .Пусть - произвольное положительное число. По условию теоремы, т.к. последовательность фундаментальная, то

и .

Поскольку , то из последнего неравенства при получим 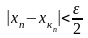при . Подпоследовательность сходится, поэтому существует такой , что при выполняются неравенства: .Пусть , тогда при :

Это означает, что последовательность сходится к . ■

Пример. Доказать, что последовательность ,

где - произвольные вещественные числа, удовлетворяющие условию , , 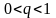сходится.

Решение. Пусть и 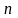- любые натуральные числа. Обозначим .

Учитывая, что последовательность - бесконечно малая, т.е. , получим, что при .