2. Однородные дифференциальные уравнения первого порядка

Функция f (x, y) называется однородной функцией m-го измерения, если f (λx, λy) = λ^m f (x, y).

Дифференциальное уравнение вида

P(x, y) dx + Q(x, y) dy = 0, (5)

где P(x, y) и Q(x, y) – однородные функции одинакового измерения, называется однородным дифференциальным уравнением первого порядка.

Практическое правило: если суммы показателей степеней всех переменных в каждом из слагаемых равны, то функция – однородная.

Примеры. 3х² + 2ху – у², – однородные функции степени 2 и 0 соответственно;

5х² – 3у² + 1, 5х² + 2х – 3у² – не однородные функции.

Уравнение (5) можно привести к виду y’ = f , где f – однородная функции нулевого измерения.

Однородное уравнение преобразуется в уравнение с разделяющимися переменными при помощи замены переменной = u, т.е. y = ux, где u = u (х) – новая неизвестная функция.

Имеем y = ux, y′ = u′x + u.

Подставляя эти выражения вместо у и у в исходное уравнение, получим уравнение с разделяющимися переменными относительно переменной u. Решив его, окончательно получим решение в виде зависимости у от х: y = ux.

Замечание 1. Вместо подстановки 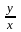= u можно применять подстановку = u.

ЗАДАЧИ

1. Решить дифференциальные уравнения. Найти частное решение (интеграл), если указаны начальные условия:

   1. y’ = .

Р е ш е н и е. Т.к. = , то y’ = является однородным уравнением. Имеем:

y’ = => y’ = => || = u => y = ux, y’ = u + u’x || => u + u’x = => u’x = – u =>

=> u’x = => u’x = => x = = 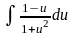=> arctg u – ln(1 + u²) = ln | x | + C.

Сделав обратную замену u = , получим общий интеграл arctg – ln (1 + u²) = ln | x | + C.

2. (x + 2y) dx – x dy = 0.

3. y² + x² y’ = xyy’.

4. y’ = – .

5. xy’ = y – x .

6. (x² + y²) dx – 2xy dy = 0, y(0) = 4.

7. (x² – 3y²) dx + 2xy dy = 0, y(2) = 1.

Замечание 2. Уравнение вида 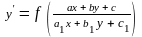приводится к однородному или с

разделяющимися переменными. Для этого вводят новые переменные u и v, положив

х = u + α, у = v + β, где α и β – числа. Их подбирают так, чтобы уравнение стало однородным.

Если = , то исходное уравнение приводится к уравнению с разделяющимися переменными

подстановкой u = ax + by.

3. Линейные уравнения первого порядка

Линейным дифференциальным уравнением первого порядка называется уравнение вида

a₁(x) y’ + a₀(x) y = b(x) или

y’ + p(x) y = q(x). (6)

Замечание. Уравнение вида х + p(y) x = q(y) является линейным относительно х и х.

Если q(x)  0, то уравнение (1) принимает вид у + р(х) у = 0, и называется линейным однородным. Оно является уравнением с разделяющимися переменными. В случае q(x)  0 уравнение (1) называется линейным неоднородным уравнением.

Основным методом решения линейного дифференциального уравнением первого порядка является метод Бернулли или, как его часто называют, метод «u на v», состоящий в том, что решение ищется в виде произведения двух функций

y = uv, (7)

где u = u(x), v = v(x) – неизвестные функции от х, причем одна из них c точностью до константы произвольна (но не равна тождественно нулю). При подстановке (7) уравнение (6) примет вид

u’v + uv’ + p(x) uv = q(x) или [u’ + p(x)u]v + v’u = q(x). (8)

Если потребовать, чтобы выражение в квадратных скобках было равно нулю, т.е.

u’ + p(x)u = 0, (9)

то из (9) найдем u(x), затем из (8) найдем v(x), а, следовательно, из (7) найдем у.

Пример 1. Решить методом «u на v» дифференциальное уравнение y’ – y = 2x³.

Р е ш е н и е. y = uv => y’ = u’v + uv’ => u’v + uv’ – uv = 2x³ =>

• v[u’ – u] + uv’ = 2x³ .

1. u’ – u = 0 => = => = 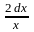ln|u| = 2ln|x| => u = x² .

2. uv’ = 2x³ => x²v’ = 2x³ => = 2x v = x² + C .

3. y = uv => y = x² (x² + C).

Другой метод решения линейных уравнений – это метод вариации произвольной постоянной (метод Лагранжа). Сначала решается уравнение

y’ + p(x) y = 0,

которое получается из уравнения (6), если приравнять его правую часть нулю. Это уравнение с разделяющимися переменными. Решим его и в полученном решении заменим константу С переменной С(х).

Решая полученное таким образом дифференциальное уравнение, получим окончательный ответ.

Пример 2. Решить методом вариации произвольной постоянной диф. уравнение y’ – y = 2x³.

Р е ш е н и е.

1) y’ – y = 0 => = => = ln|y| = 2ln|x| + ln|C| => y = Cx² .

2) y = C(x) x² => y’ = C’x² + 2Cx => C’x² + 2Cx – Cx² = 2x³ => C’x² = 2x³ => C’ = 2x C(x) = x² + C .

3. y = C(x) x² => y = (x² + C) x².

ЗАДАЧИ

1. Решить дифференциальные уравнения методом «u на v» . Найти частное решение (интеграл), если указаны начальные условия:

1. y’ + y tg x = .

2. x² y’ + xy + 1 = 0.

3. y = x (y’ – x cos x).

4. (2x + 1) y’ = 4x + 2y.

5. y’ – – 1 – x = 0, y(0) = 0.

6. x y’ + y – e^x = 0, y(a) = b.