Модификаторы

Модификатор	Положение	Назначение
DISTINCT	после слова SELECT	гарантирует уникальность решений (исключает дублирование результатов)
REDUCED	после слова SELECT	предписывает выдачу всех решений, включая повторы
ORDER BY	после раздела WHERE {}	сортировка решений (результатов)
OFFSET <n>	после раздела WHERE {}	предписывает исключить из выборки n первых решений
LIMIT <n>	после раздела WHERE {}	ограничивает количество выдаваемых решений

Выполнение запросов осуществляется на вкладке «SPARQL Query» (рис. 24).

Запрос

Префикс онтологии

Результаты запроса

Запуск запроса на выполнение

Рис. 24. Вкладка «SPARQL Query»

Перед выполнением запросов рекомендуется указать сокращенное имя (префикс) онтологии, чтобы в дальнейшем не было необходимости указания полного IRI для ее элементов (классы, свойства, индивиды).

На рис. 24 показан стандартный запрос, отображаемый при первом открытии данной вкладки. Он предписывает вывести все подклассы (переменная ?subject) для всех классов (переменная ?object), определенных в онтологии.

Ниже приводятся несколько запросов с использованием модификаторов и графовых шаблонов (рис. 25, 26).

Показать фамилию, имя и группу 3 студентов (LIMIT 3), пропустив первых 2 (OFFSET 2), в виде отсортированного списка по фамилии (ORDER BY ASC(?fam)).

Показать фамилию, имя и номер квартиры студентов, у которых этот номер меньше 40 (FILTER (?number < 40)).

Рис. 25. Запрос с модификаторами

Рис. 26. Запрос с графовым шаблоном

Задание на выполнение работы

А. Протестировать в Protégé с помощью SPARQL-запросов онтологическую модель, разработанную по варианту, выбранному в лабораторной работе № 4.

Б. Отчет должен содержать:

• титульный лист;

• описание задания;

• копии экранов программы с 5–7 SPARQL-запросами, содержащими модификаторы и графовые шаблоны;

• вывод.

Контрольные вопросы

1. Дайте определение понятия «онтология».

2. Перечислите основные языки онтологического представления знаний.

3. Перечислите основные составляющие (типы элементов) онтологии.

4. Опишите структуру URI(IRI).

5. Перечислите нотации для описания онтологий RDF/RDFS и OWL.

6. Дайте характеристику RDF-тройки.

7. Назовите основные отличия представления предметной области с помощью онтологий RDF/RDFS и языков объектно-ориентированного программирования.

8. В чем заключается отличие свойств-отношений от свойств-данных в RDF/RDFS?

9. Для чего используется SPARQL?

10. Перечислите основные элементы (разделы) SPARQL-запроса.

3. Эвристические алгоритмы

3.1. Методы поиска решений с использованием графов

При решении логических или оптимизационных задач пространство поиска часто представляется в виде графа – упорядоченной пары непустых множеств вершин (узлов) и ребер (дуг). Одной из разновидностей графа является дерево – связный ациклический граф. Связность означает наличие путей между любой парой вершин, ацикличность – отсутствие циклов.

Ниже рассматриваются некоторые популярные методы поиска решений с использованием графов. Процедура поиска этих методов заключается в обходе дерева и исследовании его узлов (проверке частичных или полных решений) на предмет удовлетворения условиям задачи и/или оптимальности.

1. Метод перебора с возвратами (решение логических задач)

Наиболее известным и часто используемым, в том числе и на бытовом уровне, способом решения задач является метод перебора с возвратами, называемый также методом проб и ошибок. При научном подходе использование метода позволяет найти точное решение задачи.

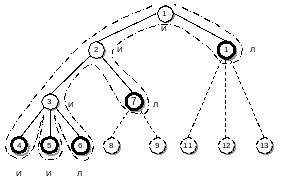
Рис. 27. Обход дерева при поиске решения: – направление поиска для узлов, решение в которых удовлетворяет условиям; – направление поиска для узлов, решение в которых не удовлетворяет условиям; – маршрут обхода узлов; – узел, в котором решение удовлетворяет условиям задачи; – узел, в котором решение не удовлетворяет условиям задачи; – узел с итоговым решением задачи; – узел, не попавший в маршрут обхода.

Все пространство поиска можно представить в виде дерева, узлами которого являются частичные или итоговые решения задачи (необязательно верные). По мере поиска решения, удовлетворяющего условиям (требованиям, ограничениям), постепенно строится это дерево (выполняется обход узлов). Если в листьях (узлах последнего уровня) решение удовлетворяет требуемым условиям, то оно и есть результат поиска. В общем случае решений может быть несколько (см. рис. 27 узлы 4 и 5). Если при обходе дерева попадается узел, решение в котором не удовлетворяет (противоречит) условиям задачи, тогда выполняется возврат к предыдущему узлу верхнего уровня и продолжается поиск в альтернативном направлении. В частном случае обход дерева может быть прерван при нахождении первого верного решения.

Такой способ поиска решения при обходе дерева сверху вниз слева направо называется поиском в глубину. Он используется в языке программирования Пролог при автоматическом поиске ответа на вопрос.

Ограничением использования метода является монотонность выводов. То есть если в каком-либо узле проверяемое условие ложно, то в узле следующего уровня оно не может стать истинным и наоборот. Очевидно, что при большом количестве проверяемых условий и направлений поиска данный метод малоэффективен.

2. Метод частичного перебора (точный метод решения оптимизационных задач) [3].

При решении оптимизационных задач широко используются методы математического программирования. Одним из них является метод частичного (неявного) перебора, называемый также методом ветвей и границ. При обходе дерева (рис. 28) в узлах помимо проверки допустимости (соответствия ограничениям) считается и проверяется значение выбранного критерия (целевой функции). Если значение этого критерия (при минимизации целевой функции) в текущем узле больше, чем значение, полученное в ранее пройденном и удовлетворяющем всем условиям узле, то дальнейший поиск из текущего узла не ведется (так как значение критерия в узлах ветвей, исходящих из него, не будет лучше).

Рис. 28. Обход дерева при поиске решения методом частичного перебора (К_п – значение критерия в промежуточном узле; К_и – значение критерия в узле, соответствующем полному набору ограничений)

Оптимальным решением в рассмотренном примере является решение в узле 5. Поиск решения из узла 7 не выполнялся, так как решения в узлах 8 и 9 дадут заведомо худший результат по сравнению с решением в узле 5.

Ограничением использования этого метода является как монотонность выводов, так и монотонность критерия (целевой функции). То есть значение критерия в узле, из которого ведется поиск, не может быть больше значения критерия в нижележащих узлах. В случаях, когда надо максимизировать целевую функцию, считают величину, обратную критерию 1/К.

3. Алгоритм А* (эвристический метод решения оптимизационных задач) [1].

Эвристический алгоритм (метод) – алгоритм, не гарантирующий нахождения точного или оптимального решения поставленной задачи, но дающий достаточно хороший результат в большинстве случаев.

Эвристические алгоритмы используются в тех случаях, когда точные методы не позволяют найти решение задачи за приемлемое время. Одним из таких методов является алгоритм А*.

В нем для всех узлов, удовлетворяющих ограничениям и в которые можно попасть из корневого узла, вычисляется значение критерия. Дальнейший процесс поиска выполняется только из узла, в котором значение критерия максимально (минимально), остальные ветви поиска не рассматриваются (рис. 29).

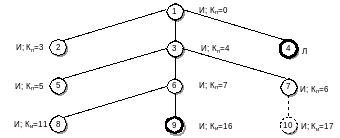
Рис. 29. Поиск решения с помощью алгоритма А*

Недостатком данного алгоритма является возможный пропуск оптимального решения (см. рис. 29 узел 10), но найденное итоговое решение очень часто является оптимальным или, по крайней мере, достаточно хорошим (эффективным).

В табл. 8 приведена сравнительная характеристика рассмотренных выше методов решения оптимизационных задач.

Таблица 8