Свойства функций, непрерывных на отрезке
1. Если функция
непрерывна на отрезке
,
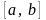то она ограничена на этом отрезке.
2.
Если функция
непрерывна на отрезке
,
то она достигает на этом отрезке
наименьшего значения m
и наибольшего значения M
(т.е. существуют на этом отрезке точка
,
в которой
,
и точка
,
в которой
).
3.
Если функция
непрерывна на отрезке
и ее значения на концах отрезка имеют
разные знаки*,
то внутри отрезка найдется такая точка
c, что
.
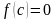Эти свойства также являются теоремами. Доказать их непросто, и мы этого делать не будем.
Однако все они являются частными случаями следующего утверждения (которое интуитивно кажется очевидным):
если функция непрерывна на отрезке , то область ее изменения есть отрезок.
Решение задач
1)
;
2)
;
3)
;
4)
;
здесь теорема о пределе частного неприменима: и числитель, и знаменатель стремятся к нулю. Предел находят путем разложения числителя и знаменателя на множители:
.
(Здесь мы сократили дробь на множитель
,
который хотя и является бесконечно
малой величиной при
,
но все же отличен от нуля:
,
но
.)
5)
;
делим числитель и знаменатель на
и учитываем, что
:
;
6)
;
7)
;
умножим числитель и знаменатель на
:
;
8)
;
9)
;
10)
;
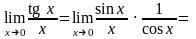
11)
;
12)
;
13)
;
Можно иначе:
.
Лекция 3. Основы дифференциального исчисления
3.1. Производная
Пусть функция
определена на некотором промежутке X.
Придадим значению аргумента
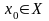произвольное приращение
так, чтобы точка
также принадлежала X.
Тогда функция
получит соответствующее приращение
.
Определение. Производной функции в точке называется предел отношения приращения функции в этой точке к приращению аргумента при (если этот предел существует):
.
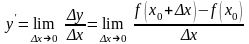Производная
имеет несколько обозначений:
,
,
.
Иногда в обозначении производной
используется индекс, указывающий по
какой переменной взята производная,
например,
.
Если функция в точке имеет конечную производную, то функция называется дифференцируемой в этой точке. Нахождение производной называется дифференцированием.
Функция, дифференцируемая во всех точках промежутка X, называется дифференцируемой на этом промежутке. В этом случае также является функцией от аргумента x, определенной на этом промежутке.
Геометрический смысл производной
Дадим определение касательной к графику функции в данной точке.
|
Рис. 1 |
Касательной к графику функции в точке M называется предельное положение секущей MN, когда точка N стремится к точке M по кривой (см. рис. 1).
Пусть точка M на кривой соответствует значению аргумента , а точка N – значение аргумента из треугольника MNA:
.
Пусть . Тогда точка N будет перемещаться вдоль кривой и в пределе совпадет с точкой M. При этом
.
Если производная в точке существует, то, согласно определению производной, получаем
.
Итак, производная
равна тангенсу угла наклона (угловому
коэффициенту) касательной к графику
функции
в точке
.
Скорость протекания физических, химических и других процессов также выражается при помощи производной.
Мгновенная скорость
Пусть функция
описывает закон движения материальной
точки по прямой (как зависимость пути
s от времени t).
Тогда за промежуток времени
пройденный путь равен
.
Отношение
есть средняя скорость за время
.
А тогда
есть мгновенная скорость в момент времени t. Итак, мгновенная скорость есть производная пути по времени.
Пример. Пусть x –
количество вещества, образовавшегося
при химической реакции к моменту времени
t. Очевидно, x
есть функция времени:
.
Если t получает
приращение
,
то x получает
соответствующее приращение
.
Тогда отношение
представляет собой среднюю скорость
химической реакции за время с момента
t до момента
,
а предел этого отношения при
,
т.е.
– скорость химической реакции в момент
t.