1.4. Элементарные функции. Основные элементарные функции.
Перечислим основные элементарные функции и напомним их наиболее важные свойства.
Степенная
функция
,
а
– действительное число.
1) a – натуральное число. Функция определена на всей числовой прямой. Функция является нечетной при a нечетном и четной – при a четном.
Если
a – нечетное, то функция
возрастает на
;
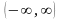если a – четное, то
убывает на
и возрастает на
;
2) a – целое отрицательное число. В этом случае функция определена при всех значениях x, кроме x = 0;
3)
.
Если n – четное, то
функция определена на
.
На
рис. 1–4 изображены графики степенной
функции соответственно при a
= 1, 2, 3, –1,
.
|
|
Рис. 1 |
Рис. 2 |
|
|
Рис. 3 |
|
|
|
Рис. 4 |
|
Степенная функция не является периодической ни при каком a.
Показательная функция
;
a > 0, a
1.
Эта
функция определена при всех значениях
.
Ее область изменения есть
.
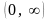Функция общего вида. Если
,
то функция всюду возрастает; если
,
то убывает. Показательная функция не
является периодической. График ее имеет
вид, изображенный на рис. 5 (при a
= 2, 3,
,
).
|
Рис. 5 |
Логарифмическая
функция
;
,
.
Эта
функция определена при
.
Ее область изменения – вся числовая
прямая
.
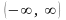Функция общего вида. Если
,
то она возрастает на
;
если
,
то убывает. График логарифмической
функции изображен на рис. 6.
|
|
а) |
б) |
Рис. 6
Тригонометрические функции*
1. Синус. .
Эта
функция определена на
.
Ее область изменения есть
.
Синус – нечетная функция. Возрастает
на
,
убывает на
,
.
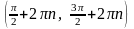Является периодической функцией с
периодом
.
График см. на рис. 7.
|
Рис. 7 |
2. Косинус.
.
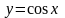Область
определения –
.
Область изменения –
.
Функция четная. Возрастает на
,
убывает на
,
.
Период
.
График см. на рис. 8.
|
Рис. 8 |
3. Тангенс.
.
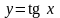Область
определения –
,
.
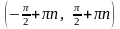Область изменения –
.
Функция нечетная. Возрастает всюду на
,
.
Период
.
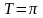График см. на рис. 9.
|
Рис. 9 |
4.
Котангенс.
.
Область
определения –
,
.
Область изменения –
.
Функция нечетная. Убывает на
,
.
Период
.
График см. на рис. 10.
|
Рис. 10 |
Обратные
тригонометрические функции:
,
,
,
.
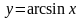Сложная
функция. Если y есть
функция от u, переменная
u есть функция от x,
т.е.
,
,
то y называется функцией
от функции, или сложной функцией:
.
Примеры:
,
.
Определение. Элементарной функцией называется функция, которая получены из основных элементарных функций и констант при помощи конечного числа операций сложения, вычитания, умножения, деления и взятия функции от функции.
Алгебраические и трансцендентные функции. К алгебраическим функциям относятся:
а) многочлены
,
в частности, линейная функция
и квадратичная функция
;
б) дробно-рациональные функции
,
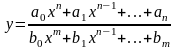т.е. функции, определяемые как отношение двух многочленов;
в)
иррациональные функции, т.е. функции
,
где наряду с операциями сложения,
вычитания, умножения и деления производятся
также операции возведения в степень с
дробными рациональными показателями,
например,
,
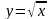и т.п.
Вообще, алгебраической функцией называется функция , которая удовлетворяет уравнению вида
,
где
,
,
...,
– многочлены, зависящие от x.
Функция, которая не является алгебраической, называется трансцендентной. Показательная, логарифмическая, тригонометрические функции являются трансцендентными.