5.1. Непрерывность

Понятие непрерывности функции нескольких переменных определяется так же, как и для функции одной переменной.

Пусть , пусть – некоторая точка. Придадим аргументам x и y приращения x, y (т.е. перейдем от к ). Тогда функция получит приращение z. Если

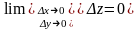, (1)

то говорят, что функция непрерывна в точке . Иначе говоря, функция непрерывна, если бесконечно малым приращениям аргументов соответствует бесконечно малое приращение функции^*.

Если учесть, что

,

и положить 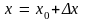, , то равенство (1) можно переписать в виде

. (2)

Равенство (2) дает нам еще одно определение непрерывности: функция непрерывна, если ее предел равен ее значению от пределов аргументов.

5.2. Частные производные

Пусть . Зафиксируем точку и, не меняя значения придадим аргументу x приращение x, т.е. перейдем от к . Если существует предел

,

то этот предел называется частной производной функции в точке и обозначается одним из символов

, , , .

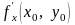Аналогично определяется частная производная по y:

.

Таким образом, частная производная функции двух аргументов по одному из аргументов – это обычная производная той функции одного аргумента, которая получается из данной функции при фиксированном другом аргументе. (Поэтому, вычисляя, например, , мы обращаемся с аргументом y как с константой.)

Примеры. 1) .

, ;

2) .

, .

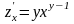5.3. Полное приращение и полный дифференциал

Полным приращением функции в точке называется разность

. (1)

Определение 1. Функция называется дифференцируемой в точке , если ее полное приращение в этой точке можно представить в виде

, (2)

где A, B – некоторые числа, а величины  и  – бесконечно малые при , .

Если хотя бы одно из чисел A и B отлично от нуля, то сумма

(3)

есть главная часть приращения z.

Определение 2. Дифференциалом функции в точке M называется главная линейная часть приращения этой функции в этой точке.

Дифференциал обозначается одним из символов: dz или . Таким образом,

. (4)

Можно доказать, что если функция имеет непрерывные частные производные, то она дифференцируема, т.е. ее полное приращение имеет вид (2), при этом 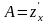, 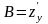. Следовательно, дифференциал имеет вид

. (5)

Можно доказать (так же, как мы это делали для функции одного аргумента), что приращения независимых аргументов совпадают с их дифференциалами: 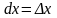, . Поэтому

, (6)

или, в других обозначениях,

. (6')

Наконец, можно доказать, что дифференцируемая функция непрерывна.

5.4. Частные производные различных порядков

Пусть дана функция . Частные производные 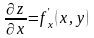и также являются функциями аргументов x и y. Поэтому от них можно снова находить частные производные. Это будут вторые частные производные:

(обозначаются также символами и ),

(обозначаются также символами и ),

(обозначаются также символами и ),

(обозначаются также символами и ).

Примеры.

1) .

, ;

, , , ;

2) .

, ;

, ;

, ;

3) .

, ;

, ;

, .

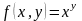Заметим, что вторые производные и (или, что то же самое, и называются смешанными. Мы видели во всех трех примерах, что (соответственно ). Это совпадение не случайно. Справедлива теорема: Если функция и ее производные , , , непрерывны в данной точке и некоторой ее окрестности, то в этой точке

.

Аналогично определяются частные производные более высоких порядков: 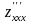, и т.д.

Можно определить также дифференциалы второго, третьего и т.д. порядков: , , ...