17. Схемы вычисления свертки и корреляции на основе бпф.

С использованием БПФ схема вычислений корреляции будет иметь вид рис.2.1.

Рис. 2.1. Схема вычисления корреляции

В свою очередь, схему вычисления свертки можно представить как показано на рис.2.2.

Рис. 2.2. Схема вычисления свертки

18. Двумерное дпф и бпф

Любой периодический сигнал может быть представлен в виде ряда Фурье, но, в отличие от одномерных сигналов, двумерные описываются двумерным рядом Фурье, имеющим вид:

.  (3.22)

Базисные функции этого двумерного представления - двумерные комплексные экспоненты (иногда называемые комплексными синусоидами)

(3.23)

имеющие, как и сигнал , прямоугольную периодичность с тем же периодом. Здесь  (,) - двумерный номер базисной функции, а величиныимеют смысл пространственных частот. Иногда пространственными частотами называют целочисленные величиныи.

Коэффициенты Фурье ряда  (3.22) образуют двумерный частотный спектр сигналаи определяются формулой прямого преобразования Фурье:

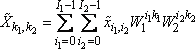(3.24)

Выражение (3.22), восстанавливающее сигнал по его спектру, является обратным преобразованием Фурье. В справедливости преобразований  (3.22) и (3.24), называемых двумерным ДПФ, можно убедиться, подставив (3.24) в (3.22) и приведя правую часть полученного равенства к значению левой, т.е. к.

Заметим, что для точного представления дискретного сигнала с двумерным периодомэлементов согласно формулам БПФ достаточно конечного  числа базисных функций (3.23) - ряд (3.22) является конечным. Это и понятно, поскольку сам представляемый сигнал содержит в одном периоде конечное число точек, т.е. имеет конечное число степеней свободы. Ясно, что число степеней свободы в спектре не может отличаться от числа степеней свободы в самом сигнале.

19. Анализ линейной системы (связь между входным и выходным сигналами, импульсный отклик, представление системы в частотной области).

Импульсный отклик – это отклик системы, когда на нее подали единичный импульс

Характеристика сама по себе возникает на выходе.

Преобразование Фурье входного сигнала x(t) и выходного сигнала y(t) соответственно обозначим как

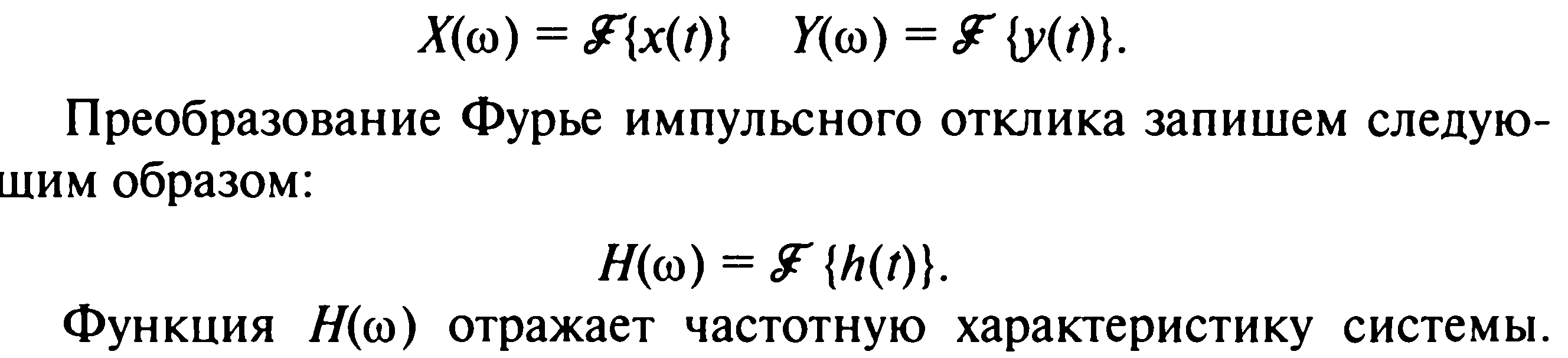
20. Класс несинусоидальных ортогональных функций (функции Радемахера, функции Хаара, функции Уолша).

Функции Радемахера получаются из синусоидальных функций с помощью соотношения

, (3.1)

где аргумент t – безразмерное время, т.е. время, нормированное к произвольному интервалу , а целое положительное числоk – порядок функции. Символом sign (сигнум-функция) обозначается функция:

(3.2)

Функции Радемахера принимают одно из двух значений и имеют вид меандра.

Функции Радемахера ортонормированны с единичной весовой функцией на интервале , т.к. для любых двух функций,имеют место соотношения:

(3.3)

Все функции Радемахера являются нечетным и относительно середины интервала определения и не могут быть использованы для аппроксимации сигналов, четных относительно этой точки. Иными словами, система функций Радемахера – неполная.

Обозначив для краткости r(m,t)=r_m(t), для N=8 будем иметь:

Если =++++----; =++--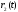++--;=+-+-+-+-, где “+” +1, а “–” –1.

Функции Уолша, образующие полную ортонормированную систему, можно сформировать, образуя произведения соответствующих функций Радемахера.

wal(0,t)=++++++++; wal(1,t)=r₁=++++----; wal(2,t)=r₁r₂=++----++; wal(3,t)=r₂=++--++--

wal(4,t)=r₂r₃=+--++--+; wal(5,t)=r₁r₂r₃=+--+-++-; wal(6,t)=r₁r₃=+-+--+-+;

wal(7,t)=r₃=+-+-+-+-. Сопоставление этих функций с функциями Радемахера позволяет составить очевидные соотношения, согласно которым каждая функция Уолша wal(n,t) с номером n , входящая в систему из функций, является произведением степеней первыхn функций Радемахера.

Используя символ для обозначения операции поразрядного сложения по модулю 2, способ построения функций Уолша можно выразить аналитически для любогов виде следующего соотношения:

Множество функций Хаара har(n,m,t) (рис. 8.1), образующих периодическую, ортонормированную и полную систему функций, было предложено в 1910 году. Рекуррентное соотношение, позволяющее получить har(n,m,t), имеет вид