8. Виды разделяющих функций. Классификатор по минимальному расстоянию

_{А. Линейные разделяющие функции.}

_{В этом} случае в качестве _{Di (x)}используется линейная комбинация измеренных признаков x₁ , x₂ ,…, x_n

B. Классификатор по минимальному расстоянию.

При классификации по минимальному расстоянию относительно R₁, R₂,…, R_m, входной сигнал X предполагается принадлежащим ω_i, т.е.

X~ω_i , если |X − R_i|минимально , где |X − R_i|есть расстояние между X и R_i .

Расстояние можно определить, например, следующим образом

2.2

где индекс T определяет операцию транспонирования вектора.

Так как X^T X не зависит от i, то соответствующая разделяющая функция для классификатора по минимальному расстоянию имеет вид

Классификатор по минимальному расстоянию является линейной функцией. Свойства классификатора по минимальному расстоянию конечно зависят от того, как выбраны опорные векторы.

С. Кусочно-линейная разделяющая ф-я. разделяющая функция в данном случае имеет вид

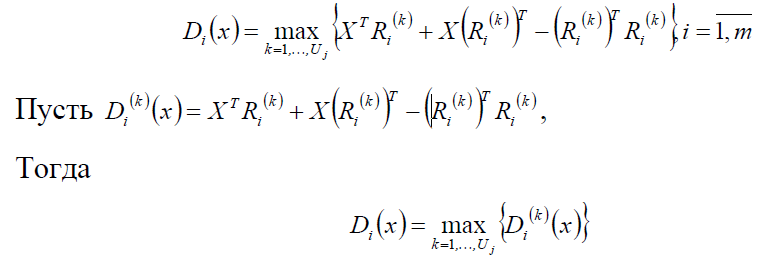
Следует отметить, что D_i^(k)(x) является линейной комбинацией признаков. Поэтому указанный классификатор часто называют кусочно-линейным классификатором.

D. Полиномиальная разделяющая функция.

Полиномиальная функция r -ой степени может быть представлена в виде

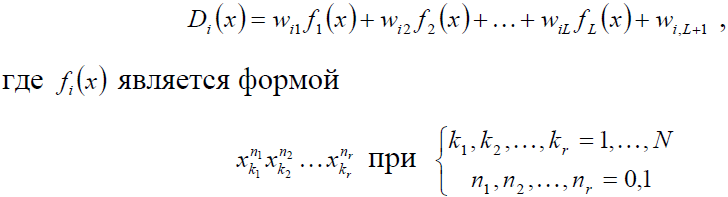
Решающая граница между двумя классами также имеет форму полинома r-ой степени. В частности, если r = 2 , решающая функция называется квадратичной.

В этом случае

Разделяющая функция будет иметь вид

где L =1/ 2N(N + 3)

9. Задача двухклассового распознавания

Систему распознавания образов с применением ортогональных преобразований можно представить в виде

Через x(t) обозначается сигнал , принадлежащий одному из K классов C₁ ,C₂ …, ,C_K . На первом этапе выбора осуществляется ортогональное преобразование. Вторым этапом выбора признака является понижение размерности, после чего получаем подмножество M признаков z₁ , z₂ ,… , z_М из {Y(M)}= {Y(1),Y(2),K,Y(N)} причём M << N .

Понижать размерность следует таким образом , чтобы сопутствующее этому увеличение ошибки классификации было относительно невелико. Классификатор, изображенный на рис. 23.1 является решающим устройством, которое обучается с целью классификации входного сигнала x(t), принадлежащего к одному из K классов.

10. Классификатор для распознавания 3-х и k классов образов по критерию наименьшего среднеквадратического расстояния

11. Метод отображения по алгоритму наименьших квадратов

При обсуждении классификаторов, работающих по критерию наименьшего расстояния, предполагалось, что классы образов в пространстве признаков группируются вокруг соответствующих им средних Zi (i =1,2,K,K) . Однако, возможен и другой подход. При этом классификатор должен в первую очередь отображать образы в пространство решений, в котором образы , принадлежащие i C обязательно группируются вокруг заранее выбранной точки i V . Преобразование A , которое позволяет осуществлять это отображение из пространства признаков в пространство решений в общем случае выбирается таким , чтобы общая среднеквадратичная ошибка была минимальной .Для классификации некоторого образа этот образ сначала отображается в пространство решений, а затем классифицируется как принадлежащий io C , если он отображён ближе к точке io V . Введём отображение по методу наименьших квадратов, на котором основываются классификаторы с минимальным среднеквадратичным расстоянием .

Рассмотрим множество M - мерных образов ij Z , i j =1,2,K, N , которые должны отображаться в определённую точку в K - мерном пространстве , обозначаемую _______[ ] i k V v ,v , ,v = 1 2 K . Найдём преобразование A , которое отображает { } ij Z в точку i V , таким образом, чтобы общая среднеквадратичная ошибка, вызываемая отображением , была минимальной. Обозначим результат отображения образа ij Z через ij L . Тогда

соответствующий вектор ошибки будет равен

21.5

Из выражения (25.1) следует , что общая среднеквадратичная ошибка при

отображении ij Z в i V определяется как