2 Составляющие процесса эксплуатационного обслуживания технических средств информационных систем Выбор контролируемых параметров. Построение схемы поиска неисправностей

Пример 2.1. Построить граф связей параметров по статистическим данным о вероятностных связях характеристик технического устройства, представленным в табл. 2.1.

Таблица 2.1

Нормированная корреляционная матрица связей параметров

технического объекта

	х1	х2	х3	х4	х5	х6	х7	х8	х9	х10
х1	1	0,91	0,23	-0,35	0,42	-0,17	-0,16	0,05	0,53	-0,07
х2	0,91	1	0,38	-0,32	0,02	0,48	-0,61	0,75	0,97	-0,01
х3	0,23	0,38	1	0,43	-0,09	0,69	-0,27	0,76	-0,06	0,98
х4	-0,35	-0,32	0,43	1	0,31	-0,19	0,24	0,63	-0,29	0,59
х5	0,42	0,02	-0,09	0,31	1	0,52	-0,05	-0,19	0,06	0,11
х6	-0,17	0,48	0,69	-0,19	0,52	1	-0,12	0,70	0,56	-0,63
х7	-0,16	-0,61	-0,27	0,24	-0,05	-0,12	1	0,39	-0,20	0,67
х8	0,05	0,75	0,76	0,63	-0,19	0,70	0,39	1	0,54	0,03
х9	0,53	0,97	-0,06	-0,29	0,06	0,56	-0,20	0,54	1	-0,02
х10	-0,07	-0,01	0,98	0,59	0,11	-0,63	0,67	0,03	-0,02	1

Р е ш е н и е. Граф связей параметров строится по следующему алгоритму [2]:

• Находим в матрице связей максимальный по абсолютной величине (недиагональный) элемент k_ij.

• Параметры с номерами i и j обозначаем кружками и соединяем линией, над которой записываем значение коэффициента связи (коэффициента корреляции) между ними.

• В строках i и j находим следующий после k_ij максимальный по абсолютной величине элемент, например .

• Параметр – с номером обозначаем на графике кружком и соединяем с элементом j.

• В матрице связей вычеркиваем столбцы, соответствующие номерам .

• Среди оставшихся элементов строк j и находим максимальный по абсолютной величине элемент.

Эти действия проводим до тех пор, пока на графике не будет столько вершин, сколько рассмотрено параметров.

Построенный по данному алгоритму граф связей параметров, соответствующий исходным данным табл. 2.1, изображен на рис.2.1.

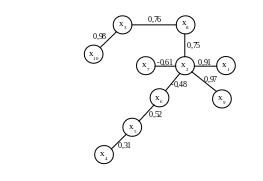
Рис.2.1. Граф связей параметров, соответствующий табл.2.1

Пример 2.2. В условиях примера 2.1 выделить параметры подлежащие контролю при выполнении технического обслуживания объекта. Считаем, что пороговое значение коэффициента связи параметров k₀ = 0,8. Известно, что параметр х₃ измерить затруднительно. Измерение параметра х₂ связано с нарушением безопасности человека, проводящего измерение; параметр х₁ не является значимым.

Р е ш е н и е. По графу связей параметров рис.2.1 выделяем группы параметров так, чтобы значения коэффициентов связи между ними были бы больше k₀. Получаем следующие группы сильно связанных параметров:

{х₁, х₂, х₉}, {х₃, х₁₀}, {х₄}, {х₅}, {х₆}, {х₇},{х₈}.

Учитывая условия измерения и значимость параметров, выбираем из всей совокупности параметров следующие:

х₄, х₅, х₆, х₇, х₈, х₉, х₁₀.

Пример 2.3. Устройство состоит из восьми элементов: А, Б, В, Г, Д, Е, Ж, З. Составить технологическую схему последовательного поиска неисправного элемента.

Р е ш е н и е. Начальное состояние системы обозначим 11111111. При первой проверке П_00111111 определяется состояние элементов А и Б. Положительному результату проверки (элементы А и Б работоспособны) соответствует состояние 00111111. Отрицательному результату проверки, когда один из элементов А или Б неисправен, причем, неизвестно, какой именно, соответствует состояние 11000000. Элементы В, Г, Д, Е, Ж, З считаются исправными в соответствии с допущением об отказе лишь одного элемента.

После состояния 11000000 с помощью проверки П_01111111 или П_10111111 определяется, какой элемент неисправен: А или Б. После состояния 00111111 проводится проверка, разделяющая непроверенные элементы на две подгруппы, например: П_11001111 или П_11010111 и др. Чем больше элементов в системе, тем больше различных путей поиска неисправного блока.

Возможный вариант технологической схемы последовательного поиска неисправного элемента для условия примера представлен на рис. 2.2.

Рис.2.2 Технологическая схема последовательного поиска неисправного элемента в системе из восьми элементов

Пример 2.4. Оценить достаточность проверок П11101011; П11000111; П00110111 для определения исправности элемента Е в системе, состоящей из элементов А, В, Г, Д, Е, Ж, З.

Р е ш е н и е. Для оценки достаточности совокупности проверок в отношении элемента Е перепишем каждое, основное или дополнительное, обозначение трёх проверок так, чтобы в разряде, соответствующем рассматриваемому элементу, всегда были нули. Затем эти обозначения пишутся одно под другим и складываются единицы в соответствующих разрядах:

П 11101011

00111000

11001000

^{------------------------}

22213011

Совокупность проверок достаточна, так как во всех разрядах, кроме соответствующего элементу Е, отсутствуют нули. Достаточно и двух первых проверок.

Пример 2.5. Устройство состоит из восьми элементов, для которых известны значения условных вероятностей того, что i-й элемент неработоспособен при условии, что отказ устройства произошел (см.табл.2.2). Считая, что значения среднего времени выполнения проверок одинаковы, составить оптимальную технологическую схему поиска неисправностей, минимизирующую число проверок.

Таблица 2.2

Значения условных вероятностей отказа элементов

при условии отказа системы

Обозначения элементов хi	х1	х2	х3	х4	х5	х6	х7	х8
Значения условных вероятностей	0,25	0,15	0,12	0,02	0,18	0,22	0,05	0,01

Р е ш е н и е. Выписываем обозначения элементов столбиком в порядке уменьшения условных вероятностей . Затем последние два элемента с наименьшими значениями группируются вместе и вероятности для них складываются. В полученный после этой операции вспомогательной совокупности элементы опять располагаются в порядке уменьшения значений и вновь складываются наименьшие значения вероятностей. Эта операция выполняется до тех пор, пока не останется один элемент с вероятностью . Эта процедура для условий примера приведена на рис. 2.3.

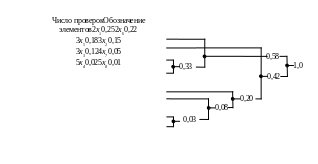
Рис.2.3. Получение оптимальной структуры схемы поиска неисправностей

Из схемы рис.2.3 находим необходимое число проверок, равное числу объединений на пути от рассматриваемого элемента до последнего объединения элементов, имеющего вероятность . Оптимальную схему состояний получаем формальным перестроением полученной схемы: точкам объединений элементов соответствуют проверки (разветвления) на схеме состояний. Структура оптимальной схемы поиска неисправностей представлена на рис.2.4.

Рис.2.4. Оптимальная структура схемы поиска неисправностей

Выбор экономически оптимальной структуры системы восстановления. Определение количества специалистов при централизованной системе восстановления

Пример 2.6. Комплекс технических средств АСУ “Экспресс” размещается N=9 территориально разобщённых кассовых залах (КЗ). Примем условно, что во всех кассовых залах функционирует N=169 АРМ. Все АРМ одного и того же класса со следующими характеристиками: значение параметра потока отказов одного АРМ 1/ч; значение среднего времени восстановления работоспособности АРМ m_tв = 0,8 ч.

Возможны две различные структуры системы технического обслуживания (СТО) АРМ:

• децентрализованная структура (ДТО), при которой каждый КЗ имеет склад запасных элементов, обслуживающий персонал, ремонтное оборудование; при каждом КЗ имеется штат ремонтников, который (с учётом резерва) составляет 3,5 бригады; КТС работают круглосуточно при трёхсменной работе специалистов;

• централизованная структура (ЦТО), при которой все трудовые и материальные ресурсы централизованы в органе технического обслуживания (ОТО).

Предположим, что время доставки бригады ремонтников от места возможного размещения ОТО до каждого из КЗ одинаково и равно t_д = = 0,3ч. Стоимость одного транспортного средства С_тр = 140000 руб. при сроке окупаемости 5 лет. Стоимость С_п одного часа простоя АРМ составляет 120 руб. Число ремонтных бригад S в ОТО может варьироваться.

Определить экономически оптимальную структуру СТО, при которой значение коэффициента готовности каждого АРМ не менее 0,9890.

Р е ш е н и е. В качестве экономического критерия качества функционирования СТО будем использовать суммарные затраты и потери в единицу времени работы АРМ:

,

где W_пр – средние потери в единицу времени простоя АРМ; З_то – средние затраты на техническое обслуживание в единицу времени работы АРМ.

Для оценки надёжности функционирования СТО используется коэффициент готовности АРМ k_гi (i=1N). Так как время доставки бригады от ОТО до различных КЗ при ЦТО принято одинаковым, можно считать, что k_гi =k_г при i = 1,..., N. При этом потери W_пр при любой структуре СТО можно определить следующим образом:

W_пр = С_п(1-k_г)∙N.

При одинаковом количестве бригад в каждую смену средние расходы на содержание бригад в единицу времени работы АРМ

,

где T_мес – месячная наработка АРМ. Амортизационные отчисления З_тр от приобретения одного транспортного средства в единицу времени работы АРМ

,

где Т_А – предполагаемая наработка АРМ в срок амортизации транспортного средства.

При ДТО транспортные расходы отсутствуют. Следовательно, критерий L_ при ДТО можно представить в виде:

.

Можно считать, что при ДТО средняя продолжительность простоя АРМ при появлении отказа , а коэффициент готовности АРМ

.

Таким образом, для децентрализованной системы технического обслуживания получаем:

;

; (2.1)

. (2.2)

Будем считать, что при ЦТО число транспортных средств равно числу бригад. Тогда критерий L_ при ЦТО с S обслуживающими бригадами

.

Для определения коэффициента готовности АРМ при централизованной структуре СТО можно составить математическую модель её работы, используя теорию массового обслуживания. В качестве обслуживающих каналов будем рассматривать бригады ремонтников. Заявки на обслуживание отказавших АРМ образуют поток требований к системе. Примем следующие допущения:

• поток требований к системе является пуассоновским;

• распределение времени обслуживания одной заявки подчиняется экспоненциальному закону.

При ЦТО среднее время обслуживания одной заявки включает среднее время доставки бригады из ОТО в КЗ:

= m_tв + t_д = 0,8 + 0,3 = 1,1 ч.

Так как число ремонтных бригад S < N, возможно возникновение очереди заявок на обслуживание отказавших АРМ. Поэтому средняя продолжительность простоя АРМ при появлении отказа в случае ЦТО с S обслуживающими бригадами

,

где t_ож – среднее время ожидания одной заявки в очереди на обслуживание.

Схема состояний системы массового обслуживания, состоящей из N АРМ и S ремонтных бригад, представлена на рис. 2.5, где

.

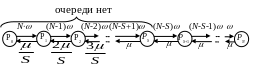
Рис.2.5 Схема состояний системы массового обслуживания

При решении соответствующей системы уравнений в установившемся режиме используем следующие известные формулы расчёта вероятностей состояний системы:

;

, ;

, ,

где .

Среднее число АРМ , находящихся в неработоспособном состоянии

.

Для различных значений S получены следующие значения (см. табл. 2.3, столбец 2)

Величина равна

.

Значения для различных S см. в табл. 2.3 , столбец 3.

Тогда коэффициент готовности АРМ при ЦТО с S обслуживающими бригадами

Значения и для различных значений S см. в табл. 2.3, столбцы 4, 5.

Таблица 2.3

Результаты расчёта экономически оптимальной структуры ЦТО

S
1	2	3	4	5
1	78,09	85,90	0,5379	9423,24
2	6,95	4,289	0,9589	937,21
3	2,378	1,427	0,9859	441,51
4	1,947	1,165	0,9884	442,65
5	1,862	1,114	0,9889	484,37
6	1,843	1,102	0,9890	534,25
7	1,839	1,101	0,9891	584,01
8	1,838	1,100	0,9891	635,86

Как видно из (2.1), (2.2) и данных табл.2.3, наложенные на k_г ограничения выполняются для ДТО и ЦТО при S  6. По результатам анализа выбираем вариант ЦТО с S = 6, т.к. при нём удовлетворяется требование к k_г и имеет место минимальное по сравнению с вариантами ДТО и ЦТО S  7 значение L_ .