Спутник летит от перигея до апогея.

Естественно, что при построении положения спутника на орбите, угол Θ – истинную аномалия - нужно откладывать тоже от направления на перигей – противоположную старту точку орбиты.

Пробная задача № 2.

Задана стартовая скорость V_{ст. =} 6,5 км/с., направленная параллельно к поверхности Земли и H_ст = 2000 км. – стартовая высота. Определите все, какие сможете, характеристики его движения, и положение спутника на орбите через 45 минут после старта. Так же в этот момент необходимо определить его высоту над поверхностью Земли и скорость.

Если Вы всё сосчитали правильно, то должно получиться:

Θ = 322^о,8

r = 6792 км.

H = 414 км.

V = 8,02 км/сек.

Рисунок к задаче должен быть примерно таким:

Рис. 3

Значительно более интересная ситуация в том случае, если величина стартовой скорости была недостаточной для вывода спутника на орбиту и он упал на Землю. Это третий вариант задачи первого типа.

Рис. 4

На рисунке 4 показана орбита такого спутника в предположении, что он свободно двигается сквозь вещество Земли и вся масса Земли состредоточена в её центре. Это конечно совершенно абстрактная ситуация, но она помогает лучше понять законы движений ИСЗ. Точно так же , как и в двух предыдущих задачах, определяете все характеристики движения ИСЗ : а – большую полуось такой мысленной орбиты, Т – период обращения, q и Q – перигейное и апогейное расстояния, e - эксцентриситет, H_{Q -} высоту в апогее и H_{q –} высоту в перигее. Последняя высота, как легко сообразить, будет отрицательной.

Самое трудное в этой задаче – это определить, как далеко упадет спутник, и сколько времени он будет находиться в полете. Это делается следующим образом.

Прежде всего находим истинную аномалию точки К₁ – точки падения. Для этого воспользуемся уравнением (4) – уравнением эллипса в полярных координатах:

Радиус вектор точки падения равен радиусу Земли, величины и е найдены ранее. Разрешая это уравнение относительно Θ, получим два значения истиной аномалии. Одно выдаст калькулятор, второе, учитывая знаки косинуса по четвертям, присваиваем сами. Одно значение соответствует точке падения ИСЗ - К₁ , второе – точке К₂ – точке «вылета из под Земли». Радиус вектор этой точки тоже равен радиусу Земли. Из рисунка совершенно очевидно, что истинная аномалия точки падения обязательно больше 180 градусов. Такое значение и выбираем. Обозначим его Θ₁ .

Из рисунка так же понятно, что Θ_ст - истинная аномалия точки старта –

обязательно равна 180 градусам.

Значит, дуга КК₁ = L^о = Θ₁ - Θ_ст . Это и есть дальность полета ИСЗ. Мы определили её величину в градусах.

Чтобы выразить её в километрах – L_км - достаточно вспомнить, что 2π R_  - длина дуги большого круга на поверхности Земли соответствует 360 градусам. Значит, зная радиус Земли, можно сосчитать количество километров, приходящихся на один градус или на КК₁ градусов.

Несколько сложнее определить время полета ИСЗ до падения. Это делается следующим образом.

Зная истинную аномалию точки падения - Θ₁ - и используя уже известное соотношение:

tg(Θ₁/2) = [(1+e)/(1-e)]^0,5 ×tg (E/2)

находим эксцентрическую аномалию – Е.

Через эксцентрическую аномалию точки падения находим её среднюю аномалию, используя соотношение:

E = M +57^о,296 × e× sin E

Знание средней аномалии – M - позволяет определить ∆t₁ - время полета спутника от точки перигея до точки падения. Для этого воспользуемся выражением:

М = 360^о/T×∆t₁

Ещё раз обращаю внимание на то, что найденное значение ∆t₁ - это время «полета» спутника от точки П – перигея до точки К₁ - точки падения.

Поскольку от перигея до апогея спутник «летит» полпериода, значит для определения времени полёта его от точки старта (а это апогей) до точки падения - ∆Т - нужно из найденного ∆t₁ вычесть полпериода обращения спутника вокруг Земли:

∆Т = ∆t₁ - T/2

Пробная задача № 2.

Задана стартовая скорость V_{ст. =} 6,3 км/с., направленная параллельно к поверхности Земли, и H_ст = 2000 км. – стартовая высота. Определите все, какие сможете, характеристики его движения, дальность и время полёта ИСЗ до падения.

Если Вы всё рассчитали правильно, то у Вас получится, что:

L = 13658 км.

∆Т = 2314 сек.

Осталось сделать рисунок, примерно отражающий картину полёта. Он должен выглядеть примерно следующим образом:

А

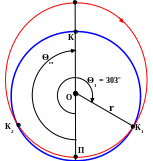
Рис. 5