67. Предприятие обеспечивает регулярный выпуск продукции при безотказной поставке комплектующих от двух смежников. Вероятность отказа в поставке продукции от пер­вого из смежников равна 0,05, от второго — 0,08. Найти веро­ятность сбоя в работе предприятия.

68. Предположим, что вероятность выловить рыбу при одной поклевке равна 0,7. Какова вероятность того, что рыбак поймает хотя бы одну рыбу, если у него четыре поклевки?

69. Студент в сессию должен сдать 3 экзамена, причем известно, что положительную оценку он может получить за них с вероятностями 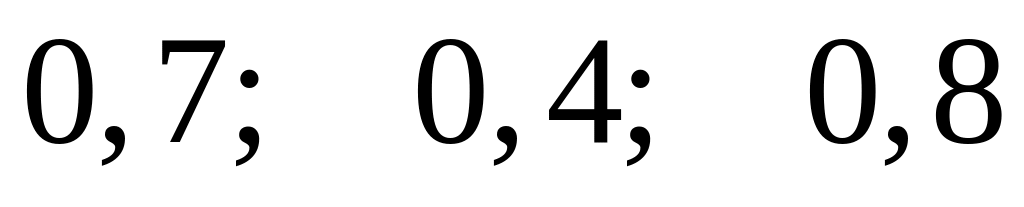. Предполагая, что различные экзамены представляют собой независимые испытания найти вероятности того, что студент: а) не сдаст ни одного экзамена; б) студент сдаст ровно два экзамена; в) студент сдаст хотя бы один экзамен.

70. В магазине имеются 10 женских и 6 мужских шуб. Для анализа качества отобрали три шубы случайным образом. Определить вероятность того, что среди отобранных шуб ока­жутся:

а) только женские шубы;

б) только мужские или только женские шубы.

71. На предприятие поступают заявки от нескольких тор­говых пунктов. Вероятности поступления заявок от пунктов А и В равны соответственно 0,5 и 0,4. Найти вероятность пос­тупления заявок от пункта А или от пункта В, считая события поступления заявок от этих пунктов независимыми, но сов­местными.

72. Вероятности своевременного выполнения задания тремя независимо работающими предприятиями соответ­ственно равны 0,5; 0,6; 0,7. Найти вероятность своевременного выполнения задания хотя бы одним предприятием.

73. Три стрелка производят по одному выстрелу в мишень. Вероятность попадания в цель для первого стрелка равна 0,6; 0,7 для второго и 0,5 для третьего. Найти вероятность того, что цель будет поражена.

74. Вероятности своевременного выполнения задания тремя независимо работающими предприятиями соответ­ственно равны 0,5; 0,6; 0,7. Найти вероятность своевременного выполнения задания хотя бы одним предприятием.

75. Покупатель может приобрести акции трех компаний: А, В и С. В течение следующего года надежность первой компании оценивается экспертами в 99%, второй – в 98%, третьей - 97%. Чему равна вероятность того, что наступит банкротство хотя бы одной компании?

76. Вероятность получить высокие дивиденды по акциям на первом предприятии - 0.1, на втором - 0.2, на третьем – 0.25. Определить вероятность того, что акционер, имеющий акции всех предприятий, получит высокие дивиденды: а) на всех предприятиях; б) только на одном предприятии; в) хотя бы на одном предприятии.

77. В магазине выставлены для продажи 20 изделий, среди которых 4 изделий некачественных. Какова вероятность того, что взятые случайным образом 3 изделия будут:

а) качественными;

б) хотя бы один из них будет качественным;

в) ни одного качественного изделия.

Формулы Бернулли и Пуассона

Если при проведении испытаний вероятность появления события А не зависит от исходов других испытаний, то такие испытания называ­ются независимыми.

Формула Бернулли определяет вероятность появления ровно т раз события А в серии из п независимых испытаний, в каждом из которых вероятность появления события А равна р:

В ряде случаев требуется определить вероятности появления события А менее т раз (X < т), более т раз (X > т), не менее т раз (X > т), не более т раз (X < т). В этих случаях могут быть использованы фор­мулы

При больших п и малых р вычисления по формуле Бернулли затруд­нены. В этих случаях обычно используется формула Пуассона

78. В результате обследования были выделены семьи, имеющие по четыре ребенка. Считая вероятности появления мальчика и девочки в семье равными, определить вероятности появления в ней:

а) одного мальчика;

б) двух мальчиков.

В) четырех мальчиков

Г) четырех девочек

79. Работают четыре магазина по продаже стиральных ма­шин. Вероятность отказа покупателю в магазинах равна 0,1. Считая, что ассортимент товара в каждом магазине формиру­ется независимо от других, определить вероятность того, что покупатель получит отказ

А) в двух магазинах.

Б) в трех магазинах

В) в четырех магазинах

80. Студент приобрел пять лотерейных билетов. Вероятность выигрыша по одному билету составляет 0,2. Найти вероятность того, что студент выиграет:

а) по трем лотерейным билетам;

б) не менее чем по трем билетам;

в) хотя бы по одному билету.

г) Определить наивероятнейшее число выигрышных билетов.

81. Четыре покупателя приехали на оптовый склад. Ве­роятность того, что каждому из этих покупателей потребуется холодильник марки «А», равна 0,4. Найти вероятность того, что холодильник потребуется:

а) не менее чем двум покупателям;

б) не более чем трем покупателям;

в) всем четырем покупателям.

82. Каждый из пяти лифтов в высотном доме в течение месяца работает нормально с вероятностью 0,9. Найти вероятность того, что в течение месяца будут работать нормально:

а) 3 лифта; б) более 3 лифтов.

83. В среднем по 15 % договоров страховая компания выплачивает страховую сумму. Найти вероятность того, что из 10 договоров с наступлением страхового случая будет связано с выплатой страховой суммы:

а) три договора;

б) менее двух договоров.

В) ни одного договора

Г) все 10 договоров

84. Фирма снабжает своей продукцией пять магазинов. От каждого магазина может поступить заявка на очередной день с вероятностью 0.4 независимо от заявок других магазинов.

1. Какова вероятность того, что поступит ровно две заявки?

2. Какова вероятность того, что поступит не более двух заявок?

3. Какова вероятность, что количество поступивших заявок будет лежать в пределах от двух до четырех?

4. Какова вероятность, что не поступит ни одной заявки?

5. Найти наивероятнейшее число заявок в день и вероятность получения именно такого числа заявок?

85. Банк имеет семь отделений. Ежедневно с вероятностью 0,3 каждое отделение, независимо от других, может заказать на следующий день крупную сумму денег. В конце рабочего дня один из вице-президентов банка знакомится с посту- пившими заявками. Найти вероятности следующих событий:

1. поступили ровно три заявки;

2. поступила хотя бы одна заявка;

3. среди поступивших двух заявок есть заявка от первого отделения;

4. поступило не более двух заявок;

5. поступило от 2 до 5 заявок.

86. В новом микрорайоне поставлено 10000 кодовых замков на входных дверях домов. Вероятность выхода из строя од­ного замка в течение месяца равна а) 0,0002; б) 0,001. Найти вероятность того, что за месяц откажут два, три и пять замков.

87. Завод отправил в торговую сеть 500 изделий. Вероят­ность повреждения изделия в пути равна 0,002. Найти веро­ятность того, что при транспортировке будет повреждено:

а) ровно три изделия;

б) более трех изделий.

88. На станциях отправления поездов находится 1000 ав­томатов для продажи билетов. Вероятность выхода из строя одного автомата в течение часа равна 0,004. Какова вероят­ность того, что в течение часа из строя выйдут два, три и пять автоматов?

89. Вероятность выпуска бракованной микросхемы равна 0,002. Какова вероятность того, что из 2000 присланных в магазин микросхем окажется не менее 3 бракованных?

90. Всхожесть семян огурцов равна 0,8. Какова вероятность того, что из пяти посеянных семян взойдут не менее четырех?

91. Обувной магазин продал 200 пар обуви. Вероятность того, что в магазин будет возвращена бракованная пара равна 0,01. Найти вероятность того, что из проданных пар обуви будет возвращено а) ровно 4 пары, б) ровно 5 пар.

92. Завод производит мобильные телефоны. Вероятность того, что выпущенный телефон бракованный, равна 0,015. Найти вероятность того, что в партии из 200 телефонов окажется хотя бы один бракованный.

93. Вероятность повреждения бутылки с минеральной водой при перевозке равна 0,002. Найти вероятность того, что из 2000 бутылок при перевозке будет повреждено менее двух.

94. Владельцы кредитных карт ценят их и теряют весьма редко — вероятность потерять кредитную карту в течение недели для случайно выбранного вкладчика составляет 0,001. Банк выдал кредитные карты 2 000 клиентам. Найти:

1. вероятность того, что за предстоящую неделю будет утеряна ровно одна кредитная карта;

2. вероятность того, что за предстоящую неделю будет утеряна хотя бы одна кредитная карта;

3. вероятность того, что за предстоящую неделю будет утеряно не более трех кредитных карт;

4. наиболее вероятное число кредитных карт, теряемых за месяц.

95. Прядильщица обслуживает 1000 веретен. Вероятность обрыва нити на одном веретене в течение одной минуты равна 0,004. Найти вероятность того, что в течение одной минуты обрыв произойдет:

а) на пяти веретенах;

б) хотя бы на двух веретенах