МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ

Волгоградский государственный университет

Ю.В. Зайцева Лабораторные по курсу эконометрики для магистров

Волгоград 2017

Лабораторная работа № 1. Модели множественной регрессии

Задание 1. (Построение модели линейной множественной регрессии в пакете Excel). Имеются данные о потреблении мяса в США B в 1980 – 2007 годах (фунты на душу населения), и его зависимости от цены P (центы за фунт) и личного располагаемого дохода YD (тысячи долларов в расчете на душу населения).

1. Скопировать из файла данные для своего варианта. Должно получиться 3 столбца YD, B, P.

2. Постройте линейную модель множественной регрессии, объясняющую динамику потребления мяса в США в зависимости от цены и личного располагаемого дохода. Для этого выберите в меню Данные – Анализ данных – Регрессия. Если этой команды нет в меню, необходимо загрузить надстройку Пакет анализа через команду Сервис.

3. Дайте подробную интерпретацию коэффициентам полученной модели.

4. Чему равен коэффициент детерминации модели? Что он показывает?

5. Проверьте значимость отдельных коэффициентов модели и всей модели в целом (уровень значимости 0.1).

6. Постройте модели парной линейной регрессии, в которых потребление мяса в США объясняется изменением только одного фактора. Сравните их с моделью множественной регрессии: в чем заключается преимущество модели множественной регрессии?

7. Рассчитайте средние эластичности объема потребления мяса по цене и по доходу. Для расчета применяется формула 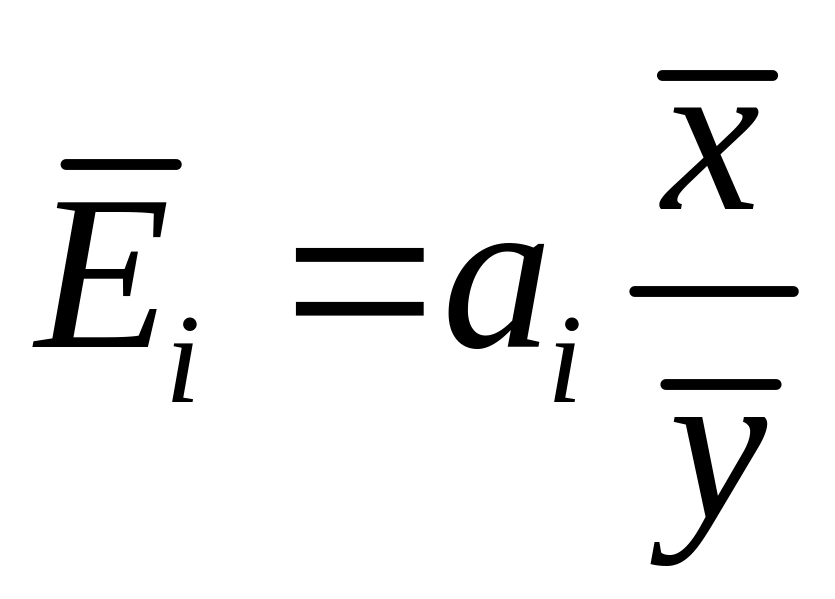. Дайте интерпретацию полученным эластичностям. Сравните силу влияния каждого из факторов на потребление мяса.

8. Постройте прогноз потребления мяса для цены 30 центов за фунт и личного располагаемого дохода 7 тыс. долл.

Задание 2. (Построение модели степенной множественной регрессии в пакете Excel).

1. Создайте столбцы, содержащие логарифмы исходных данных.

2. Постройте степенную модель множественной регрессии, объясняющую динамику потребления мяса в США вида

.

Если прологарифмировать эту модель, мы получим (если непонятно как такое получилось, вспоминаем школьную математику – свойства логарифмов). Модель в логарифмах является линейной, а значит ее можно построить в Excel, задав в качестве зависимой переменной ln(B), а в качестве независимых ln(P) и ln(YD).

Запишите полученное уравнение. Не забудьте от модели в логарифмах перейти к исходной модели.

3. Дайте интерпретацию коэффициентам степенной модели.

4. Проверьте значимость отдельных коэффициентов модели и всей модели в целом (уровень значимости 0.1).

5. Рассчитайте эластичности объема потребления мяса по цене и по доходу. Дайте интерпретацию полученным эластичностям. Сравните силу влияния каждого из факторов на потребление мяса.

6. Постройте прогноз потребления мяса для цены 30 центов за фунт и личного располагаемого дохода 7 тыс. долл. по степенной модели.

7. Какую из двух моделей вы бы выбрали?

Лабораторная работа № 2. Бинарные переменные в моделях множественной регрессии

Имеются данные по однокомнатным квартирам, выставлявшимся на продажу в Москве:

Region	район;
Distc	удаленность от центра, км.;
Distm	удаленность от метро, мин.;
Totsq	общий метраж, кв.м.;
Kitsq	площадь кухни, кв.м.;
Livsq	площадь комнаты, кв.м.;
Floor	этаж (0,1) 0 – первый или последний, 1 – средний;
Cat	категория дома (0,1), 1 – кирпичный, 0 – панельный;
Price	цена, тыс. USD.

Задание 1. (Линейная модель множественной регрессии)

1. Скопировать из файла данные для своего варианта. Значения объясняющих переменных для всех вариантов одинаковы. Значения объясняемой переменной Price – по вариантам.

1. Постройте уравнение регрессии, характеризующее зависимость цены от всех факторов в линейной форме.

2. Оцените значимость полученного уравнения (уровень значимости 0,05).

3. Определите, какие факторы значимо воздействуют на формирование цены квартиры в этой модели (уровень значимости 0,05).

4. Вам необходимо проверить предположение о том, что квартиры на средних этажах при прочих равных факторах стоят дороже, чем квартиры на средних этажах. Сформулируйте основную и альтернативную гипотезы. Проверьте гипотезу (уровень значимости 0,05). Сделайте вывод.

5. Вам необходимо проверить предположение о том, что квартиры в кирпичных домах при прочих равных факторах стоят дороже, чем квартиры в панельных домах. Сформулируйте основную и альтернативную гипотезы. Проверьте гипотезу (уровень значимости 0,05). Сделайте вывод.

6. Постройте линейную модель формирования цены квартиры за счет значимых факторов.

7. Дайте интерпретацию коэффициентов построенной модели со значимыми факторами.

Задание 2. (Степенная модель множественной регрессии)

1. Прологарифмируйте все переменные, кроме бинарных.

2. Постройте уравнение регрессии, характеризующее зависимость цены от всех факторов в степенной форме. Окончательное уравнение регрессии должно иметь вид:

Это уравнеие легко можно сделать линейным, прологарифмировав. Если затрудняетесь это сделать, посмотрите построение степенной модели в первой лабораторной работе.

3. Оцените значимость полученного уравнения (уровень значимости 0,05).

4. Определите, какие факторы значимо воздействуют на формирование цены квартиры в этой модели (уровень значимости 0,05).

5. Вам необходимо проверить предположение о том, что квартиры на средних этажах при прочих равных факторах стоят дороже, чем квартиры на средних этажах. Сформулируйте основную и альтернативную гипотезы. Проверьте гипотезу (уровень значимости 0,05). Сделайте вывод.

6. Вам необходимо проверить предположение о том, что квартиры в кирпичных домах при прочих равных факторах стоят дороже, чем квартиры в панельных домах. Сформулируйте основную и альтернативную гипотезы. Проверьте гипотезу (уровень значимости 0,05). Сделайте вывод.

7. Постройте степенную модель формирования цены квартиры за счет значимых факторов.

8. Дайте интерпретацию коэффициентов построенной модели со значимыми факторами.

Задание 3.

1. Выберите лучшую модель. Обоснуйте свой выбор.

2. Используя выбранную модель, осуществите прогноз цены однокомнатной квартиры, находящейся на расстоянии 10 км от центра, 5 мин. ходьбы до метро, общей площадью 35 кв.м, площадью кухни 8 кв.м, жилой площадью 33 кв.м, расположенной на 1-м этаже кирпичного дома.