Та же контрольная по ТПР в PDF

Структурно нейрон можно изобразить следующим образом: входные сигналы — компоненты вектора X - движутся по дендритам и поступают на синапсы, которые изображены в виде (трех) кружочков, там над сигналами осуществляется преобразование L , после чего функция F дает выходной сигнал Y .

n

Текущее состояние нейрона определяется, как взвешенная сумма его входов: s= ∑ xi wi .

i=1

Машинное обучение (Machine Learning) — обширный подраздел искусственного интеллекта, изучающий методы построения алгоритмов, способных обучаться. Различают два типа обучения. Обучение по прецедентам, или индуктивное обучение, основано на выявлении закономерностей в эмпирических данных. Дедуктивное обучение предполагает формализацию знаний экспертов и их перенос в компьютер в виде базы знаний. Дедуктивное обучение принято относить к области экспертных систем, поэтому термины машинное обучение и обучение по прецедентам можно считать синонимами.

Общая постановка задачи обучения по прецендентам. Имеется множество объектов (ситуаций) и множество возможных ответов (откликов, реакций). Существует некоторая зависимость между ответами и объектами, но она неизвестна. Известна только конечная совокупность прецедентов — пар «объект, ответ», называемая обучающей выборкой. На основе этих данных требуется восстановить зависимость, то есть построить алгоритм, способный для любого объекта выдать достаточно точный ответ. Для измерения точности ответов определённым образом вводится функционал качества.

Классификация основных алгоритмов обучения нейронных сетей:

1) Обучение с учителем (supervised learning) - наиболее распространённый случай. Если при обучении классификатора используется эталонное (ожидаемое) значение выходного сигнала нейрона, то такой механизм обучения называется обучением с учителем — результат обучения предопределен заранее благодаря заданным обучающим эталонным значениям. Каждый прецедент представляет собой пару "объект, ответ". Требуется найти функциональную зависимость ответов от описаний объектов и построить алгоритм, принимающий на входе описание объекта и выдающий на выходе ответ. Функционал качества обычно определяется как средняя ошибка ответов, выданных алгоритмом, по всем объектам выборки:

а) Метод коррекции ошибки; б) Правило Розенблатта (дельта-правило):

Метод обучения перцептрона по принципу градиентного спуска по поверхности ошибки. Дельта-правило развилось из первого и второго правил Хебба. Его дальнейшее развитие привело к созданию метода обратного распространения ошибки. :

Формула: w i t+1 =w i t +α xi D−Y ,i= 1, . .. , n , где

(Подробный алгоритм обучения по правилу Розенблатта описан в решении Задания 2.2); в) Метод обратного распространения ошибки:

Это итеративный градиентный алгоритм, который используется с целью минимизации ошибки работы многослойного перцептрона и получения желаемого выхода. Основная идея этого метода состоит в распространении сигналов ошибки от выходов сети к её входам, в направлении, обратном прямому распространению сигналов в обычном режиме работы. Алгоритм обратного распространения ошибки определяет стратегию подбора весов многослойной сети с применением градиентных методов оптимизации. Его

11

необходимым условием выступает дифференцируемость используемых функций активации нейронов сети. Этот алгоритм использует градиентный метод наискорейшего спуска для минимизации среднеквадратической ошибки сети (квадратичной суммы разностей между фактическими и ожидаемыми значениями выходных сигналов),

г) "Машина" опорных векторов (SVM - Support Vector Machine):

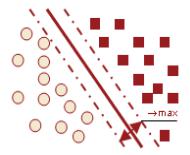
Использует линейное разделение объектов в пространстве признаков с помощью гиперплоскости. Метод применяется для решения задачи бинарной классификации. Основная идея метода опорных векторов — перевод

гиперплоскостями, тем меньше будет средняя ошибка классификатора. Основной проблемой метода является выбор оптимальной гиперплоскости, которая позволяет разделить классы с максимальной точностью. Для этого разделяющая гиперплоскость должна быть выбрана таким образом, чтобы расстояние между ближайшими точками, расположенными по разные стороны от нее, было бы максимальным. Данное расстояние называется зазором, а сами точки – оперными векторами. Тогда разделяющая гиперплоскость должна быть выбрана таким образом, чтобы максимизировать зазор, что обеспечит более уверенное разделение классов;

2) Обучение без учителя (unsupervised learning) - для каждого прецедента задается только "ситуация", требуется сгруппировать объекты в кластеры, используя данные о попарном сходстве объектов, и/или понизить размерность данных; в этом случае ответы не задаются, и требуется искать зависимости между объектами. Задачу можно сформулировать следующим образом: системе одновременно или последовательно предъявляются объекты без каких-либо указаний об их принадлежности к образам. Входное устройство системы отображает множество объектов и, используя некоторое заложенное в нее заранее свойство разделимости образов, производит самостоятельную классификацию этих объектов. После такого процесса самообучения система должна приобрести способность к распознаванию не только уже знакомых объектов (объектов из обучающей последовательности), но и тех, которые ранее не предъявлялись.:

а) Альфа-система подкрепления; б) Гамма-система подкрепления;

в) Метод ближайших соседей (Пример работы метода приведен в Задании 2.1 и Задании 2.2);

3) Обучение с подкреплением (reinforcement learning) - для каждого прецедента имеется пара "ситуация, принятое решение". Роль объектов играют пары «ситуация, принятое решение», ответами являются значения функционала качества, характеризующего правильность принятых решений (реакцию среды). Как и в задачах прогнозирования, здесь существенную роль играет фактор времени. Примеры прикладных задач: формирование инвестиционных стратегий, автоматическое управление технологическими процессами, самообучение роботов, и т.д.:

а) Генетический алгоритм;

12

4)Активное обучение (active learning) - отличается тем, что обучаемый алгоритм имеет возможность самостоятельно назначать следующую исследуемую ситуацию, на которой станет известен верный ответ;

5)Обучение с частичным привлечением учителя (semi-supervised learning) занимает

промежуточное положение между обучением с учителем и без учителя. Каждый прецедент представляет собой пару "объект, ответ", но ответы известны только на части прецедентов. Пример прикладной задачи - автоматическая рубрикация большого количества текстов при условии, что некоторые из них уже отнесены к каким-то рубрикам. Т.е. для части прецедентов задается пара "ситуация, требуемое решение", а для части - только "ситуация";

6)Трансдуктивное обучение (transduction) - обучение с частичным привлечением учителя, когда прогноз предполагается делать только для прецедентов из тестовой выборки;

7)Многозадачное обучение (multi-task learning) - одновременное обучение группе

взаимосвязанных задач, для каждой из которых задаются свои пары "ситуация, требуемое решение". Набор взаимосвязанных или схожих задач обучения решается одновременно, с помощью различных алгоритмов обучения, имеющих схожее внутренне представление. Информация о сходстве задач между собой позволяет более эффективно совершенствовать алгоритм обучения и повышать качество решения основной задачи;

8) Многовариантное обучение (multi-instant learning) - обучение, когда прецеденты могут быть объединены в группы, в каждой из которых для всех прецедентов имеется "ситуация", но только для одного из них (причем, неизвестно какого) имеется пара "ситуация, требуемое решение".

13

Задание 2

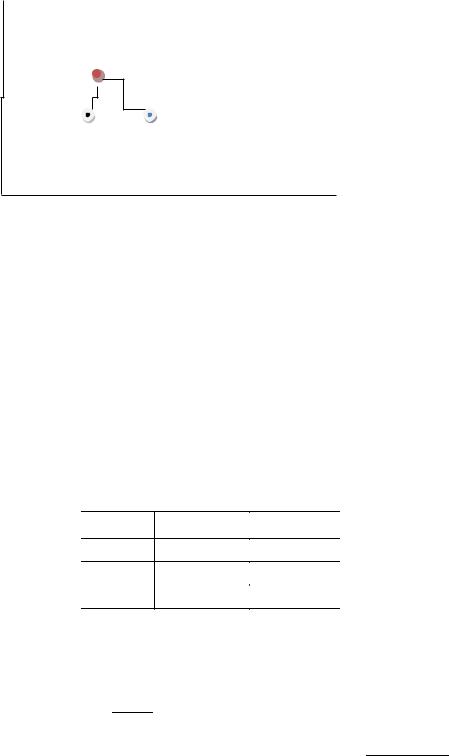
2.1. Задано три образа (вектора информативных признаков): x1 , x2 и x3 . Каждый образ представлен вектором из двух информативных признаков x1 , x2 .

X2

X1

X2

X3

X1

Рис. 1

На Рис.1 показан пример распределения образов в пространстве признаков.

Решение

Задаем значения и заносим их в Таблицу 1:

Таблица 1

Для решения задачи любым из предложенных способов нам понадобятся следующие формулы:

Получим:

14

Ответ: При использовании метрик Евклидова расстояния и направляющих косинусов браз x1 "ближе" к x2 , при использовании метрики расстояния Танимото образ x1 "ближе" к x3 .

2.2. Задана обучающая последовательность, характеризующая некоторое распределение образов на два класса.

Задать произвольно (в диапазоне значений 0 - 10 ) три "своих" образа ( x11 , x12 , x13 ). Определить, к каким классам относятся заданные три вектора.

а) Решить задачу с применением методов ближайшего соседа и сравнения с эталоном (при этом использовать метрику Евклидова расстояния).

б) Решить задачу с использованием метода линейной разделяющей функции и одного из алгоритмов обучения.

Исходные данные и результаты свести в таблицу.

Отобразить распределение образов в Евклидовом пространстве (на плоскости). Сделать выводы

Решение

(при решении задачи будем использовать MS Excel)

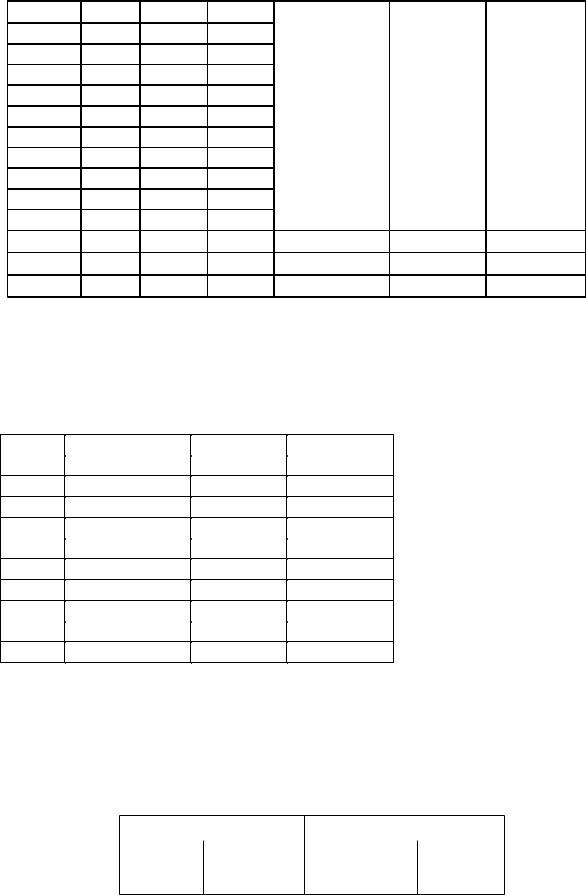
Задаем три "своих" образа и заносим их в Таблицу 1 :

15

Талица 1

а)

Метод ближайшего соседа:

При решении задачи классификации методом ближайшего соседа необходимо каждый "свой" образ сравнивать со всеми образами обучающей последовательности.

Метод сравнения с эталоном:

При решении задачи классификации методом сравнения с эталоном, необходимо сначала вычислить этот эталон (т.е. найти среднее по каждой из координат).

Вычислим эталоны для каждого класса:

Таблица 3

16

Далее для каждого "неклассифицированного" объекта вычислим расстояние до эталона, используя метрику Евклидова расстояния:

Таблица 4

Получаем, что x11 и x13 относятся к классу "1", а x12 к классу "0".

б)

При решении задачи классификации методом линейной разделяющей функции

необходимо «построить» разделяющую линию, т.е. найти коэффициенты w i .

n

∑ wi xi−w0=0 , где

i=1

xi - i-информационный признак;

w i -коэффициент соответствующего признака.

У нас n= 2 , т.е формула гиперплоскости сводится в двухмерном пространстве к прямой w 1 x1 +w2 x2−w 0=0 .

Для нахождения коэффициентов w 1 и w 2 воспользуемся алгоритмом обучения нейронной сети с учителем, основанном на правиле Розенблатта (дельта-правило).

Дельта( )-правило: w i t+1 =w i t +α xi D−Y ,i= 1, . .. ,n , где

i - номер входа.

Алгоритм обучения нейронной сети с учителем:

Инициализируем элементы весовой матрицы небольшими случайными значениями. У нас в матрицу входит два коэффициента w 1 и w 2 . Берём w 1=0,01

и w 2=−0,01 .

Подать на входы один из входных векторов, которые сеть должна научиться различать и вычислить её выходы. Выход вычисляется по формуле

Y=w 1 x1j +w 2 x2j , где x1j и x2j - заданные по условию в таблице координаты образа

17

(вектора) j= 1, .. . ,10 . В нашем случае изначально берем x1 и x2 по порядку из таблицы, т.е. для для образа x1 .

Проверяем равильность выходного сигнала. Правильность проверяется по отношению к эталонному значению D . Выход Y будет считаться правильным, еслиD−Y =0 . Так как идеально получиться не может, нас устроит небольшая

погрешность, т.е. D−Y ≤0,001

модифицируются одновременно. Проделываем модификацию до тех пор, пока нужная нам точность не будет достигнута.

Продолжаем подавать на входы нейронной сети векторы в заданном по условию (в таблице) порядке, но уже используя полученные на шаге 3. значения w 1 и w 2 .

"Прогнав" через входы сети все данные по условию векторы (10 векторов), т.е. обучающую последовательность, мы в итоге получим интересующие нас значения

Занесем найденные коэффициенты в Таблицу 5:

Таблица 5

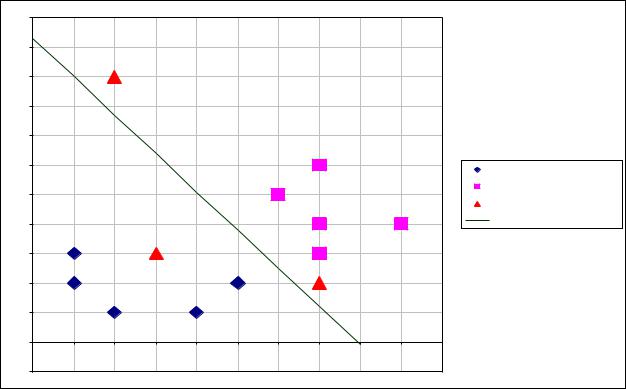
На основе этих коэффициентов, используя формулу w 1 x1 +w2 x2−w 0=0 , построим

разделяющую гиперплоскость на Рис.1. На этом же Рис.1 отобразим распределение образов в Евклидовом пространстве:

18