
Отчеты по лабораторным работам / Лабораторная работа №6
.pdfФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ОБРАЗОВАНИЯ "САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ТЕЛЕКОММУНИКАЦИЙ ИМ. ПРОФ. М. А. БОНЧ-БРУЕВИЧА"
Факультет инфокоммуникационных сетей и систем Кафедра сетей связи и передачи данных
ЛАБОРАТОРНАЯ РАБОТА №6
«Решение многокритериальных задач методом аддитивной оптимизации» по дисциплине
«Оптимизация и математические методы принятия решений» Вариант 10
Выполнил:
студент 2-го курса дневного отделения группы ИКПИ-81 Коваленко Л. А.
Преподаватель:
Владимиров С. А.
Санкт-Петербург
2020
Цель работы
Приобретение навыка постановки и решения многокритериальных задач методом аддитивной оптимизации. Освоение способов нормирования данных.
Постановка задачи
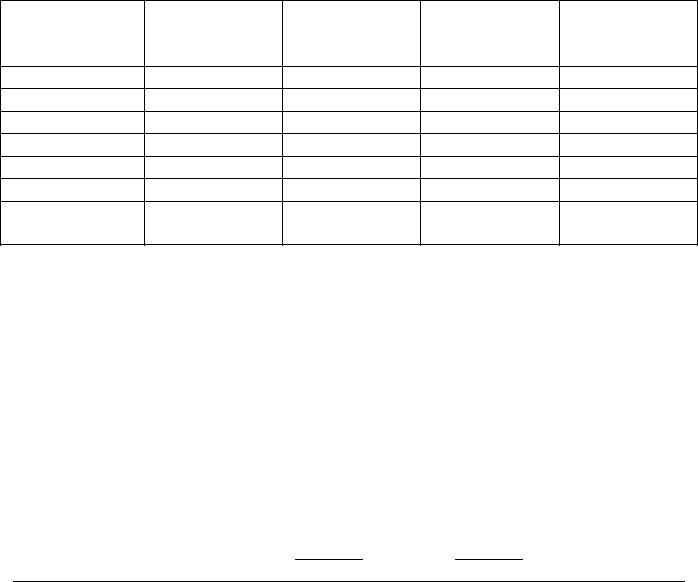
Для семи проектов транспортных устройств определены относительные единичные показатели технологического совершенства конструкции.
Численные значения единичных показателей и соответствующие весовые коэффициенты приведены в таблице:
Варианты |
Прочность |
Перегрузка |
Мощность |
|
транспортных Скорость (К1) |
||||
(К2) |
(К3) |
(К6) |
||
устройств |
||||
|
|
|
1
2
3
4
5
6
Весовые
коэффициенты
Выбрать оптимальное транспортное устройство.
|
|
|
+ |
= max , |
|
Ход работы |
|
|
|
|
|
|
|
|
= 1 … |
|||||||||
1. |
|
|
|
− = min , |
|
|
|
|
||||||||||||||||
Определение максимума и минимума каждого |
частного критерия: |
|||||||||||||||||||||||
2. |
При |
|
1+ |
= 1.2, |
|
2+ |
= 1.0, |
3+ |
= 1.0, |
|
|
4+ = 1.0 |
||||||||||||
1 = 0.87, |
2 |
= 0.78, |
3 |
= 0.65, |
|
|
|
4 = 0.77 |
||||||||||||||||
|
|
− |
|
|
|
− |
|
|
|
|
|
− |
|
|
|
|
|
|
|
|
|
− |
||
|
|
решении |
задачи |
|
максимизируются |
|
первый |
|
(скорость), второй |
|||||||||||||||
|
(прочность) и четвертый (мощность) |
критерии, |
|
а минимизируется третий |
||||||||||||||||||||
3. |
(перегрузка). |
|
1 |
= |
1 |
− 1 |
, |
2 |
= |
2 |
− 2 |
|
, |
|
|
|||||||||
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
1+ |
− 1− |
2+ |
− 2− |
|
|
||||||||||||||||
Нормализация критериев: |
|
− |
|
|
|
|
4 |
|
− |
|
|
|
||||||||||||
|
|
|
|
|
|
|
3 |
− 3 |
|
|
|
|
− 4 |
|||||||||||
|
|
|
|
3 |
= |
+ |
|
|
|
, |
4 |
= |
|
+ |
|
|
− |
|||||||
|
|
|
|
|
+ |
|
|
− |
|
|
|
− |
|
|
||||||||||
|
11 |
|
|
12 |
|
|
3 |
− |
|
3 |
|
13 |
|
|
4 |
|
− 4 |
|
14 |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
21 |
|
|
22 |
|
|
|
|
|
|
|
|
23 |
|
|
|
|
|
|
|
|
24 |
|
|
|
31 |
|
|
32 |
|
|
|
|
|
|
|
|
33 |
|
|
|
|
|
|
|
|
34 |
|
|
|
41 |
|
|
42 |
|
|
|
|
|
|
|
|
43 |
|
|
|
|
|
|
|
|
44 |
|
|
|
51 |
|
|
52 |
|
|
|
|
|
|
|
|
53 |
|
|
|
|
|
|
|
|
54 |
|
|
|
61 |
|
|
62 |
|
|
|
|
|
|
|
|
63 |
|
|
|
|
|
|
|
|
64 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|

4. Определение обобщенной функции цели по каждому варианту:
1 |
1 |
11 |
2 |
12 |
3 |
13 |
4 |
14 |
|
|
|
|
= 0.09823 |
|
|
|
|
|
||||
2 |
1 |
21 |
2 |
22 |
3 |
23 |
4 |
24 |
|
|
|
|
|
|
|
|
|
|||||
3 |
1 |
31 |
2 |
32 |
3 |
33 |
4 |
34 |
|
|
|
|
= 0.88777 |
|
|
|
|
|
||||
4 |
1 |
41 |
2 |
42 |
3 |
43 |
4 |
44 |
|
|
|
|
= 0.59565 |
|
|
|
|
|
||||
5 |
1 |
51 |
2 |
52 |
3 |
53 |
4 |
54 |
|
|
|
|
= 0.40171 |
|
|
|
|
|
||||
6 |
1 |
61 |
2 |
62 |
3 |
63 |
4 |
64 |
|
|
|
|
= 0.32797 |
|
|
|
|
|
||||
|
Ответы на вопросы: |
|
2-ый |
= 0.65822 |
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
= 2 = 0.88777 |
|
|
|
|
||||||||||||
|
|
Оптимальным является |
|
|
|
|
вариант транспортного устройства, так как |
|||||||||||||||
|
1. |
Математическая модель задач принятия решений в условиях |
||||||||||||||||||||
|
|
|
определенности задается в виде таблиц, элементами которых являются |
|||||||||||||||||||
|
|
|
значения частных критериев эффективности функционирования системы, |
|||||||||||||||||||
|
|
|
вычисленные для каждой из сравниваемых стратегий при строго заданных |
|||||||||||||||||||
|
|
|
внешних условиях, параметры значимых величин и другие условия. |
|||||||||||||||||||
|
2. |
Многокритериальная задача — задача, в которой производится выбор |
||||||||||||||||||||
|
|
|
оптимального решения по комплексу нескольких стратегически важных или |
|||||||||||||||||||
|
|
|
значимых критериев. |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
3. |
Методы свертывания критериев в многокритериальных задачах: |
||||||||||||||||||||
|
|
|
• |
Аддитивная свертка. |
|
|
|
|
|
|
|
|||||||||||
|
|
|
• |
Мультипликативная свертка. |
|
|
|
|
|
|||||||||||||
|
4. |
Метод аддитивной оптимизации заключается в весовом суммировании |
||||||||||||||||||||
|
|
|
значений критериев. |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
5. |
Весовой коэффициент — это параметр, который отражает значимость |
||||||||||||||||||||
|
|
|
данного критерия или показателя по сравнению с другими критериями. |
|||||||||||||||||||
|
6. |
Где |
|
|
|
= =1 |
|
|
, |
|
|
= 1 … , |
=1 |
= 1, |
|
≥ 0 |
||||||
|
Обобщенная функция в методе аддитивной оптимизации: |
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
— частные критерии, |
— весовые коэффициенты. |
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||
7.Алгоритм нормализации критериев:
1)Определение максимума и минимума каждого частного критерия.
2)Выделение группы критериев, которые максимизируются при решении задачи, и группу критериев, которые минимизируются при решении задачи.
3)Оптимальнымбудеттот вариант,который обеспечиваетмаксимальное (в соответствии с принципом максимальной эффективности) или
минимальное (в соответствии с принципом минимальной потери)
значение целевой функции: = max(min) =1
3
