1.3. Решение дифференциальных уравнений операционным методом
При решении линейных дифференциальных уравнений с постоянными коэффициентами операционным методом необходимо:
1. Используя свойства преобразования Лапласа перевести уравнение в пространство изображений.
2.
Найти из полученного алгебраического
уравнения изображение
искомой функции.
3.
Выполнив обратное преобразование
Лапласа, найти
.
При решении систем дифференциальных уравнений вместо одного операторного уравнения получим систему линейных алгебраических уравнений относительно изображений искомых функций, а затем найдем их оригиналы.
Пример
5.
Найти решение дифференциального
уравнения , удовлетворяющее начальным
условиям:
.
Решение.
Пусть
,
тогда
.
Операторное уравнение будет иметь вид:
.
Отсюда
.
Найдем оригиналы для каждого слагаемого:
,
(по свойству 6).
Следовательно,
.
1.4. Решение линейных дифференциальных уравнений с помощью формулы Дюамеля
В прикладных задачах электротехники и радиотехники нередко приходится находить отклики системы на различные сигналы, т.е. многократно решать дифференциальные уравнения с одной и той же левой частью. Если начальные условия нулевые, то в этом случае рекомендуется найти отклик системы на единичный сигнал , а затем все остальные решения получать по формуле Дюамеля
.
(1.7)
Пример
6.
Решить дифференциальное уравнение ,
если
.
Решение. Составим вспомогательное уравнение, заменив правую часть единичной функцией:
Пусть
,
тогда операторное уравнение будет иметь
вид:
.
Отсюда
.
По формуле (1.7) получаем решение исходного уравнения:
Заметим, что этот же способ используется, если возникают трудности при нахождении изображения для правой части дифференциального уравнения.
2. Расчетные задания
Задача
1. Найти изображения функций и
,
если:
|
1.1.
|
1.2. . |
|
1.3.
|
1.4.
|
|
1.5.
|
1.6.
|
|
1.7. . |
1.8. . |
|
1.9. . |
1.10. . |
|
1.11. . |
1.12. . |
|
1.13. |
1.14. . |
|
1.15. . |
1.16. . |
|
1.17. |
1.18.
|
|
1.19.
|
1.20. . |
|
1.21. . |
1.22.
|
|
1.23.
|
1.24.
|
|
1.25.
|
|
.
.
.
.
.
.
.
.
.
.
.
.
Задача 2. Найти изображение функции, заданной графически.
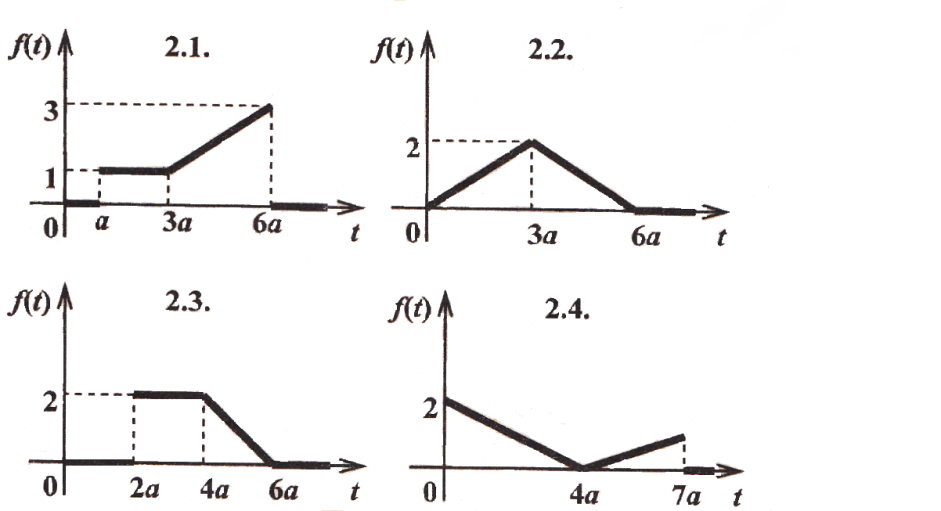
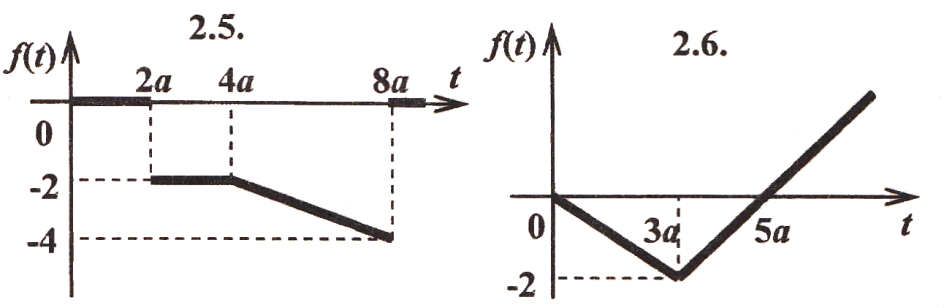
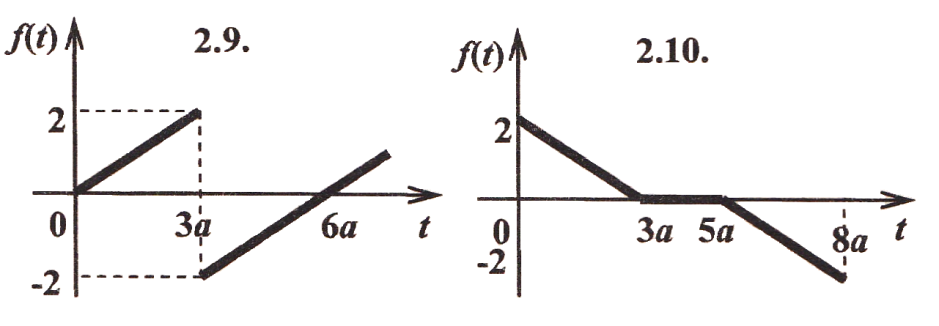
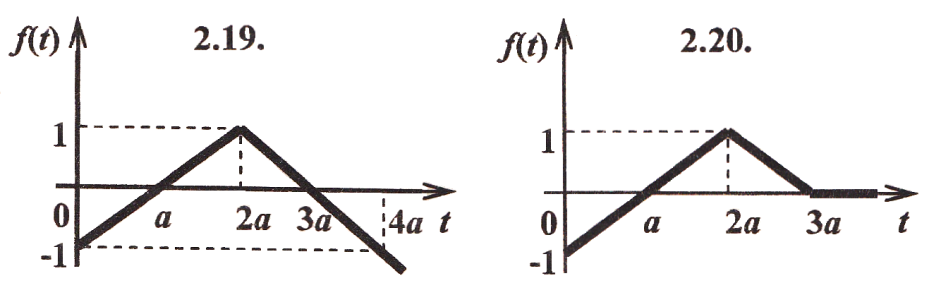
Задача
3. Функция
при
равна нулю, а при
является периодической. Построить
график этой функции и найти её изображение.
-
3.1.
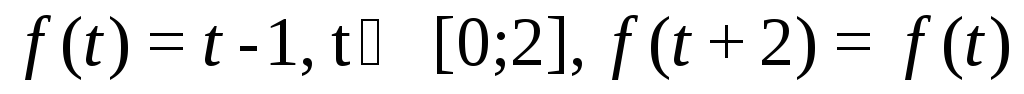.3.2.
.3.3.
.3.4.
.3.5.
.3.6.
.3.7.
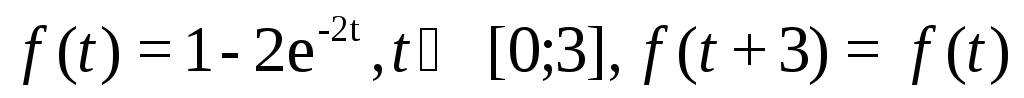.3.8.
.3.9.
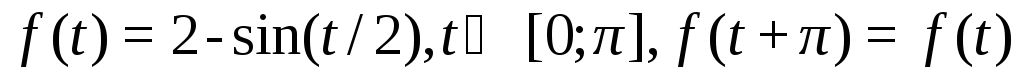.3.10.
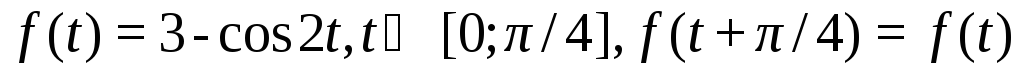.3.11.
.3.12.
.3.13.
.3.14.
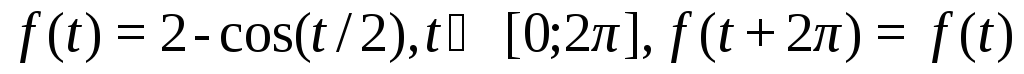.3.15.
.3.16.
.3.17.
.3.18.
.3.19.
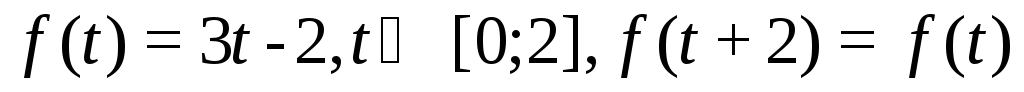.3.20.
.3.21.
.3.22.
.3.23.
.3.24.
.3.25.
.
Задача 4. С помощью вычетов найти оригинал по заданному изображению. Ответ записать в действительной форме.
|
4.1. |
4.2. |
|
4.3. |
4.4. |
|
4.5. |
4.6.
|
|
4.7.
|
4.8.
|
|
4.9.
|
4.10.
|
|
4.11.
|
4.12.
|
|
4.13.
|
4.14.
|
|
4.15.
|
4.16.
|
|
4.17.
|
4.18.
|
|
4.19.
|
4.20.
|
|
4.21.
|
4.22.
|
|
4.23.
|
4.24.
|
|
4.25.
|
|
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
Задача 5. Найти оригинал по заданному изображению.
|
5.1.
|
5.2.
|
|
5.3.
|
5.4.
|
|
5.5.
|
5.6.
|
|
5.7.
|
5.8.
|
|
5.9.
|
5.10.
|
|
5.11.
|
5.12.
|
|
5.13.
|
5.14.
|
|
5.15.
|
5.16.
|
|
5.17.
|
5.18.
|
|
5.19.
|
5.20.
|
|
5.21.
|
5.22.
|
|
5.23.
|
5.24.
|
|
5.25.
|
|
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
Задача 6. Операционным методом решить дифференциальное уравнение при заданных начальных условиях.
|
6.1.
|
|
6.2.
|
|
6.3.
|
|
6.4.
|
|
6.5.
|
|
6.6.
|
|
6.7.
|
|
6.8.
|
|
6.9.
|
|
6.10.
|
|
6.11.
|
|
6.12.
|
|
6.13.
|
|
6.14.
|
|
6.15.
|
|
6.16.
|
|
6.17.
|
|
6.18.
|
|
6.19.
|
|
6.20.
|
|
6.21.
|
|
6.22.
|
|
6.23.
|
|
6.24.
|
|
6.25.
|
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
Задача
7. По формуле Дюамеля (1.7) найти решения
дифференциальных уравнений, удовлетворяющих
условиям
.
|
7.1.
|
|
7.2.
|
|
7.3.
|
|
7.4.
|
|
7.5.
|
|
7.6.
|
|
7.7.
|
|
7.8.
|
|
7.9.
|
|
7.10.
|
|
7.11.
|
|
7.12.
|
|
7.13.
|
|
7.14.
|
|
7.15.
|
|
7.16.
|
|
7.17.
|
|
7.18.
|
|
7.19.
|
|
7.20.
|
|
7.21.
|
|
7.22.
|
|
7.23.
|
|
7.24.
|
|
7.25.
|
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
Задача 8. Решить систему дифференциальных уравнений операционным методом.
|
8.1.
|
8.2.
|
|
8.3.
|
8.4.
|
|
8.5.
|
8.6.
|
|
8.7.
|
8.8.
|
|
8.9.
|
8.10.
|
|
8.11.
|
8.12.
|
|
8.13.
|
8.14.
|
|
8.15.
|
8.16.
|
|
8.17.
|
8.18.
|
|
8.19.
|
8.20.
|
|
8.21.
|
8.22.
|
|
8.23.
|
8.24.
|
|
8.25.
|
|
Задача 9. Электрическая цепь, состоящая из резистора (сопротивление R), конденсатора (емкость C) и катушки индуктивности (индуктивность L), соединенных последовательно, включается на постоянную э.д.с. E. В начальный момент времени заряд и ток равны нулю. Найти зависимость тока в цепи от времени I(t).
9.1. R=27 Ом, C=30 пФ, L=20 мкГн, E=1,2 В.
9.2. R=50 Ом, C=40 пФ, L=20 мкГн, E=1,5 В.
9.3. R=3 Ом, C=8 мкФ, L=7 мГн, E=2,4 В .
9.4. R=15 Ом, C=10 мкФ, L=7 мГн, E=3 В.
9.5. R=25 Ом, C=50 пФ, L=20 мкГн, E=6 В.
9.6. R=50 Ом, C=60 пФ, L=20 мкГн, E=9 В.
9.7. R=7 Ом, C=12 мкФ, L=7 мГн, E=1,2 В.
9.8. R=12 Ом, C=15 мкФ, L=7 мГн, E=1,5 В.
9.9. R=12 Ом, C=30 пФ, L=25 мкГн, E=2,4 В.
9.10. R=60 Ом, C=40 пФ, L=25 мГн, E=3 В.
9.11. R=10 Ом, C=8 мкФ, L=10 мГн, E=6 В.
9.12. R=15 Ом, C=10 мкФ, L=10 мГн, E=9 В.
9.13. R=18 Ом, C=25 пФ, L=25 мкГн, E=1,2 В.
9.14. R=65 Ом, C=60 пФ, L=25 мкГн, E=1,5 В.
9.15. R=12 Ом, C=12 мкФ, L=10 мГн, E=2,4 В.
9.16. R=20 Ом, C=15 мкФ, L=10 мГн, E=3 В.
9.17. R=22 Ом, C=30 пФ, L=30 мкГн, E=9 В.
9.18. R=55 Ом, C=40 пФ, L=30 мкГн, E=9 В.
9.19. R=14 Ом, C=60 пФ, L=20 мкГн, E=12 В.
9.20. R=20 Ом, C=10 мкФ, L=15 мГн, E=1,5 В.
9.21. R=25 Ом, C=50 пФ, L=30 мкГн, E=3 В.
9.22. R=40 Ом, C=60 пФ, L=27 мкГн, E=3 В.
9.23. R=7 Ом, C=12 мкФ, L=15 мГн, E=6 В.
9.24. R=14 Ом, C=15 мкФ, L=15 мГн, E=12 В.
9.25. R=3 Ом, C=8 мкФ, L=15 мГн, E=1,2 В.
Задача
10. В цепи, состоящей из самоиндукции L
и ёмкости C,
включенных последовательно, в момент
времени
приложена электродвижущая сила
.
В начальный момент времени . Найти I(t),
Выяснить при каких условиях в контуре возникает резонанс.
Содержание
1.1. Прямое преобразование Лапласа…………………2
1.2. Обратное преобразование Лапласа…………....…6
1.3.Решение дифференциальных уравнений операционным методом ………………………………8
1.4. Решение линейных дифференциальных
уравнений с помощью формулы Дюамеля…………...9
2. Расчетные задания………………………......……...10