В предлагаемых методических указаниях рассматривается операционный метод решения обыкновенных линейных дифференциальных уравнений, который следует использовать при выполнении курсовой работы. Такими уравнениями описываются многие физические процессы в задачах прикладной математики, радиотехники и электротехники. Классический способ решения этих дифференциальных уравнений, рассмотренный нами ранее, обычно используется в электротехнике только при расчёте переходных процессов в линейных цепях второго порядка сложности [3]. Для электрических цепей более высокого порядка сложности он практически не применяется, так как расчёты очень трудоёмки из-за необходимости вычисления большого числа постоянных по заданным начальным условиям. В этом случае целесообразно использовать операционный метод решения уравнений, при котором начальные условия учитываются при переходе от дифференциальных уравнений к алгебраическим.

Этот метод заключается в том, что с помощью свойств Лапласа все функции, входящие в дифференциальные уравнения, из пространства оригиналов переводятся в пространство изображений. Операции, которые выполняются с оригиналами (например дифференцирование, интегрирование), в пространстве изображений существенно упрощаются, поэтому линейное дифференциальное уравнение любого порядка преобразуется в линейное алгебраическое уравнение, а система линейных дифференциальных уравнений — в линейную систему алгебраических уравнений. Из этих уравнений находят изображения искомых функций, а затем с помощью обратного преобразования Лапласа сами функции, которые являются решениями задачи Коши для заданных дифференциальных уравнений.

При выполнении курсовой работы студенту следует изучить необходимый теоретический материал, изложенный в первом разделе и в учебных пособиях [1]-[4], и разобраться в решении типовых примеров. Затем в соответствии со своим порядковым номером в списке группы выбрать вариант и из второго раздела выписать задачи, соответствующие этому варианту.

1. Операционное исчисление

1.1. Прямое преобразование Лапласа

Преобразованием Лапласа функции действительного переменного называется функция комплексного переменного , определяемая формулой

. (1.1)

Функция называется оригиналом и должна удовлетворять условиям:

1) — кусочно-непрерывная однозначная функция ;

2) ;

3) .

Эти условия обеспечивают абсолютную сходимость несобственного интеграла (1.1) в полуплоскости .

Функцию называют изображением для , она является аналитической в области . Соответствие между оригиналом и его изображением обозначают символически или . Для нахождения изображений наряду с формулой (1.1) могут быть использованы следующие свойства:

1. Линейность. Если , , то , где — любые комплексные постоянные.

2. Теорема подобия. Если , то.

3. Смещение изображения. Если , то , где —любое комплексное число.

4. Запаздывание оригинала. Если , то для любого . Здесь — единичная функция Хэвисайда, которая равна 1 при и нулю при .

5. Дифференцирование оригинала. Если функции являются оригиналами и , то

,

……………………….. (1.2)

6. Дифференцирование изображения. Если , то

,

……………….…….

.

7. Интегрирование оригинала. Если , то

.

8. Интегрирование изображения. Если и является оригиналом, то .

9. Изображение периодической функции. Если , где и , а — периодическая функция , то

. (1.3)

10. Умножение изображений. Если , , а и непрерывны на промежутке , то

. (1.4)

11. Формула Дюамеля. Если , , то

Таблица основных операционных соотношений

№	1	2	3	4	5	6
		t

7	8	9	10	11

Пример 1. Найти изображения функций и , если .

Решение. Преобразуем функцию к виду:

Используя свойства 1 и 3 и таблицу изображений, получаем

По формуле (1.2) имеем:

.

Пример 2. Найти изображение периодической функции (рис. 1)

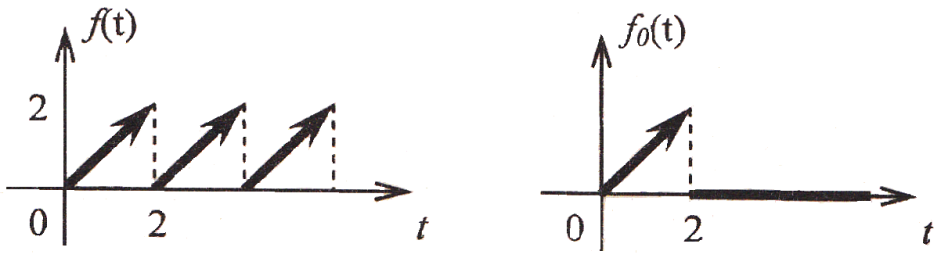
Рис. 1. Рис. 2.

Решение. Очевидно и Т=2, тогда (рис. 2)

Применяя теорему запаздывания, получим:

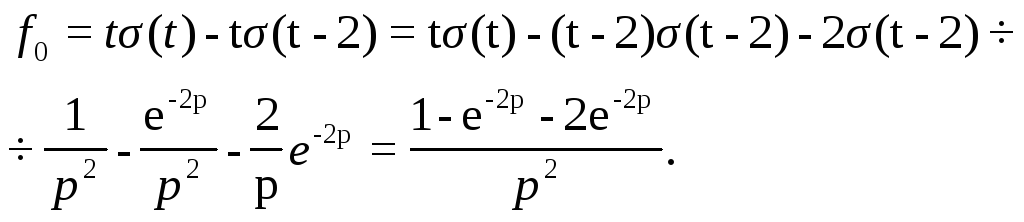
По формуле 1.3 имеем

.

1.2. Обратное преобразование Лапласа

Рассмотрим теперь обратную задачу: по известному изображению будем находить оригинал. Сделать это по формуле обращения

крайне затруднительно, поэтому при отыскании оригиналов следует использовать таблицу изображений, свойства преобразования Лапласа и теорему разложения: если — изолированные особые точки дробно-рационального изображения , то оригинал находится по формуле

. (1.5)

При этом в полюсе кратности “n” вычеты вычисляются по формуле

(1.6)

а в простом полюсе

. (1.7)

В этом случае, если все особые точки являются простыми полюсами, то (1.5) принимает вид [2]

. (1.8)

Пример 3. Найти оригинал для изображения

.

Решение. Приравняв нулю знаменатель найдем три изолированные особые точки: . Все они являются простыми полюсами поэтому воспользуемся формулой (1.8), предварительно вычислив . Тогда

.

Пример 4. Найти оригинал изображения

.

Решение. Применяя теорему умножения получим:

.
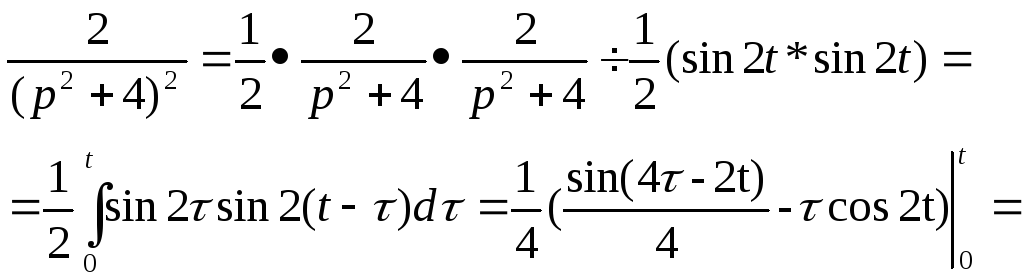