Введение

Самостоятельная работа студентов играет важнейшую роль в успешном изучении курса высшей математики. В течение первых двух семестров эта работа включала в себя регулярное выполнение домашних заданий по темам, изучаемым на практических занятиях, выполнение индивидуальных домашних заданий (типовых расчетов) с последующей защитой результатов, самостоятельное изучение некоторых теоретических вопросов из программы курса и т.д. В третьем семестре к этим видам работы добавляется курсовая работа, на выполнение которой потребуется затратить достаточно много времени, поэтому заниматься ею следует с начала семестра.

В настоящих методических указаниях даются рекомендации по грамотному выполнению и оформлению этой работы. Целью курсовой работы является изучение операционного метода решения линейных неоднородных дифференциальных уравнений и систем уравнений и применение этого метода для анализа переходных процессов в линейных электрических цепях второго порядка сложности.

Анализ переходных процессов практически сводится к решению соответствующих дифференциальных уравнений и может быть выполнен классическим способом с использованием характеристического уравнения и метода неопределённых коэффициентов при подборе частного решения по заданной правой части уравнения. Однако в этом случае необходимо решить две системы линейных алгебраических уравнений: одна составляется для отыскания неизвестных коэффициентов в частном решении, а вторая — для отыскания произвольных постоянных по заданным начальным условиям.

Большим преимуществом операционного метода решения дифференциальных уравнений является то, что начальные условия используются сразу при переводе уравнения в пространство изображений и никаких алгебраических систем решать не приходится. Это значительно упрощает вычисления, поэтому операционный метод активно используется в различных прикладных задачах.

Задание к курсовой работе

1. В соответствии со своим порядковым номером в журнале выбрать из раздела “Расчетные задания” [1] вариант.

2. Изучить основные свойства преобразования Лапласа и их использование при решении линейных неоднородных дифференциальных уравнений и систем уравнений [1], [2], [3].

3. В задачах 1-5 выполнить прямое и обратное преобразования Лапласа.

4. В задачах 6, 7, 8 операционным методом решить дифференциальные уравнения и систему заданных дифференциальных уравнений.

5. В задачах 9, 10 построить схемы электрических контуров [4], составить дифференциальные уравнения для тока и решить их операционным методом. В десятой задаче выяснить, при каких условиях в контуре возникает резонанс.

Этапы выполнения курсовой работы

Курсовая работа должна выполняться по этапам. Сроки выполнения и представления результатов устанавливаются преподавателем.

Первый этап — выбор своего варианта и изучение необходимого теоретического материала.

Второй этап — выполнение прямого и обратного преобразований Лапласа в первых пяти задачах. Отметим наиболее типичные ошибки, допускаемые при выполнении этих заданий. Так, при отыскании изображения для произведения функций ошибочно предполагается, что изображение будет равно произведению изображений . Однако из теоремы умножения [1] следует, что оригиналом для произведения является не произведение , а свёртка этих функций:

Поэтому произведение следует предварительно преобразовать в сумму или разность функций и только после этого искать изображение.

Пример 1. Найти изображение функции

Решение. С помощью известных тригонометрических формул преобразуем функцию к виду:

а затем применим свойство линейности изображений:

Пример 2. Найти изображение функции .

Решение. Предварительно преобразуем функцию к виду:

а затем применим свойство линейности:

При выполнении обратного преобразования в некоторых случаях, если в условии задачи нет требования о применении вычетов, можно с помощью тождественных преобразований представить заданную функцию в виде суммы слагаемых, для каждого из которых оригинал можно найти по таблице.

Пример 3. Найти оригинал для функции

Решение. Поскольку эта функция при имеет полюс четвёртого порядка, то при нахождении оригинала с помощью вычетов функцию необходимо три раза дифференцировать, что достаточно трудоёмко. Поэтому выполним предварительно некоторые тождественные преобразования, а затем воспользуемся таблицей изображений

Третий этап — решение дифференциальных уравнений (задачи 6-7) и системы дифференциальных уравнений (задача 8).

В предлагаемых уравнениях и системах все коэффициенты и правые части уравнений действительны, поэтому ответ следует записать в действительной форме, применив в случае необходимости формулы Эйлера:

Пример 4. Решить дифференциальное уравнение при начальных условиях

Решение. Пусть , тогда [1] , , а . В пространстве изображений получаем уравнение

.

Отсюда

Эта функция имеет три простых полюса , . Производная знаменателя Вычислив оригинал с помощью вычетов [1], получим:

Применив формулы Эйлера и приведя дроби, стоящие в скобках к общему знаменателю, имеем:

.

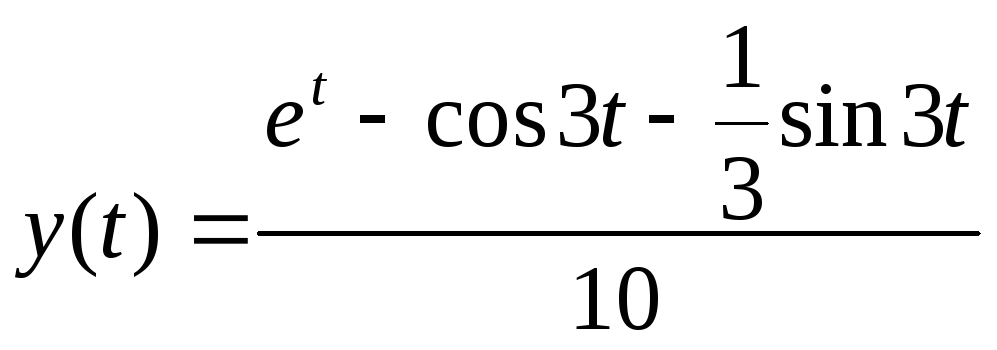Полученные при решении дифференциальных уравнений ответы рекомендуется проверить, подставив найденную функцию y(t) в начальные условия и в заданное дифференциальное уравнение. Это позволит самостоятельно обнаружить ошибки, исправить их до представления отчёта преподавателю и избежать снижения оценки за курсовую работу.

Заметим, что все проверочные действия выполняются для самоконтроля и их не следует включать в отчёт.

Четвёртый этап — составление дифференциальных уравнений для тока в задачах 9 и 10 и их решение. При составлении уравнений следует указать, какие физические законы при этом используются [4], особое внимание следует уделить постановке начальных условий. Одно из них задано в условии задачи, а следует найти.

Пятый этап — оформление отчёта и представление его преподавателю.

Отчёт оформляется на стандартных листах белой бумаги с соблюдением требований нормо-контроля. В отчёт следует включить используемые теоретические сведения и аккуратно оформленные решения практических заданий.

Кроме этого отчёт обязательно должен содержать: титульный лист (см. приложение А), задание на курсовую работу, содержание (перечисление разделов с указанием страниц) и список используемых литературных источников.

В заключение приведём примерный образец оформления расчётных заданий двадцать пятого варианта из курсовой работы, которую выполнил студент группы РК-122 Шишлин М (Приложение Б).

БИБЛИОГРАФИЧЕСКИЙ СПИСОК

1. Пискунов Н.С. Дифференциальное и интегральное исчисления. М., 1985. Т. 2.

2. Кретова Л.Д., Ускова Н.Б., Посметьев В.В. Дифференциальные уравнения. Функции комплексного переменного: учебное пособие. Воронеж: ГОУВПО «Воронежский государственный технический университет», 2007.

3. Матвеев Б.В. Общая электротехника и электроника. Ч. 2. Переходные процессы и спектры: учебное пособие. Воронеж: ГОУВПО «Воронежский государственный технический университет», 2007.

Приложение А. Образец титульного листа

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ

РОССИЙСКОЙ ФЕДЕРАЦИИ

ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО

ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ

«ВОРОНЕЖСКИЙ ГОСУДАРСТВЕННЫЙ

ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ»

(ФБГОУ ВПО «ВГТУ»)

Факультет информационных технологий и компьютерной безопасности

Кафедра высшей математики и физико-математического моделирования

Курсовая работа

по дисциплине «Математика»

Тема:«Операционный метод анализа электрических цепей»

Вариант 1

Выполнил студент группы ПС 121 _________Носова Л.А.

Руководитель доцент каф. ВМФММ ________Ускова Н.Б.

Защищена _________ ___________

дата оценка

Воронеж 2013

Приложение Б. Образец выполнения курсовой работы

ЗАДАНИЕ НА КУРСОВУЮ РАБОТУ

1. Изложить основные свойства преобразования Лапласа, доказав теорему об изображении периодических оригиналов и о дифференцировании оригиналов.

2. Выполнить прямое и обратное преобразование Лапласа в задачах № 1-5.

3. Операционным методом решить заданные дифференциальные уравнения и систему уравнений в задачах № 6-8.

4. Построить схему электрических контуров в задачах № 9, 10. Составить дифференциальные уравнения для тока и решить их операционным методом. В задаче № 10 выяснить при каких условиях в контуре возникает резонанс.

Содержание

1. Прямое преобразование Лапласа	4
2. Обратное преобразование Лапласа	6
3. Теорема об изображении периодических оригиналов	6
4. Теорема о дифференцировании оригиналов	7
5. Расчетные задания	8

1. Прямое преобразование Лапласа

Преобразованием Лапласа функции действительного переменного называется функция комплексного переменного , определяемая формулой

. (1)

Функция называется оригиналом и должна удовлетворять условиям:

1) кусочно-непрерывная однозначная функция

2)

3) .

Эти условия обеспечивают абсолютную сходимость несобственного интеграла (1.1) в полуплоскости Re.

Функцию называют изображением для , она является аналитической в области Re. Соответствие между оригиналом и его изображением обозначают символически или .

Для нахождения изображений наряду с формулой (1) могут быть использованы следующие свойства:

1. Линейность. Если то

где – любые комплексные постоянные.

2. Теорема подобия. Если , то .

3. Смещение изображения. Если , то , где – любое комплексное число.

4. Запаздывание оригинала. Если , то для любого . Здесь – единичная функция Хэвисайда, которая равна 1 при и 0 при .

5. Дифференцирование изображения. Если , то

…..………

.

6. Интегрирование оригинала. Если , то .

7. Интегрирование изображения. Если и является оригиналом, то .

8. Умножение изображений. Если , а и непрерывны на промежутке , то

(2)

9. Формула Дюамеля. Если , то

2. Обратное преобразование Лапласа

Рассмотрим теперь обратную задачу: по известному изображению будем находить оригинал . Сделать это по формуле обращения

крайне затруднительно, поэтому при отыскании оригиналов следует использовать таблицу изображений, свойства преобразования Лапласа и теорему разложения: если – изолированные особые точки дробно-рационального изображения , то оригинал находится по формуле

. (3)

Заметим, что если и все особые точки являются простыми полюсами, то:

(4)

3. Теорема об изображении периодических оригиналов

Теорема: Если , где и , а – периодическая функция , то

. (5)

Доказательство: Представим изображение функции в виде суммы интегралов:

Первый интеграл оставим без изменений, во втором выполним подстановку , в третьем интеграле возьмем подстановку . Получим:

Так как по условию нам дано, что функция периодическая, то . Вынесем за знак интеграла множители, которые не нужно интегрировать. Получим:

Но при , следовательно:

Тогда

Выражение, стоящее в скобках является бесконечно убывающей геометрической прогрессией со знаменателем , сумма которой равна , следовательно , что и требовалось доказать.

4. Теорема о дифференцировании оригиналов

Теорема: Если функции …, являются оригиналами и , то

,

,

………………… (6)

Доказательство: Согласно формуле (1) , тогда

.

Вычислив этот интеграл по частям, и учитывая, что , получим:

тогда

Аналогичным образом получаем формулу для n-ой производной:

.

5. Расчетные задания

Задача 1. Найти изображение функций и , если

Используя свойство 5 и таблицу изображений, получаем:

.

Применив свойство о смещении изображения, получим:

.

По формуле (6) имеем:

.

Задача 2. Найти изображение функции, заданной графически.

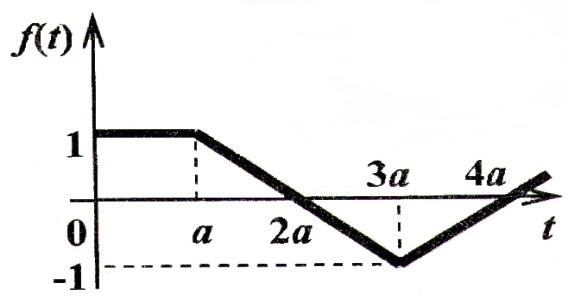
Составим уравнения наклонных прямых. Уравнение первой прямой имеет вид:

Уравнение второй прямой имеет вид:

.

Таким образом, будет иметь аналитически заданную функцию:

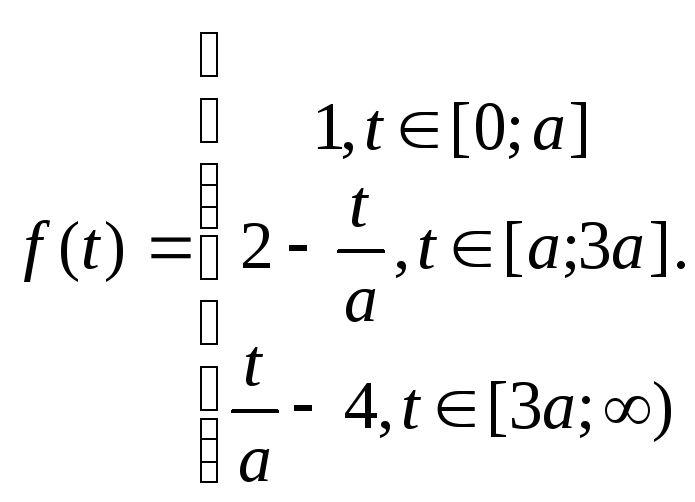
Используя функцию Хэвисайда, запишем в виде:

Применяя свойство 4 о запаздывании оригинала, получим:

Задача 3. Функция при равна нулю, а при является периодической:

Найдем изображение данной функции. По формуле (5) прямого преобразования Лапласа мы имеем:

.

По формуле (1) найдем:

Из тригонометрии мы знаем, что , тогда преобразуем изображение к следующему виду:

.

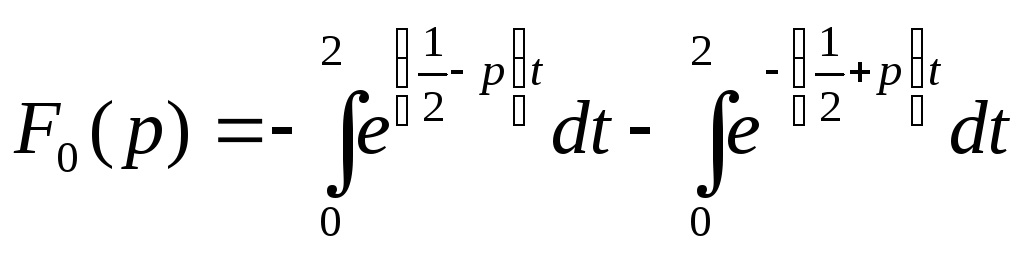После вычисления определённых интегралов и подстановки пределов получим:

По формуле (3) имеем:

Задача 4. С помощью вычетов найти оригинал для изображения Ответ записать в действительной форме.

Найдем особые точки данной функции. Для этого приравняем знаменатель функции к 0:

Получим 3 полюса: Во всех 3 случаях кратность полюсов равна 1.

По формуле (4) будем иметь:

Задача 5. Найти оригинал по заданному изображению

Преобразуем данное изображение к следующему виду:

Пусть , тогда Найдем особые точки функции . Для этого приравняем знаменатель функции к 0:

Получим 2 полюса: . Кратность первого полюса кратность второго .

По формуле (3) будем иметь:

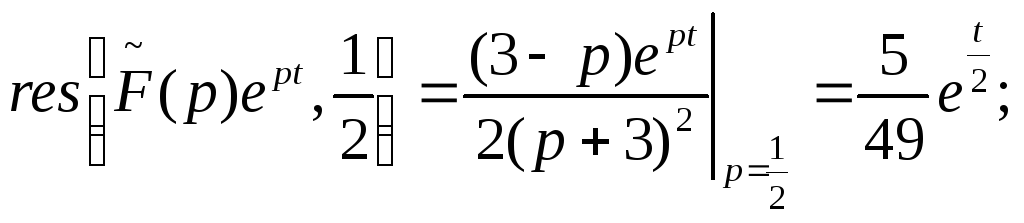
После сложения вычетов получим:

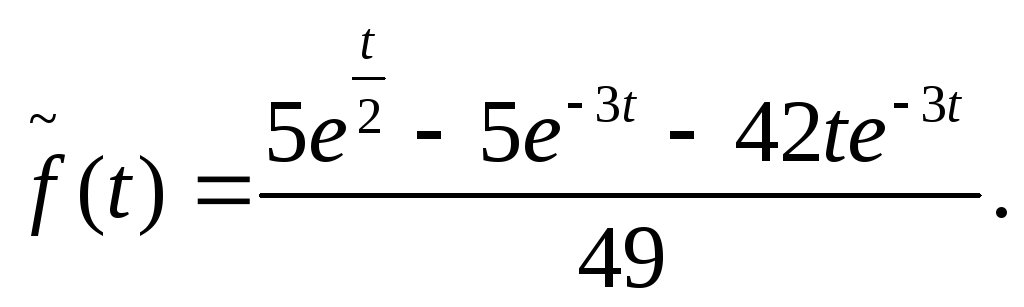
По свойству о запаздывании оригинала получаем:

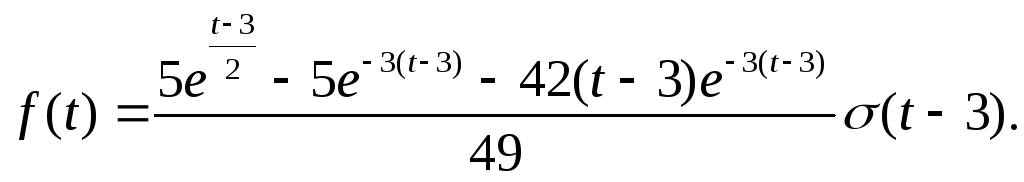
Задача 6. Операционным методом решить дифференциальное уравнение при заданных начальных условиях .

Пусть , тогда по формуле (2) получим:

Операторное уравнение будет иметь вид:

Выразим из данного уравнения :

Найдем особые точки данного изображения. Для этого приравняем знаменатель к 0:

Получим два полюса и . Кратность обоих полюсов равна двум.

По формуле (3) будем иметь:

Суммируя вычеты и применяя формулу Эйлера, получим:

Задача 7. По формуле Дюамеля найти решения дифференциальных уравнений , удовлетворяющих условиям .

Составим вспомогательное уравнение, заменив правую часть единичной функцией Хэвисайда:

Пусть , тогда по формуле (2) получим:

Операторное уравнение будет иметь вид:

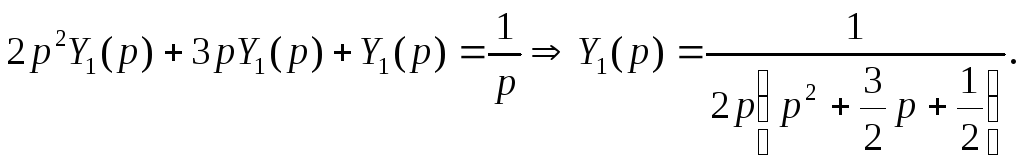
Найдем особые точки данного изображения. Для этого приравняем знаменатель к 0:

Получим три полюса и Кратность всех полюсов равна 1.

По формуле (4) будем иметь:

Тогда:

По формуле Дюамеля получим решение первого заданного уравнения:

.

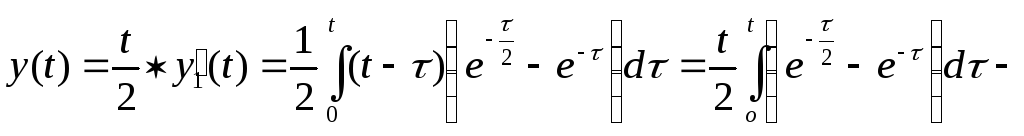
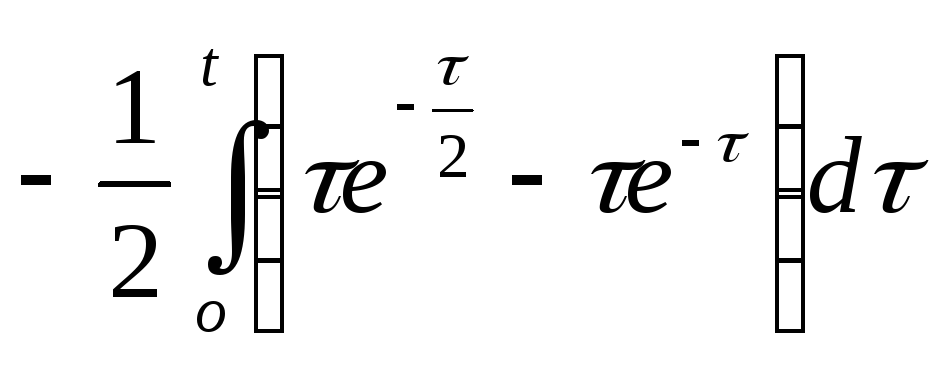После вычисления интегралов и подстановки пределов получим:

Аналогичным образом по формуле Дюамеля получим решение второго уравнения:

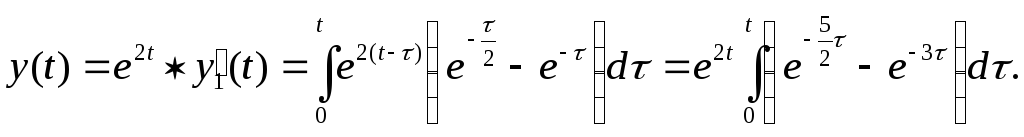
После вычисления интеграла и подстановки пределов получим:

Задача 8. Решить систему дифференциальных уравнений операционным методом.

Пусть , тогда по формуле (2) получим:

Система операторных уравнений будет иметь вид:

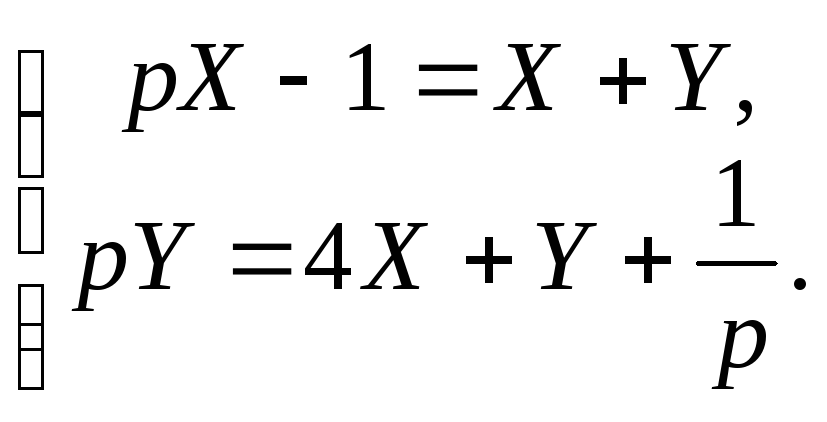
Выразим из первого уравнений и подставим его во второе уравнение системы:

Найдем особые точки данной функции. Для этого приравняем знаменатель к 0:

Получим три простых полюса и

По формуле (4) будем иметь:

Из первого уравнения заданной системы найдем

Проверка:

Библиографический список

Содержание

Введение	1
Задание к курсовой работе	2
Этапы выполнения курсовой работы	2
Приложение А. Образец титульного листа	7
Приложение Б. Образец выполнения курсовой работы	8
Библиографический список	23

22