7. Методы расчёта сложных разветвлённых цепей постоянного тока. Взаимное преобразование схем соединений треугольником и звездой пассивных элементов цепи

Методы расчёта сложных разветвлённых цепей постоянного тока:

1. С помощью уравнений электрического состояния (1 и 2 законы Кирхгофа)

2. Метод наложения

Используется для линейной электрической цепи. Заключается в том, что если цепь подвергается воздействию нескольких источников ЭДС одновременно, то реакция (ток) цепи на эти источники будет равна алгебраической сумме реакций (токов) на каждое воздействие отдельно.

3. Метод контурных токов

В качестве промежуточных переменных выбирают токи, замыкающиеся в каждом контуре и их называют контурными токами. Метод выгоден тогда, когда

4. Метод узлового напряжения

Если цепь имеет 2 узла или путем не сложных преобразований может быть приведена к 2 узлам, то используется метод узлового напряжения.

5. Метод эквивалентного источника

Суть метода эквивалентного генератора состоит в нахождении тока в одной выделенной ветви, при этом остальная часть сложной электрической цепи заменяется эквивалентным ЭДС Е_экв, с её внутренним сопротивлением r_экв. При этом часть цепи, в которую входит источник ЭДС называют эквивалентным генератором или активным двухполюсником, откуда и название метода.

8. Электрические цепи однофазного переменного тока. Переменные ЭДС, напряжения и токи. Цепи синусоидального тока. Основные характеристики синусоидальных электрических величин. Мгновенное, амплитудное и действующее значения. Среднее значение синусоидальной величины.

Переменным называется ток, который изменяется в течение времени по величине или направлению. Переменный ток получил преимущественное распространение в промышленности, что связано с его преимуществами перед постоянным током:

• легко повышается и понижается напряжение с помощью трансформаторов;

• генераторы и двигатели переменного тока проще по устройству, в эксплуатации, надежней и дешевле;

• переменный ток удобнее вырабатывать на электростанциях;

• многие физические явления проявляются только при переменном токе.

• В электрических цепях переменного тока наиболее часто используют синусоидальную форму, характеризующуюся тем, что все токи и напряжения являются синусоидальными функциями времени. Синусоидальная форма тока и напряжения позволяет производить точный расчет электрических цепей с использованием метода комплексных чисел и приближенный расчет на основе метода векторных диаграмм.

Недостатки: в цепях питания потребителей таким током могут происходить перегрузки, вызванные реактивной мощностью потребителей (когда в цепи питания присутствуют индуктивности или емкости); переменный ток приводит к образованию переменных электромагнитных полей, воздействующих на работу различной радиоаппаратуры и др.

Мгновенное значение (ЭДС или напряжения или тока) - значение величины в данный момент времени. обозначается чаще всего маленькими буквами: e, u,i.  

Амплитудное значение  (ЭДС или напряжения или тока) - максимальное значение.

Характеристики синусоидальных функций

Синусоидально изменяющиеся величины характеризуются следующими основными параметрами:

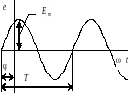
• период Т, [c] - время совершения одного полного колебания синусоидальной величины;

• частота f, [c^-1]=[Гц] - количество периодов, укладывающихся в единицу времени:

.

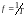В нашей стране частота тока в сети f=50 Гц (достигается вращением роторов в генераторах с частотой вращения n _вр =3000 мин^-1 (об/мин);

• угловая (циклическая) частота изменения тока:

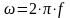, рад/c. Для нашей сети =314 рад/c;

• амплитуда I_m, E_m, U_m - наибольшее значение синусоидальной величины. Амплитудные значения синусоидальных функций являются постоянными величинами, т.е. от времени они не зависят.

• мгновенные значения синусоидальных функций обозначают маленькими буквами: i, e, u. Они являются функциями времени. Зависимость их от времени выражается соотношениями:

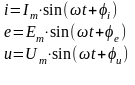
• фаза - аргумент синусоидальной функции (t+) - показывает, какое значение имеет синусоидальная функция в данный момент времени;

• начальная фаза  - показывает, какое значение имеет синусоидальная функция в момент начала отсчета, т.е. при t=0;

Действующее значение переменного тока

Действующим значением I переменного тока называют такое значение постоянного I, который, протекая по сопротивлению R, за время, равное одному периоду Т изменения тока, выделяет в нем такое же количество теплоты Q, что и переменный ток i. Поясним определение на примере:

, где .

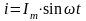После подстановки значения тока i и последующих преобразований получим, что действующее значение переменного тока равно:

.

Аналогичные соотношения могут быть получены также для напряжения и ЭДС:

.

Большинство электроизмерительных приборов измеряют не мгновенные, а действующие значения токов и напряжений.

П од средним значением синусоидально изменяющейся величины понимают ее среднее значение за половину периода:

9. Представления синусоидальных ЭДС, напряжений и токов виде вращающихся векторов и в виде комплексных величин. Комплексные амплитуды синусоидальных ЭДС, напряжения и тока. Оператор поворота комплексной амплитуды и соответствующая векторная диаграмма.

(Нарисовать 3 таких рисунка, над векторами подписать I, U, R на разных рисунках).

Длина отрезка ОА в принятом масштабе равна амплитуде тока (ЭДС, напряжения). Проекция вектора на ось ординат (ОВ) равна мгновенному значению тока (ЭДС, напряжение) в момент времени. При вращении вектора в положительном направлении (т.е. против часовой стрелки) с угловой скоростью в любой момент времени его проекция на ось ординат будет равна соответствующему мгновенному значению тока (ЭДС, напряжение):

i=I_msin(ωt+φ_i) (e=E_msin(ωt+φ_i); u=U_msin(ωt+φ_i))

Любой вектор на плоскости, проведенный из начала координат и изображающий значение ЭДС, напряжения или тока, однозначно определяется точкой, соответствующей концу этого вектора (т. А).

Комплексное число (соответствующее точке ) имеет вещественную (ОС) и мнимую (ОВ) составляющие на комплексной плоскости.

Соответственно формулы для тока, ЭДС и напряжения будут выглядеть так:

I_m= I_me^j𝜓= I_mcos𝜓_i+ jI_msin𝜓_i

E_m= E_me^j𝜓= E_mcos𝜓_i+ jE_msin𝜓_i

U_m= U_me^j𝜓= U_mcos𝜓_i+ jU_msin𝜓_i

j- оператор поворота комплексной амплитуды